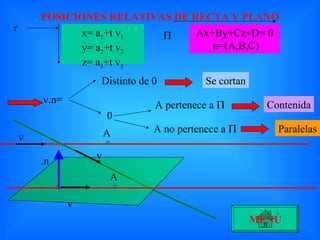
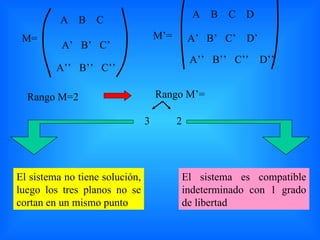
El documento resume conceptos geométricos fundamentales como el punto medio de dos puntos, la simetría de un punto respecto a otro, ecuaciones de rectas y planos, y posiciones relativas de rectas, planos y un plano y una recta. Explica cómo determinar estas propiedades y relaciones mediante el uso de ecuaciones vectoriales, paramétricas y normales.

1. SIMÉTRICO DE UN PUNTO RESPECTO DE UN PUNTO PUNTO MEDIO DE DOS PUNTOS ECUACIONES DE UNA RECTA POSICIONES RELATIVAS DE DOS RECTAS ECUACIONES DE UN PLANO POSICIONES RELATIVAS DE DOS PLANOS POSICIONES RELATIVAS DE TRES PLANOS POSICIONES RELATIVAS DE RECTA Y PLANO Espacio Afín FIN

2. u 1 u 2 u 3 o A X COORDENADAS DEL SIMÉTRICO DE A RESPECTO A X ¿A’? OA’=OA+AA’ OA’=OA+2AX A’ OA’=OA+2(OX-OA) OA’=2OX-OA MENÚ

3. u 1 u 2 u 3 o P M COORDENADAS DEL PTO MEDIO DE DOS PUNTOS P,Q ¿M? OM=OP+PM OM=OP+1/2PQ Q OM=OP+1/2(OQ-OP) OM=1/2(OQ+OP) MENÚ

4. u 1 u 2 u 3 o A v X ¿OX? OX=OA+AX OX=OA+t v ECUACIONES DE UNA RECTA

5. OX=OA+tv : Ecuac.Vectorial (x 1 , x 2 , x 3 )= (a 1 , a 2 , a 3 )+t (v 1 , v 2 , v 3 ) x 1 = a 1 +t v 1 x 2 = a 2 +t v 2 x 3 = a 3 +t v 3 :Ecuac. Paramétricas :Ecuac. Continua Ax+By+Cz-D=0 A’x+B’y+C’z+D=0 ECUACIONES DE UNA RECTA t= x 1 - a 1 v 1 t= x 2 – a 2 v 2 t= x 3 – a 3 v 3 x 1 - a 1 = x 2 – a 2 = x 3 – a 3 V 1 v 2 v 3

6. PROBLEMAS PROPUESTOS : 1.- Determinar las ecuaciones de la recta que pasa por dos puntos dados 2.- Condiciones de incidencia punto recta 3.- Condiciones para que tres puntos estén alineados MENÚ

7. POSICIONES RELATIVAS DE DOS RECTAS SE CRUZAN SON PARALELAS SE CORTAN COINCIDENTES

8. POSICIONES RELATIVAS DE DOS RECTAS x 1 = a 1 +t v 1 x 2 = a 2 +t v 2 x 3 = a 3 +t v 3 r x 1 = a’ 1 +s v’ 1 x 2 = a’ 2 +s v’ 2 x 3 = a’ 3 +s v’ 3 r’ a 1 +t v 1 = a’ 1 +s v’ 1 a 2 +t v 2 = a’ 2 +s v’ 2 a 3 +t v 3 = a’ 3 +s v’ 3 t v 1 -s v’ 1 = a’ 1 -a 1 t v 2 -s v’ 2 = a’ 2 -a 2 t v 3 -s v’ 3 = a’ 3 -a 3 v 1 v’ 1 v 2 v’ 2 v 3 v’ 3 M= Rango M= 2 Rango M’= 3 Se cruzan 2 Se cortan 1 Rango M’= 2 1 Paralelas Coincidentes MENÚ

9. u 1 u 2 u 3 o A X ECUACIONES DE UN PLANO OX=OA+AX AX=t u+ s v OX=OA+ t u+ sv v u

10. OX=OA+tu+sv: Ecuac.Vectorial (x 1 , x 2 , x 3 )= (a 1 , a 2 , a 3 )+t (u 1 , u 2 , u 3 )+ s (v 1 , v 2 , v 3 ) x 1 = a 1 +t u 1 +s v 1 x 2 = a 2 +t u 2 +s v 2 x 3 = a 3 +t u 3 +s v 3 :Ecuac. Paramétricas x 1 - a 1 u 1 v 1 x 2 – a 2 u 2 v 2 x 3 – a 3 u 3 v 3 Ax+By+Cz+D=0 =0 :Ecuac. General

11. u 1 u 2 u 3 o A X ECUACIÓN NORMAL DE UN PLANO n AX= 0 n (OX-OA)=0 n Si sup. Una base ortonormal: n 1 (x-a 1 )+ n 2 (y-a 2 )+ n 3 (z-a 3 )=0 n 1 x+ n 2 y+ n 3 z+(-n 1 a 1 -n 2 a 2 -n 3 a 3 )=0 Ax+By+Cz+D=0

12. PROBLEMAS PROPUESTOS : 1.- Determinar las ecuaciones del plano determinado por tres puntos no alineados 2.- Condiciones de incidencia punto plano 3.- Condiciones para que cuatro puntos sean coplanarios

13. u 1 u 2 u 3 o A X ECUACIÓN DE UN PLANO POR 3 PTOS OX=OA+AX AX=t AB+ s AC OX=OA+ t AB+ sAC B C MENÚ

14. POSICIONES RELATIVAS DE DOS PLANOS

15.  : Ax+By+Cz+D=0  : A’x+B’y+C’z+D’=0 M= M’= Rango M= 2 Rango M’= 2 Se cortan 1 Rango M’= 2 1 Paralelos Coincidentes MENÚ A B C A’ B’ C’ A B C D A’ B’ C’ D’

16. POSICIONES RELATIVAS DE RECTA Y PLANO x= a 1 +t v 1 y= a 2 +t v 2 z= a 3 +t v 3 r Ax+By+Cz+D= 0 n=(A,B,C)  Distinto de 0 Se cortan 0 Paralelas Contenida v.n= A A pertenece a  A no pertenece a  A MENÚ .n v v v

17.  : Ax+By+Cz+D=0  : A’x+B’y+C’z+D’=0 M= M’=  A’’x+B’’y+C’’z+D’’=0 POSICIONES RELATIVAS DE TRES PLANOS A B C A’ B’ C’ A’’ B’’ C’’ A B C D A’ B’ C’ D’ A’’ B’’ C’’ D’’

18. Rango M= 3 2 I Rango M’=3 Rango M’=3 Rango M’=2 Rango M’=2 Rango M’=1

19. Rango M=3 Se cortan en un pto

20. Rango M=2 Rango M’= El sistema no tiene solución, luego los tres planos no se cortan en un mismo punto M= M’= 3 2 El sistema es compatible indeterminado con 1 grado de libertad A B C A’ B’ C’ A’’ B’’ C’’ A B C D A’ B’ C’ D’ A’’ B’’ C’’ D’’

21. Rango M=2 Rango M’= El sistema no tiene solución, luego los tres planos no se cortan en un mismo punto Dos planos paralelos y uno secante Secantes dos a dos 3

22. Rango M=2 Rango M’= M= M’= 2 El sistema es compatible indeterminado con 1 grado de libertad A B C A’ B’ C’ A’’ B’’ C’’ A B C D A’ B’ C’ D’ A’’ B’’ C’’ D’’

23. Rango M=1 Rango M’= El sistema no tiene solución, luego los tres planos no se cortan en un mismo punto M= M’= 2 1 El sistema es compatible indeterminado con 2 grado de libertad A B C A’ B’ C’ A’’ B’’ C’’ A B C D A’ B’ C’ D’ A’’ B’’ C’’ D’’

24. Rango M=1 Rango M’= El sistema no tiene solución, luego los tres planos no se cortan en un mismo punto Tres planos paralelos Dos planos paralelos y un coincidente 2

25. Rango M=1 Rango M’= El sistema tiene solución, con dos grados de libertad Tres planos coincidentes 1

26. HAZ DE PLANOS POR UNA RECTA r= Ax+By+Cz+D=0 A’x+B’y+C’z+D’=0 Ax+By+Cz+D=0 A’x+B’y+C’z+D=0 A’’x+B’’y+C’’z+D’’=0 El sistema tiene solución con un grado de libertad. A’’x+B’’y+C’’z+D’’=0 Es combinación lineal de las otras dos A’’x+B’’y+C’’z+D’’=  Ax+By+Cz+D)+  A’x+B’y+C’z+D’)=0 MENÚ