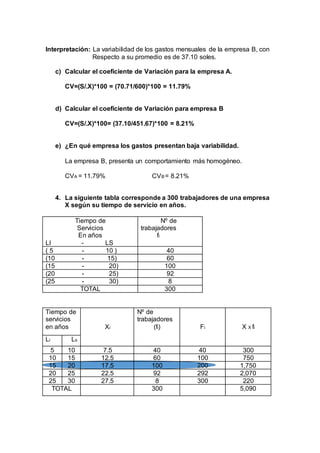
Este documento presenta varios ejercicios estadísticos que involucran el cálculo de medidas como la media, mediana, moda, desviación estándar y coeficientes de variación para diferentes conjuntos de datos. Los datos se refieren a tiempo de navegación en internet, ventas mensuales, gastos de empresas y tiempo de servicio de trabajadores. Para cada conjunto de datos se piden calcular y interpretar diferentes medidas estadísticas.

1. ACTIVIDAD DE APRENDIZAJE II
1. Los siguientes datos corresponden a 10 cibernautas según el
tiempo en minutos que pasan navegando en internet:
Xi= 35, 45, 50, 55, 35, 40, 55, 60, 42,45
Solución
Calcular e interpretar
a) La media
X= = (35+45+50+55+35+40+55+60+42+45+)/ 10 = 46.2
Interpretar: Los cibernautas tienen un tiempo promedio de
navegación en internet de 46.2 minutos.
b)La mediana
Xi = 35, 45, 50, 55, 35, 40, 55, 60, 42,45
Ordenamos los datos
35
35
40
42 Hallamos la posición de la Mediana= (n+1)
45 Posición de Mediana = (10+1)/2 = 5.5
45
50 Me= (45+45)/2= 45
55
55 Interpretación: El 50% de los cibernautas en internet
60 tienen un tiempo de navegación en
Internet mayor o igual a 45 minutos y
el
50% restante menores o iguales a 45
Minutos.
c) La moda
El tiempo de navegación de los cibernautas es trimodal pues existen tres
tiempos que se repiten más 35 min, 45 min y 55min.

2. d) La desviación estándar
Xi = 35, 45, 50, 55, 35, 40, 55, 60, 42,45
2 2 2
α = √1 Σ(푋푖 − 푋) 2 = (35-46.2) + (45-46.2) +…+ (45-46.2)
n / (10-1)= 8.63 minutos.
Interpretación:
La variabilidad de los tiempos de navegación con respecto
a su promedio es de 8.63 minutos.
e) Coeficiente de Variación CV= (S/ X) *100=
(8.63/46.2)*100=18.68%
Interpretar: Los tiempos de navegación presentan un
Comportamiento homogéneo CV es menor al 33%
f) Coeficiente de Asimetría
As= 3(X-Me)/S = 3(46.2-45)/ 8.63 = 0.42
Interpretación: Se indica que los tiempos de navegación presenta una
asimetría positiva, es decir la mayor parte de los datos son menores que
el promedio.
2. Los siguientes datos corresponden a las ventas mensuales en
dólares realizadas en el año 2006 por una empresa de productos
hidrobiológicos:
Xi= Ventas Mensuales (en dólares)
2,000 solución:
2,500 a) La Mediana
2,500 Hallamos la posición de la Mediana= (n+1)/2
2,500 Posición de la Mediana= (12+1)/2 = 6.5
2,500
2,700
2,800 Me= (2,700+2,800)/2 = 2,750
3,000
4,000 Interpretar: El 50% de los meses tiene una
4,200 venta mensual máxima de
4,500 2,750 dólares.
5,000

3. b. La Media
XΣ fi= 1 = 3,183.3
n
c. La Moda
Interpretación.- El monto de venta
mensual que más se registra es de 2,500
3. En dos empresas de telecomunicaciones se dan los siguientes
gastos mensuales en soles (de los últimos 6 meses) en material y
mantenimiento informático:
MESES OCTUBRE NOV. DIC. ENERO FEB. MARZO
EMP. A 500 550 600 700 650 600
EMP. B 450 480 500 460 420 400
Solución
Se pide
a) Calcular la desviación estándar para la zona A.
Σ X1
X= f=1 =600
n
α =√1 Σ(푋1 − 푋)2 − 70.71
n
Interpretación: La variabilidad de los gastos mensuales de la empresa A con
respecto a su promedio es de 70.71 soles.
b) Calcular la desviación estándar para la empresa B
- n
X= Σ X1 = 451.67
F=1
n
2
α= √1 Σ(푋푖 − 푋 = 37.10
n

4. Interpretación: La variabilidad de los gastos mensuales de la empresa B, con
Respecto a su promedio es de 37.10 soles.
c) Calcular el coeficiente de Variación para la empresa A.
CV=(S/.X)*100 = (70.71/600)*100 = 11.79%
d) Calcular el coeficiente de Variación para empresa B
CV=(S/.X)*100= (37.10/451.67)*100 = 8.21%
e) ¿En qué empresa los gastos presentan baja variabilidad.
La empresa B, presenta un comportamiento más homogéneo.
CVA = 11.79% CVB = 8.21%
4. La siguiente tabla corresponde a 300 trabajadores de una empresa
X según su tiempo de servicio en años.
Tiempo de
Servicios
En años
LI - LS
Nº de
trabajadores
fi
( 5 - 10 ) 40
(10 - 15) 60
(15 - 20) 100
(20 - 25) 92
(25 - 30) 8
TOTAL 300
Tiempo de
servicios
en años
Xi
Nº de
trabajadores
(fi)
Fi
X X fi
Li Ls
5 10 7.5 40 40 300
10 15 12.5 60 100 750
15 20 17.5 100 200 1,750
20 25 22.5 92 292 2,070
25 30 27.5 8 300 220
TOTAL 300 5,090

5. Solución
Se pide:
a) Calcular el promedio e interpretar.
_ n
X = Σ Xi f1 = 5,090/ 300 = 16.97
i-1----------
n
Interpretación: Los trabajadores de la empresa tienen un tiempo promedio
de 16.97 años de servicio.
b) Calcular la Mediana e interpretar:
n
Me= Li +A 2 – F1-1 = 15+5(150-100/100) = 17.5
f
Interpretación: El 50% de los trabajadores tienen un tiempo de servicio
mayor o igual a 17.5 años y el restante 50% de trabajadores tienen
tiempo de servicios menor o iguales a 17.5 años.
c) Calcular la moda e interpretar:
Mo= Li + A A1 = 15+5(40/40+8) = 19.17
A1 + A2
D1 = 100-60 = 40
D2 = 100-92 = 8
Interpretación: El tiempo de servicio más frecuente en la empresa es de
19.17 años.

6. 5. Un dueño de una fábrica considera que si la producción de una
máquina que tiene muchos años de vida tiene una producción
heterogénea en estos últimos 5 días tendrá que darle de baja. Los
resultados se muestran a continuación en números de unidades:
X = 140
127
125
148
146
Solución:
X = Σ X1 = 137.2
F = 1
n
n 2
α = 1/n Σ (Xi- X) = 10.66
CV= (S/. X)* 100 = 10.66/137.2 = 7.77%
Interpretación: Un coeficiente de variación igual a 7.77 % nos indica.
6. Un inversor posee una cartera compuesta por acciones de dos
entidades financieras A y B. La composición de esta cartera, así
como la cotización de las acciones se ha modificado a lo largo del
año, disponiéndose de la siguiente información.
Artículos Cotización (Euros) Nº de acciones
15 de
Enero
15 de
Febrero
15 de
Marzo
15 de
Enero
15 de
Febrero
15 de
Marzo
Entidad
A
17.2 18.9 16.4 75 90 100
Entidad
B
12.3 9.4 11.5 125 110 100

7. a) Calcular e interpretar el índice de precios simple para la entidad A
del 15 de marzo respecto al 15 de febrero.
Cálculo del índice:
1p = Pn = 16.40 x 100 = 86.5
Po 18.96
b) Calcular e interpretar el índice de cantidad simple para la entidad B
del 15 de marzo respecto del 15 de enero.
Cálculo de índice:
1q = q n = 100 x 100 = 80.0
qo 125
c) Calcular e interpretar el índice de valor simple para la entidad B del
15 de febrero al 15 de enero
Cálculo del índice:
1p = pn qn = 18.96*(90) = 1.98418605
P0 q0 17.2*(50)
d) Calcular e interpretar el índice ponderado de precios del 15 de
marzo con respecto al 15 de enero por el método de Laspeyres.
Cálculo de índice
I PL = Σ p1q0 X 100 = 12.3 x 75 + 9.4 x 90 + 11.5 x 100 x 100
Σ p0q0 17.2 x 75 + 18.9 x 90 + 16.4 x 100
I PL = 78.223%