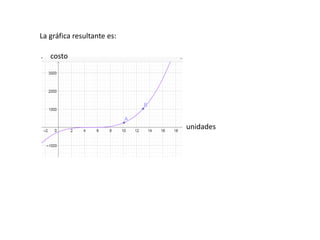
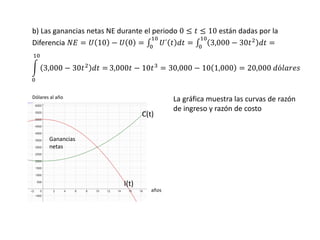
El documento presenta un problema de aplicación de integrales para calcular la rentabilidad de una máquina a lo largo del tiempo. La rentabilidad comienza a disminuir después de 10 años, y las ganancias netas de la máquina durante los primeros 10 años son de $20,000 dólares. También presenta un problema para calcular el aumento en el costo total de producción cuando el nivel de producción aumenta de 10 a 13 unidades, el cual es de $774 dólares.

1. INTEGRALES. PROBLEMAS DE APLICACIÓN.
1. Cuando una máquina tiene t años, genera ingresos a razón de:
𝐼´ 𝑡 = 5,000 − 20𝑡2
dólares al año
y los costos de operación se acumulan a razón de:
C´ 𝑡 = 2,000 + 10𝑡2
dólares al año
a) ¿Cuántos años transcurren antes de que la rentabilidad de la máquina
comience a disminuir?
b) Calcule las ganancias netas generadas por la máquina, durante el periodo
Indicado en el inciso anterior.
a) La utilidad asociada a la máquina después de t años de funcionamiento es:
U(t) = I(t) – C(t), y la tasa de rentabilidad es:
𝑈´ 𝑡 = 𝐼´ 𝑡 − 𝐶´ 𝑡 = (5,000 − 20𝑡2
) − (2,000 + 10𝑡2
) =
5,000 − 20𝑡2 − 2,000 − 10𝑡2 = 3,000 − 30𝑡2
La rentabilidad comienza a disminuir cuando 𝑈´ 𝑡 = 0
entonces: 3,000 − 30𝑡2
= 0 −30𝑡2
= − 3000
𝑡2
= 3000/30 = 100 Entonces: 𝑡 = 10 años

2. b) Las ganancias netas NE durante el periodo 0 ≤ 𝑡 ≤ 10 están dadas por la
Diferencia 𝑁𝐸 = 𝑈 10 − 𝑈 0 = 𝑈´ 𝑡 𝑑𝑡 = 3,000 − 30𝑡2
𝑑𝑡 =
10
0
10
0
3,000 − 30𝑡2
𝑑𝑡 =
10
0
3,000𝑡 − 10𝑡3
= 30,000 − 10 1,000 = 20,000 𝑑ó𝑙𝑎𝑟𝑒𝑠
Dólares al año
años
C(t)
I(t)
La gráfica muestra las curvas de razón
de ingreso y razón de costo
Ganancias
netas

3. 2. En una fábrica, el costo marginal es 6(𝑞 − 5)2 dólares la unidad cuando el nivel de
producción es q unidades. ¿En cuánto aumentará el costo de fabricación total, si el
nivel de producción sube de 10 a 13 unidades?
Solución:
El costo por unidad es la integral del costo marginal en el intervalo 10 ≤ 𝑞 ≤ 13
6(𝑞 − 5)2
𝑑𝑞 =
6 𝑞 − 5 3
3
= 2(𝑞 − 5)3
13
10
Sustituyendo q en el intervalo indicado: 2[(13 − 5)3
- (10 − 5)3
] =
2[(8)3
- (5)3
] =2[512- 125] = 2[387] = 774 𝑑ó𝑙𝑎𝑟𝑒𝑠

4. La gráfica resultante es:
costo
unidades