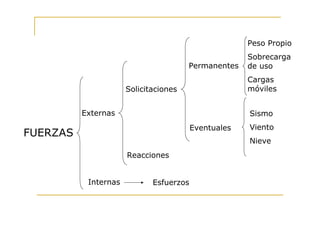
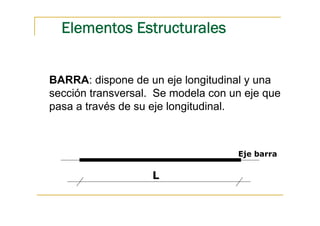
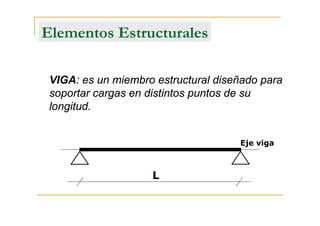
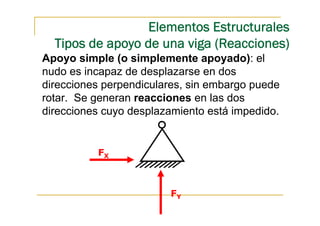
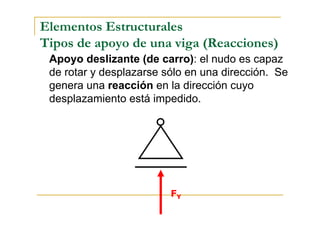
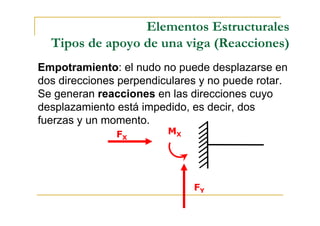
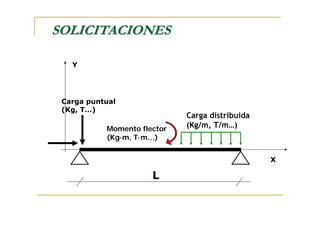
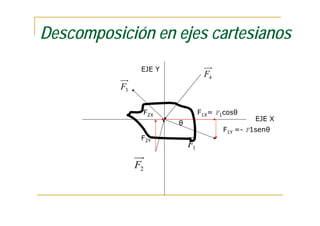
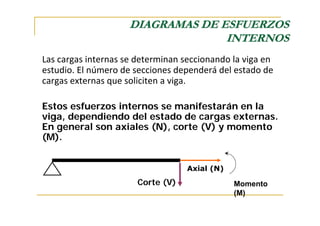
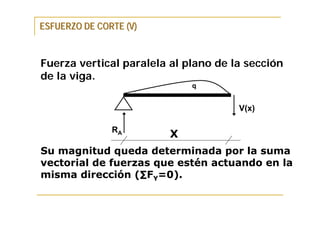
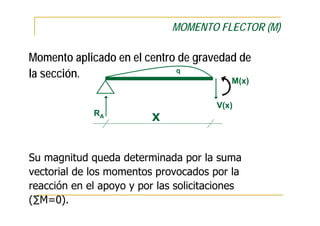
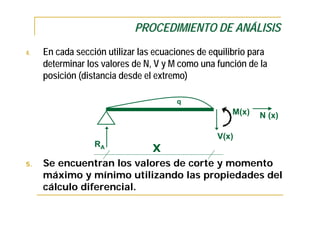
Este documento presenta conceptos fundamentales sobre el análisis estructural de vigas isostáticas. Define términos como ingeniería estructural, fuerzas externas, internas y de reacción. Explica los principios del análisis estructural, tipos de apoyos, elementos estructurales y diagramas de esfuerzos internos. Finalmente, describe el procedimiento de análisis estructural que incluye determinar reacciones, seccionar la viga y analizar cada sección mediante el diagrama de cuerpo libre.

1. UNIVERSIDAD DE SANTIAGO DE CHILE
Dpto. de Ingeniería en Obras Civiles
Construcción Civil
ESTRUCTURAS
Segundo Semestre 2008
Prof. Alejandro Torres F.
atorres@usach.cl

2. Cálculo de Estructuras Isostáticas
Conceptos Preliminares
Ingeniería
Estructural:
disciplina cuyo
objetivo es el análisis,
planificación, diseño,
construcción y
mantenimiento de
sistemas
estructurales.

3. Cálculo de Estructuras Isostáticas
Conceptos Preliminares
Principios del Análisis Estructural
1. La vinculación de los sistemas estructurales al
terreno de fundación o a otros sistemas, será
tal que éstos permanecerán sin movimientos
de cuerpo rígido cuando sobre él actúe una
fuerza estática.
2. Las fuerzas que participan en estos tipos de
sistemas estructurales estarán gobernadas
por las leyes del equilibrio estático.

4. Cálculo de Estructuras Isostáticas
Conceptos Preliminares
Principios del Análisis Estructural
3. El conjunto de las deformaciones de una
estructura debe satisfacer condiciones de
compatibilidad geométrica. Debe existir
continuidad de los elementos estructurales y
sus conexiones.
4. Las fuerzas y deformaciones están
relacionadas por la ley tensión-deformación
que caracteriza al material estructural.

5. Definición de Fuerzas
FUERZA EXTERNA (Solicitaciones): es la
fuerza que solicita a una estructura. Pueden ser
fuerzas verticales, horizontales, inclinadas y
momentos.
REACCIÓN: es la fuerza con que el material
sobre el cual se apoya la estructura, responde
ante las fuerzas transmitidas por ésta.
FUERZA INTERNA: es la fuerza que se
genera dentro del cuerpo como respuesta a
las fuerzas externas y a las reacciones.

6. Definición de Fuerzas
FUERZA PUNTUAL: es una fuerza que se
concentra en una superficie suficientemente
pequeña como para ser considerada un punto.
FUERZA DISTRIBUIDA
Lineal: es una fuerza que está aplicada sobre
una superficie suficientemente delgada como
para ser considerada una línea (peso propio de
una viga).
Distribuida: es la fuerza que está aplicada
sobre una superficie (peso propio de una losa).

7. Definición de Fuerzas
Carga Muerta: es la carga externa producida
por estados externos que no sufrirán
modificación en el tiempo (peso propio,
sobrecarga de uso, muebles, etc.).
Carga Viva: es la carga externa producida
por solicitaciones eventuales (sismo, viento,
nieve, etc.).

8. Peso Propio
Sobrecarga
Permanentes de uso
Cargas
Solicitaciones móviles
Externas Sismo
Eventuales Viento
FUERZAS
Nieve
Reacciones
Internas Esfuerzos

9. Elementos Estructurales
BARRA: dispone de un eje longitudinal y una
sección transversal. Se modela con un eje que
pasa a través de su eje longitudinal.
Eje barra
L

10. Elementos Estructurales
VIGA: es un miembro estructural diseñado para
soportar cargas en distintos puntos de su
longitud.
Eje viga
L

11. Elementos Estructurales
Tipos de apoyo de una viga (Reacciones)
Apoyo simple (o simplemente apoyado): el
nudo es incapaz de desplazarse en dos
direcciones perpendiculares, sin embargo puede
rotar. Se generan reacciones en las dos
direcciones cuyo desplazamiento está impedido.
FX
FY

12. Elementos Estructurales
Tipos de apoyo de una viga (Reacciones)
Apoyo deslizante (de carro): el nudo es capaz
de rotar y desplazarse sólo en una dirección. Se
genera una reacción en la dirección cuyo
desplazamiento está impedido.
FY

13. Elementos Estructurales
Tipos de apoyo de una viga (Reacciones)
Empotramiento: el nudo no puede desplazarse en
dos direcciones perpendiculares y no puede rotar.
Se generan reacciones en las direcciones cuyo
desplazamiento está impedido, es decir, dos
fuerzas y un momento.
FX MX
FY

14. SOLICITACIONES
Y
Carga puntual
(Kg, T…)
Carga distribuida
Momento flector (Kg/m, T/m…)
(Kg·m, T·m…)
X
L

15. Descomposición en ejes cartesianos
EJE Y
F4
F3
F2X F1X= F1cosθ
EJE X
θ
F1Y =- F1senθ
F2Y
F1
F2

16. EQUILIBRIO
ESTÁTICO
Cuando un cuerpo está en reposo o se
mueve con velocidad constante (esto es, su
aceleración a=0), se dice que este cuerpo
está en equilibrio.
El equilibrio requiere que todas las fuerzas que
actúan sobre la partícula formen una resultante
de fuerza nula.

17. EQUILIBRIO ESTÁTICO
Es decir, considerando la segunda ley del
movimiento de Newton F = m·a, cuando el
cuerpo se mueve a velocidad constante o está
en reposo a=0.
Por lo tanto, en condición de equilibrio estático,
F=m·a=0.

18. EQUILIBRIO ESTÁTICO
Condiciones de equilibrio, las ecuaciones
fundamentales de la estática:
∑FX = 0 ∑F y = 0
∑M = 0
Estas ecuaciones que definen el equilibrio estático,
son condiciones necesarias y suficientes para
reflejar esta situación.

19. Diagrama de cuerpo libre
Para aplicar las ecuaciones de equilibrio, se
deben considerar todas las fuerzas conocidas
y desconocidas que actúan sobre un cuerpo.
La manera más simple de efectuar este análisis es
a través de la construcción del diagrama de
cuerpo libre.
Este diagrama es un esquema simple que muestra el
elemento libre de su entorno con todas las cargas
que lo solicitan.

20. Diagrama de cuerpo libre
Procedimiento
1. Se debe dibujar el cuerpo o elemento estructural libre de
su entorno.
2. Indicar sobre este esquema, todas las fuerzas conocidas
y desconocidas, las que pueden ser activas (tienden a
poner el cuerpo en movimiento), o fuerzas reactivas (que
son resultado de las restricciones o apoyos que tienden a
prevenir el movimiento.
3. Las fuerzas conocidas deberán rotularse con sus
magnitudes y direcciones; las desconocidas se definirán
positivas y su magnitud se representa mediante una letra
(incógnita).

21. Sistemas estructurales
longitudinales
Elementos básicos:
Elementos lineales rectos.
Sección pequeña respecto a
su longitud.
Esfuerzos internos
Axiales (compresión o
tracción)
Flexión
Corte

22. Fuerzas internas en elementos estructurales
Análogamente al caso de las cargas
externas (reacciones y solicitaciones),
también los cuerpos están caracterizados
por esfuerzos internos.
El diseño de cualquier elemento estructural,
requiere estudiar estos esfuerzos internos, para
asegurarse de que el material puede resistir las
cargas externas.

23. DIAGRAMAS DE ESFUERZOS
INTERNOS
Las cargas internas se determinan seccionando la viga en
estudio. El número de secciones dependerá del estado de
cargas externas que soliciten a viga.
Estos esfuerzos internos se manifestarán en la
viga, dependiendo del estado de cargas externas.
En general son axiales (N), corte (V) y momento
(M).
Axial (N)
Corte (V) Momento
(M)

24. Esfuerzos internos en vigas
Si se considera un diagrama de cuerpo libre de un
trozo de viga (entre un apoyo y una sección
intermedia cualquiera) el conjunto total de las
fuerzas actuantes, es decir, solicitaciones, reacciones
y esfuerzos internos deben estar en equilibrio.

25. ESFUERZO DE CORTE (V)
Fuerza vertical paralela al plano de la sección
de la viga.
q
V(x)
RA
X
Su magnitud queda determinada por la suma
vectorial de fuerzas que estén actuando en la
misma dirección (∑FY=0).

26. MOMENTO FLECTOR (M)
Momento aplicado en el centro de gravedad de
la sección. q
M(x)
V(x)
RA
X
Su magnitud queda determinada por la suma
vectorial de los momentos provocados por la
reacción en el apoyo y por las solicitaciones
(∑M=0).

27. DIAGRAMAS DE MOMENTO Y CORTE EN
FLEXIÓN
Al efectuar cortes en diferentes secciones
características de la viga, se puede encontrar
la expresión de V y M para esos puntos.
El dibujo de la distribución de los valores
calculados en cada sección de la viga, se
denomina diagrama.

28. OBJETIVO DE LOS DIAGRAMAS
Entregar la ubicación y el valor de los esfuerzos
máximos y mínimos.
Indicar el signo de éstos.
Ver la forma cómo varían a lo largo de la viga.

29. PROCEDIMIENTO DE ANÁLISIS
1. Determinar las reacciones en los apoyos.
2. Seccionar la viga en tantas partes como cambios en
el estado de cargas tenga la viga.
3. Analizar una a una las secciones determinadas en
el punto anterior comenzando por la menos
cargada, trazando el diagrama de cuerpo libre de
cada sección.

30. PROCEDIMIENTO DE ANÁLISIS
4. En cada sección utilizar las ecuaciones de equilibrio para
determinar los valores de N, V y M como una función de la
posición (distancia desde el extremo)
q
M(x) N (x)
V(x)
RA
X
5. Se encuentran los valores de corte y momento
máximo y mínimo utilizando las propiedades del
cálculo diferencial.

31. RECOMENDACIONES (Diagrama de corte)
1. El diagrama comienza con el valor de la reacción en el
primer apoyo de la izquierda y termina con el valor de la
reacción de la derecha.
2. En los tramos donde no hay cargas el valor se
mantiene constante, por lo tanto el diagrama es
horizontal.
3. Bajo las cargas puntuales el diagrama no es continuo y
se produce un salto equivalente al valor de la carga.

32. RECOMENDACIONES (Diagrama de corte)
4. Bajo cargas uniformemente distribuidas, el diagrama
varía linealmente.
5. Bajo cargas variables, el diagrama varía en un
grado más que el de la carga. Así, para una
variación lineal de la carga (carga triangular) el
diagrama varía en forma cuadrática.
6. Cuando el diagrama corta el eje de la viga,
generalmente corresponde a un máximo del
momento.

33. RECOMENDACIONES (Diagrama de momento)
1. Identifique los puntos donde el momento es nulo:
- En vigas simplemente apoyadas, en ambos apoyos.
- En cada rótula interna.
- En vigas en voladizo, en su extremo libre.
2. El diagrama de momentos es continuo, solo
presenta saltos cuando hay aplicado un momento
en un punto.
3. En los tramos donde no hay cargas, el diagrama varía en
forma lineal.

34. RECOMENDACIONES (Diagrama de momento)
4. Bajo cargas variables, el diagrama varía en dos
grados más que el de la carga.
5. El diagrama presenta un máximo cuando el
diagrama de corte presenta un punto nulo (es
cero).