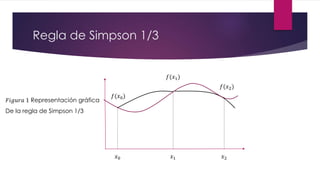
La regla de Simpson 1/3 aproxima el área bajo una curva dividiéndola en parábolas y sumando sus áreas. Utiliza tres puntos por parábola, incluyendo un punto medio. Esto permite aproximar la función por un polinomio de segundo grado entre cada par de puntos. La fórmula resultante para calcular la integral divide la suma de los valores de la función en los tres puntos entre el número de subdivisiones.

1. Regla de Simpson 1/3
CLASE 13
19-JULIO-2014

2. Regla de Simpson 1/3
 La regla de Simpson 1/3 resulta cuando en la ecuación de la integral
 𝑓(x) es reemplazado por un polinomio de Newton-Gregory de segundo orden (parábola). En
este método se tienen tres puntos por cada parábola. Los limites de integración corresponden a
dos de los tres puntos que forman la parábola. El tercer punto es el valor medio de los limites de
integración. La figura 1 muestra la aproximación a la función 𝑓(𝑥) por medio de una parábola.
𝐼 =
𝑎
𝑏
𝑓 𝑥 𝑑𝑥 =
𝑎
𝑏
𝑓2 𝑥 𝑑𝑥 … … … … … (1)

3. Regla de Simpson 1/3
𝑓(𝑥0)
𝑓(𝑥1)
𝑓(𝑥2)
𝑥0 𝑥1 𝑥2
𝐹𝑖𝑔𝑢𝑟𝑎 1 Representación gráfica
De la regla de Simpson 1/3

4. Regla de Simpson 1/3
 Para obtener la formula de integración, se sustituye el polinomio de
Newton Gregory en diferencias progresivas de segundo orden y se realiza
la integración.
𝑎
𝑏
𝑓 𝑥 𝑑𝑥 =
𝑥1
𝑥2
𝑓 𝑥 𝑑𝑥 =
𝑥1
𝑥2
𝑓(𝑥0) + 𝐾∆𝑓 𝑥0 +
𝐾2 − 𝐾
2
∆2
𝑓(𝑥0) 𝑑𝑥 … … (2)
=
0
2
ℎ 𝑓(𝑥0) + 𝐾∆𝑓 𝑥0 +
𝐾2
− 𝐾
2
∆2 𝑓(𝑥0) 𝑑𝐾 … … (3)

5. Regla de Simpson 1/3
= ℎ 𝐾𝑓 𝑥0 +
𝐾2
2
∆𝑓 𝑥0 +
𝐾3
6
−
𝐾2
4
∆2
𝑓 𝑥0
0
2
… … . (4)
= ℎ 2𝑓 𝑥0 + 2∆𝑓 𝑥0 +
1
3
∆2
𝑓 𝑥0 … … . (5)
= ℎ 2𝑓 𝑥0 + 2 𝑓 𝑥1 − 𝑓 𝑥0 +
1
3
𝑓 𝑥2 − 2𝑓 𝑥1 + 𝑓 𝑥0 … … . (6)
= ℎ
6𝑓 𝑥0 + 6𝑓 𝑥1 − 6𝑓 𝑥0 + 𝑓 𝑥2 − 2𝑓 𝑥1 + 𝑓 𝑥0
3
… … . (7)

6. Regla de Simpson 1/3
𝑰 =
𝒉
𝟑
𝒇 𝒙 𝟎 + 𝟒𝒇 𝒙 𝟏 + 𝒇 𝒙 𝟐 … … . (𝟖)

7. Regla de Simpson 1/3
 Ejemplo 1
 Evalué la integral con el uso de la regla de Simpson 1/3 y compare el
resultado con el valor analítico.

0
𝜋
8 + 5𝑠𝑒𝑛 𝑥 𝑑𝑥 = 35.1328

8. Regla de Simpson 1/3
 Solución
 La integral analítica es:

0
𝜋
8 + 5𝑠𝑒𝑛 𝑥 𝑑𝑥 = 35.1328
 La solución numérica es:
 𝐼 = 𝑏 − 𝑎
𝑓 𝑥0 +4𝑓 𝑥1 +𝑓 𝑥2
3𝑛

9. Regla de Simpson 1/3
 Solución
 Recordemos que 𝑓 𝑥 = 8 + 5𝑠𝑒𝑛 𝑥 , con 𝑛 = 2
 𝑓 𝑥0 = 𝑓 0 = 8
 𝑓 𝑥1 = 𝑓 𝜋/2 = 8 + 5 1 = 13
 𝑓 𝑥2 = 𝑓 𝜋 = 8

10. Regla de Simpson 1/3
 Solución
 𝐼 = 𝜋 − 0
8+4 13 +8
6
= 35.6048
 𝐸 𝑣 =
35.1328−35.6048
35.1328
100 = 1.3435%