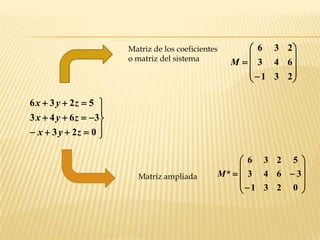
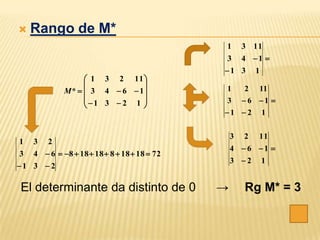
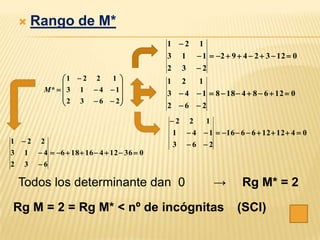
Este documento describe los sistemas de ecuaciones lineales y los métodos para resolverlos. Explica que un sistema puede ser compatible o incompatible dependiendo de si el rango de la matriz de coeficientes es igual o no al rango de la matriz ampliada. También describe los métodos de Cramer y Gauss para resolver sistemas compatibles determinados e indeterminados respectivamente.

1. SISTEMAS DE
ECUACIONES LINEALES
(S. E. L.)

2.  Dado un sistema de ecuaciones lineales
podremos sacar dos matrices:
M La matriz de los coeficientes o
matriz del sistema
M* La matriz ampliada que incluye
además los términos independientes

3. Matriz de los coeficientes  6 3 2
o matriz del sistema  
M   3 4 6
  1 3 2
 
6 x  3 y  2z  5 

3 x  4 y  6 z  3
 x  3 y  2z  0 
 6 3 2 5 
 
Matriz ampliada M*   3 4 6  3
1 3 2 0 
 

4. TEOREMA DE ROUCHÉ-FRÖBENIUS
 Si Rg M = Rg M* el sistema es compatible y
tiene solución
 Si Rg M ≠ Rg M* el sistema es incompatible
y no tiene solución

5. CLASIFICACIÓN DE LOS SISTEMAS
 Si Rg M = Rg M* = nº de incógnitas (SCD)
Sistema compatible determinado, tiene 1 solución
Método de Cramer
 Si Rg M = Rg M* < nº de incógnitas (SCI)
Sistema compatible indeterminado, tiene ∞
soluciones
Método de Gauss
 Si Rg M ≠ Rg M* (SI)
Sistema incompatible, no tiene solución

6. SISTEMAS HOMOGÉNEOS
 Los sistemas homogéneos tienen como término
independiente 0 en todas sus ecuaciones
2 x  3 y  5z  0 

3 x  4 y  2z  0 
 x  3 y  2 z  0

 Se tratan de sistemas compatibles, siempre
tienen solución Rg M = Rg M*
 Si la solución es única se trata de la solución
trivial (0, 0, 0)

7. MÉTODO DE CRAMER
 Se aplica en sistemas compatibles
determinados (SCD) con 1 solución
Rg M = Rg M* = nº de incógnitas
x  3 y  2 z  11   1 3 2   1 3 2 11 
    
3 x  4 y  6 z  1 M   3 4  6 M *   3 4  6  1
  1 3  2 1 3  2 1 
 x  3 y  2z  1     

8.  Rango de M
 1 3 2 
 
M   3 4  6
  1 3  2
 
1 3 2
3 4  6  8  18  18  8  18  18  72
1 3  2
El determinante da distinto de 0 → Rg M = 3
Rg M = 3 = Rg M* = nº de incógnitas SCD

9.  Rango de M*
1 3 11
3 4 1 
1 3 1
 1 3 2 11 
 
M *   3 4  6  1 1 2 11
1 3  2 1  3  6 1 
 
1  2 1
3 2 11
1 3 2
4  6 1 
3 4  6  8  18  18  8  18  18  72
3 2 1
1 3  2
El determinante da distinto de 0 → Rg M* = 3

10.  El valor de las incógnitas se obtiene como
cociente de determinantes.
Como denominador se coloca el determinante
de la matriz de los coeficientes o del sistema.
¿ ...? ¿ ...?
¿ ...?
x   y   z  
1 3 2 1 3 2 1 3 2
3 4 6 3 4 6 3 4 6
1 3 2 1 3 2 1 3 2

11.  Como numerador se pone el mismo
determinante cambiando la primera columna si
se trata de la x, la segunda columna si se trata
de la y, la tercera columna si se trata de la z, y
así sucesivamente.
¿ ...? 3 2
¿ ...? 4 6 1 3 ¿ ...?
¿ ...? 3 2 3 4 ¿ ...?
x    1 3 ¿ ...?
1 3 2 z  
1 ¿ ...? 2 1 3 2
3 4 6
3 ¿ ...? 6 3 4 6
1 3 2
 1 ¿ ...? 2 1 3 2
y  
1 3 2
3 4 6
1 3 2

12.  En su lugar se ponen los términos
independientes
11 3 2
1 4 6
1 3 2  88  6  18  8  6  198 72
x    1
1 3 2  8  18  18  8  18  18 72
3 4 6
1 3 2
1 11 2
3 1  6
1 1 2 2  6  66  2  6  66 144
y     2
1 3 2  8  18  18  8  18  18 72
3 4 6
1 3 2
1 3 11
3 4 1
1 3 1 4  99  3  44  3  9 144
z     2
1 3 2  8  18  18  8  18  18 72
3 4 6
1 3 2
Sol : ( x , y , z ) Sol : (1,2,2)

13. MÉTODO DE GAUSS
 Se puede aplicar siempre en cualquier
sistema, y es el más aconsejable para
sistemas compatibles indeterminados (SCI)
con ∞ soluciones
Rg M = Rg M* < nº de incógnitas
x  2 y  2z  1  1  2 2  1  2 2 1 
   
 M   3 1  4 M*   3 1  4  1
3 x  y  4 z  1 
 2 3  6  2 3  6  2
2 x  3 y  6 z  2
    

14.  Rango de M
1  2 2 
 
M   3 1  4
 2 3  6
 
1 2 2
3 1  4  6  18  16  4  12  36  46  46  0
2 3 6
El determinante da 0 → Rg M = 2

15.  Rango de M*
1 2 1
3 1  1  2  9  4  2  3  12  0
2 3 2
1  2 2 1  1 2 1
 
M*   3 1  4  1
3  4  1  8  18  4  8  6  12  0
 2 3  6  2
  2 6 2
2 2 1
1  4  1  16  6  6  12  12  4  0
1 2 2 3 6 2
3 1  4  6  18  16  4  12  36  0
2 3 6
Todos los determinante dan 0 → Rg M* = 2
Rg M = 2 = Rg M* < nº de incógnitas (SCI)

16.  Se trabajará con tantas ecuaciones como indique
el rango del sistema. Cogeremos siempre las
ecuaciones más sencillas.
x  2 y  2z  1 
 x  2 y  2z  1 
3 x  y  4 z  1  Rg M = 2 = Rg M* 
2 x  3 y  6 z  2
 3 x  y  4z  1
 Tenemos más incógnitas que ecuaciones.
 A partir de ahora vamos a considerar que tenemos
tantas ecuaciones como incógnitas. Pasamos las
incógnitas que nos sobra a la otra parte de la
igualdad y pasarán a considerarse parámetros.

17. x  2 y  2z  1  x  2 y  1  2z 
 
3 x  y  4z  1 3 x  y  1  4z 
 Por reducción o Gauss hallamos las
incógnitas, que generalmente dependerán de
los parámetros o incógnitas que hemos pasado
x  2 y  1  2z  E1 = E1 x  2 y  1  2z 
 
3 x  y  1  4z  E2 = - 3E1 + E2 7 y  4  10z 
 4  10z
y x  2 y  1  2z
7
  4  10z    4  10z  7  14z  8  20z  1  6z
x  2   1  2z x  1  2z  2    
 7   7  7 7
  1  6 z  4  10z 
Sol :  , , z)
Sol : ( x , y , z )  7 7 

18. ¡¡¡NOS CALLAMOS!!!

19. Me parece
que hay
demasiada
gente
hablando

20. ¡A quien
no le
interese
que se
vaya al
patio a
jugar al
fútbol!

21. Si atendemos un poco,
no es tan difícil

22. No le des tanto al pico

23. ¡¡¡Cierra la boca de una vez!!!

24. ¿Se entiende lo que explico?

25. Esto se
acabó, o
como decía
un colega:
“SAYONARA
BABY”