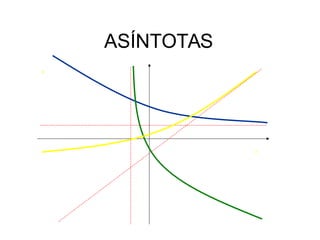
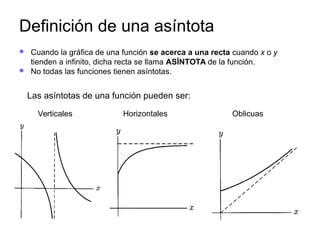
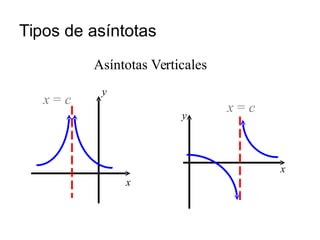
Este documento describe los diferentes tipos de asíntotas de funciones: verticales, horizontales y oblicuas. Explica que una asíntota es una recta a la que se acerca el gráfico de una función cuando el dominio tiende a cierto valor. Proporciona ejemplos detallados de cómo calcular cada tipo de asíntota para funciones racionales.

1. ASÍNTOTAS

2. Definición de una asíntota
 Cuando la gráfica de una función se acerca a una recta cuando x o y
tienden a infinito, dicha recta se llama ASÍNTOTA de la función.
 No todas las funciones tienen asíntotas.
Las asíntotas de una función pueden ser:
Verticales Horizontales Oblicuas

3. Tipos de asíntotas
x = c
y
x
Asíntotas Verticales
x = c
y
x

4. Tipos de asíntotas
y = L
y = f(x)
y
x
y = L
y = f(x)
y
x
Asíntotas Horizontales

5. Tipos de asíntotas
Asíntotas Oblicuas
y
x
y = ax + b

6. Asíntotas verticales
f (x)=+∞ f (x)=−∞
f (x)=+∞
La recta x = c es una asíntota vertical de una función f(x) si se cumple alguna
de las siguientes condiciones:
f (x)=+∞
Ejemplo:
1
x−2
=−∞
1
x−2
=+ ∞
f (x)=
1
x−2
La recta x = 2 es una asíntota vertical

7. Asíntotas horizontales
f ( x)=L f ( x)=L
La recta x = L es una asíntota horizontal de una función f(x) si se cumple
alguna de las siguientes condiciones:
Ejemplo:
f (x)=
2 x
x−1
2 x
x −1
=2
2 x
x −1
=2
La recta y = 2 es una asíntota horizontal

8. Asíntotas oblicuas
f ( x )
x
=a
f ( x )
x
=a
(f (x)−ax)=b
La recta y = ax + b es una asíntota oblicua de una función f(x) si se
cumple alguna de las siguientes condiciones:
a)
b)
(f (x)−ax)=b
Ejemplo:
f (x)=
2 x
2
x−1
2 x
2
x 2
− x
= 2
(
2 x
2
x −1
−2 x )=2
La recta y = 2x+2 es una asíntota oblicua

9. Asíntotas de funciones racionales
Una función racional tiene una asíntota vertical cuando el denominador de la
función simplificada es igual a 0.
Recuerda que se simplifica cancelando los factores comunes del numerador y
denominador.
Asíntotas Verticales

10. Ejemplo 1: Calcular las asíntotas verticales
f (x)=
2−5 x
2+2 x
Dada la función
Calculamos los valores de x
que hacen 0 el denominador:
2 + 2x = 0  x = -1
La recta x = -1 es la única
asíntota vertical de la
función.
Asíntota vertical
x = -1

11. Primero simplicamos la función.
f (x)=
2x
2
+10 x+12
x2
−9
2 x2
+10 x+12
x3
−9
=
(x+3)(2 x+4)
(x+3)(x−3)
2 x+4
x−3
La(s) asíntota(s) aparecen cuando el
denominator (después de simplificar)
es igual a 0.
x – 3 = 0  x = 3
La recta vertical x = 3 es la única
asíntota vertical de esta función.
Ejemplo 2: Calcular las asíntotas verticales

12. g(x)=
x−5
x2
−x−6
x−5
x2
−x−6
=
x−5
(x+2)(x−3)
El denominador es igual a 0 cuando
x + 2 = 0  x = -2
o
x - 3 = 0  x = 3
Esta función tiene dos asíntotas
verticales, una x = -2 y la otra x = 3
Ejemplo 3: Calcular las asíntotas verticales

13. Asíntotas horizontales
Las asíntotas horizontales aparecen cuando ocurre una de las siguientes
condiciones (ambas condiciones no pueden ocurrir en la misma función):
 El grado del numerador es menor que el grado del denominador. En
este caso, la asíntota es la recta horizontal y = 0.
 El grado del numerador es igual al grado del denominador. En este
caso, la asíntota es la recta horizontal y = a/b, donde a es el coeficiente
de mayor grado del numerador y b es el del denominador.
Cuando el grado del numerador es mayor que el grado del denominador la
función no tiene asíntota horizontal.

14. Ejemplo 4: Calcular las asíntotas horizontales
x
2
+3 x −5
x3
−27
=0
f (x)=
x
2
+3 x−5
x3
−27
x
2
+3 x−5
x3
−27
=0
Tiene una asíntota horizontal en
la recta y = 0 porque el grado del
numerador (2) es menor que el
grado del denominador (3).
La recta horizontal y = 0 es
la asíntota horizontal.

15. Ejemplo 5: Calcular las asíntotas horizontales
6 x
2
−3 x+5
5 x2
+7 x−9
=
6
5
g(x)=
6 x
2
−3 x+5
5 x2
+7 x−9
El grado del numerador (2) es
igual al grado del denominador
(2), luego la recta y = 6/5 es una
asíntota horizontal.
La recta y = 6
/5 es la
asíntota horizontal.

16. Ejemplo 6: Calcular las asíntotas horizontales
f (x)=
−2 x
3
+5 x−9
x2
+1
No tiene asíntotas
horizontales porque el
grado del numerador es
mayor que el grado del
denominador.

17. Asíntotas oblicuas
Las asíntotas oblicuas aparecen cuando
el grado del numerador es exactamente
una unidad mayor que el grado del
denominador.

18. Ejemplo 7: Calcular las asíntotas oblicuas
f (x)=
x
3
+2 x
2
+5 x−9
x2
−x+1
Tiene una asíntota oblicua
porque el grado del numerador
(3) es uno más que el grado del
denominador (2).
x
3
+2 x
2
+5 x −9
x3
−x2
+x
=1
3 x
2
+ 4 x− 9
x2
− x+1
=3
La recta y = x + 3 es
asíntota oblicua

19. Problemas
Calcula las asíntotas verticales, horizontales y oblicuas
de las funciones:
 
2
2
2 15
7 10
x x
f x
x x
 

 
Vertical: x = -2
Horizontal : y = 1
Oblicua: no tiene
 
2
2 5 7
3
x x
g x
x
 


Vertical: x = 3
Horizontal : no tiene
Oblicua: y = 2x +11

20. 20
Ejemplo
Determine las asíntotas verticales y horizontales
de las gráficas de las funciones:
2
( )
2
x
f x
x



2
4
( )
2
x
f x
x



1.
2.
3.
2
2
4
( )
2
x
f x
x x




21. 4. Hallar las asíntotas horizontales y las
asíntotas verticales de la gráfica de la
función:
f ( x)=
2x
2
+3
3 x2
−2 Rpta: A.H. y =2/3
A.V . x =±
√2
3

22. Determinar la asíntota oblicua
de :
f ( x)=
x
3
x2
+1
Rpta: y = x

23. Determinar las ecuaciones de las asíntotas de
las siguientes funciones:
1. 3.
2.
f (x)=
x
2
−1
x
f (x)=
2 x+1
x+2
f (x)=
3 x−10
x−3
Rpta: 1) A.V. x = 0
A.O. y = x
2) A.H. y = 2
A.V. x =–2
3) A.H. y = 3
A.V. x = 3

24. Ejercicio:
Trace la gráfica de una función f que cumpla con las siguientes
condiciones:
a) dom(f) = R – {-2}
b) y
c) , f(0) = 3
d) , y f(3) = 1
f ( x)=1 f (x)=−1
f (x)=1
f (x)=2 f (x)=1

25. Continuidad

26. Continuidad

27. Ejemplo

28. Ejemplo

29. Ejemplo

30. Ejemplo

31. Tipos de discontinuidad

32. f ( x)=√4−x2
y
x
-2 2
2
Analizar la continuidad de la función f en su
extremo izquierdo y extremo derecho de su
dominio
Ejemplo 1

33. La función f es continua en el intervalo
abierto ]a;b[ si es continua en todos sus
puntos.
y
x
-2 2
2
Continuidad en un intervalo abierto

34. La función f es continua en el intervalo cerrado
[a;b] si es continua en el intervalo abierto ]
a;b[ y es continua a la derecha de “a” y a la
izquierda de “b”.
y
x
-2 2
2
Continuidad en un intervalo cerrado

35. Ejemplo
En una playa de estacionamiento, se cobran 3
dólares por la primera hora o fracción y 2
dólares por cada hora o fracción subsiguiente,
hasta un máximo diario de 10 dólares.
a. Grafique la función costo de estacionar un automóvil
C(t) como función del tiempo que permanezca allí
durante un día.
b. Indique si la función C(t) es contínua o no, de no ser
indique los valores en donde es discontínua.

36. Operaciones y Composición de
Funciones Continuas

37. Ejemplos

38. Ejemplos

39. Ejemplos

40. Ejemplos

41. Ejemplos
X

42. Algunos teoremas