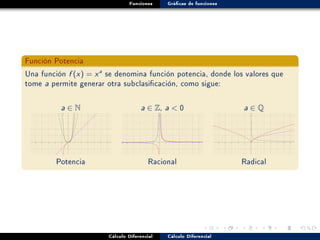
Este documento define funciones y tipos de funciones. Explica que una función asigna un único valor de salida a cada valor de entrada. Luego describe funciones lineales, polinómicas, trigonométricas, exponenciales y logarítmicas. Finalmente, clasifica funciones como pares e impares dependiendo de su simetría.

1. Funciones
Cálculo Diferencial Cálculo Diferencial

2. Funciones
Cálculo Diferencial
Adriana Quintero Palomino
Departamento de Matemáticas, Física y Estadística
Universidad de La Sabana
3 de abril de 2018
Cálculo Diferencial Cálculo Diferencial

3. Funciones Grácas de funciones
Denición: Función;
Una función f de un conjunto D a un conjunto Y es una regla que asigna un
elemento único f (x) ∈ Y para cada elemento x ∈ D.
El conjunto D de los valores de entrada posible se llama Dominio. El conjunto
de todos los valores f (x), a medida que x varia en D, se denomina Rango de la
función.
Ejemplo: Algunas Funciones, sus doominios y rangos.
Función Dominio (x) Rango (y)
f (x) = x3
(−∞, ∞) (−∞, ∞)
f (x) = 1
x
(−∞, 0) ∪ (0, ∞) (−∞, 0) ∪ (0, ∞)
f (x) =
√
2 − x (−∞, 2] [0, ∞)
f (x) = ln(x) (0, ∞) (−∞, ∞)
Cálculo Diferencial Cálculo Diferencial

4. Funciones Grácas de funciones
Algunas Grácas
A continuación se muestran las grácas de las funciones anteriores, para que se
realice la vericación visual de los valores enunciados:
Función Gráca Función Gráca
f (x) = x3
f (x) = 1
x
f (x) =
√
2 − x f (x) = ln(x)
Cálculo Diferencial Cálculo Diferencial

5. Funciones Grácas de funciones
Prueba de la recta vertical para una función
La totalidad de las curvas que se gráca en el plano de coordenadas, no pueden
ser denominadas funciones, por lo anterior existe la pruebba de la línea vertical,
para la cual se observa que si al trazar innitas líneas verticales, existe al menos
una la cual corte a la curva en dos o mas puntos, dicho gráco no representa
una función.
Función No función
Cálculo Diferencial Cálculo Diferencial

6. Funciones Grácas de funciones
Funciones denidas a trozos
Un función denida a trozos es aquella que presenta distintas fórmulas a lo
largo de su dominio.
f (x) =



f1(x) si x a,
f2(x) si x ≥ a,
Ejemplo: Función a trozos
Función
f (x) =



sen(x) si x −2,
√
2 − x si −2 ≤ x ≤ 0,
Ln(x) si x 0,
Gráca
Cálculo Diferencial Cálculo Diferencial

7. Funciones Grácas de funciones
Simetría: Funciones pares e impares
Un función y = f (x) se denomina
función par de x si f(-x)=f(x)
función impar de x si f(-x)=-f(x)
para toda x en el dominio de la función.
La gráca de una función par es simétrica respecto al eje y y la de una función
impar es simétrica al origen.
Ejemplo: Función a trozos
Función Par Función Impar
f (x) = x2−1
x2−4
f (x) = x
x2−2
Cálculo Diferencial Cálculo Diferencial

8. Funciones Grácas de funciones
Clasicación de Funciones
Existen varios tipos de funciones, entre las más comunes se pueden resaltar:
Función Lineal
Un función f (x) = mx + b, donde m y b son constantes, se denomina función
lineal.
m = 0, b = 0 m = 0, b = 0
Cálculo Diferencial Cálculo Diferencial

9. Funciones Grácas de funciones
Función Potencia
Una función f (x) = xa
se denomina función potencia, donde los valores que
tome a permite generar otra subclasicación, como sigue:
a ∈ N a ∈ Z, a 0 a ∈ Q
Potencia Racional Radical
Cálculo Diferencial Cálculo Diferencial

10. Funciones Grácas de funciones
Función Polinómica
Una función f (x) se denomina función polinómica si
f (x) = anxn
+ an − 1xn−1
+ . . . + a1x + a0
f (x) = 5x4
+ 2x + 3 f (x) = x5
− 2x3
+ x + 2
Cálculo Diferencial Cálculo Diferencial

11. Funciones Grácas de funciones
Función Algebraica
Una función f (x) se denomina función algebraica si está conformado por
operaciones básicas entre funciones polinómicas.
f (x) = x1/3
(x + 3) f (x) = x(1 − x2
)2/3
Cálculo Diferencial Cálculo Diferencial

12. Funciones Grácas de funciones
Función Trigonométrica
Dos de las funciones trigonométricas básicas se muestran a continuación:
f (x) = sen(x) f (x) = cos(x)
Cálculo Diferencial Cálculo Diferencial

13. Funciones Grácas de funciones
Función Exponencial
Una función f (x) se denomina exponencial si f (x) = ax
, con a 0.
f (x) = ax
f (x) = a−x
Función Logarítmica
Una función f (x) se denomina logarítmica si f (x) = loga(x), con a constante
positiva y a = 1.
Cálculo Diferencial Cálculo Diferencial