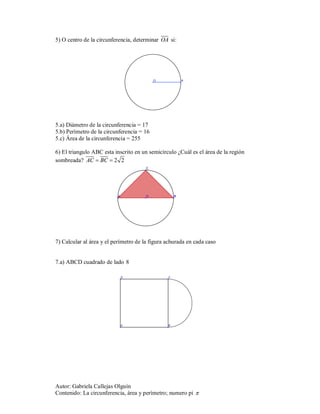
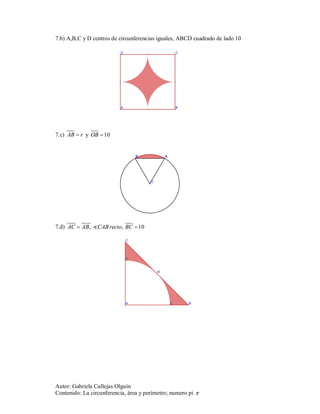
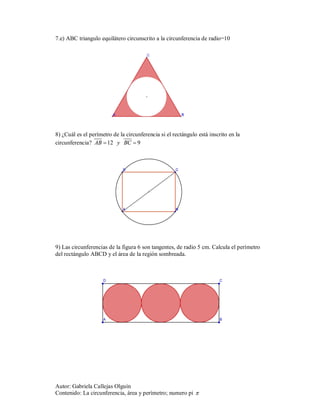
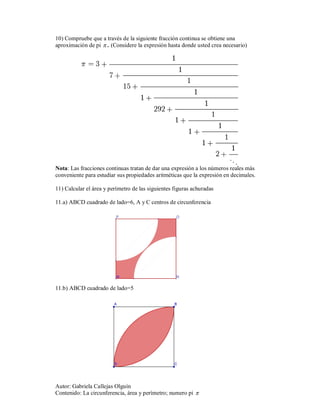
Este documento presenta una guía de ejercicios sobre el cálculo del área y perímetro de circunferencias utilizando el número pi. Incluye 14 ejercicios que abarcan temas como calcular el perímetro y área de circunferencias dadas su radio, calcular distancias recorridas por ruedas girando, y calcular áreas y perímetros de figuras compuestas de cuadrados, triángulos y semicírculos.