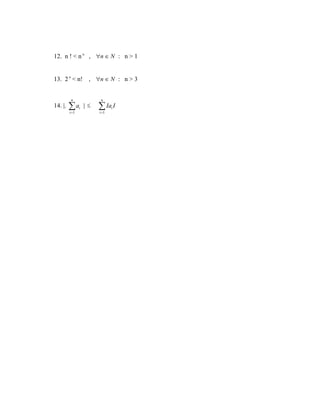Este documento presenta una serie de ejercicios de inducción matemática para sumas, desigualdades, divisibilidad y el binomio de Newton. Los ejercicios piden demostrar diferentes fórmulas y propiedades matemáticas utilizando inducción matemática. Adicionalmente, se pide conjeturar fórmulas para diferentes sumas.

1. TAREA # 1
INDUCCIÓN MATEMÁTICA.
En los siguientes ejercicios, para sumas, demuestre lo afirmado por inducción matemática.
1. 
=
n
i
i
1
=
2
)
1
( +
n
n
2. 
=
n
i
i
i
1
!
* = (n+1)! –1
3. 
=
−
n
i
i
1
3
)
1
2
( = 2
n (2n 2
-1)
4. 
=
n
i
i
1
2
=
6
)
1
2
)(
1
( +
+ n
n
n
5. 
=
n
i
i
1
3
= (
2
)
1
( +
n
n
) 2
6. 
=
−
n
i
i
1
)
2
6
( = n(3n+1)
7. 
=
n
i
i
1 2
1
= 1- n
2
1
8. 
= +
−
n
i i
i
1 )
2
3
)(
1
3
(
1
=
4
6 +
n
n
9. 
=
n
i
i
i
1
3 =
4
3
)
1
2
( )
1
( +
− n
n
+
4
3
10. 
=
+
n
i
id
a
0
)
( =
2
)
2
)(
1
( nd
a
n +
+
11. 
= +
+
n
i i
i
i
1 )
2
)(
1
(
1
=
)
2
)(
1
(
4
)
3
(
+
+
+
n
n
n
n

2. 12. ( a + b ) n
= 
=








n
i i
n
0
a i
n−
bi
, N
n 
 ; a 0
 y b 0
 .
13. )
(
1
i
n
i
i b
a +

=
=
=
n
i
i
a
1
+ 
=
n
i
i
b
1
14. 
=
n
i
i
ca
1
= c 
=
n
i
i
a
1
, c R

15. 
=
n
i
i
a
1
= 
−
=
+
1
0
1
n
i
i
a
16. 
=
n
i
i
a
0
= 
+
=
−
1
1
1
n
i
i
a
17. 
=
−
n
i
i
ar
10
1
= a 







−
−
r
rn
1
1
; si a R
 y r R
 - 0,1 
18. 
=
−
n
i
x
i
sen
1
)
1
2
( =
senx
nx
2
)
2
cos(
1−

3. TAREA # 2
INDUCCIÓN MATEMÁTICA.
En los siguientes ejercicios, para desigualdades, demuestre lo afirmado por inducción
matemática.
1. 2n+1 < 2 n
, N
n 
 : n 3

2. 2 n
> n 2
, N
n 
 : n 5

3. n < 2 n
, N
n 

4. si a > 1  a n
> 1 , N
n 

5. 3 n
 1+ 2 n
, N
n 

6. n 4
< 4 n
, N
n 
 : n 5

7. N
n 
 : n > 2  





+
n
1
1 n
2

8. N
n 
 : n >1 
n
n
n





 +1
> n 
9. (1 + x ) n
> 1 + nx , si n > 1 ; xR , x -1
10. 2 1
−
n
(a n
+ b n
) > (a + b) n
, siempre que a+b  0 ; a  b y n > 1
11. 3 n
< n  , N
n 
 : n > 6

4. 12. n  < n n
, N
n 
 : n > 1
13. 2 n
< n , N
n 
 : n > 3
14. . 
=
n
i
i
a
1
  I
Ia
n
i
i

=1

5. TAREA # 3
INDUCCIÓN MATEMÁTICA.
En los siguientes ejercicios, para divisibilidad, demuestre lo afirmado por inducción
matemática.
1. N
n 
 , 64  3 2
2 +
n
- 8 n - 9
2. N
n 
 , 9  4 n
- 3 n – 1
3. N
n 
 , 5  7 n
- 2 n
4. N
n 
 , 3  4 n
- 1
5. N
n 
 , 24  5 n
2
- 1
6. N
n 
 , 3  n3
- 4 n + 6
7. N
n 
 , 8  5 1
+
n
+ 2 * 3 n
+ 1
8. N
n 
 , 7  11 n
- 4 n
9. N
n 
 , 7  3 1
2 +
n
+ 2 2
+
n
10. N
n 
 , ( x – y )  x n
- y n

6. TAREA # 4
INDUCCIÓN MATEMÁTICA.
En los siguientes ejercicios, para el binomio de Newton, demuestre lo afirmado por
inducción matemática.
1. ( a + b ) n
= 
=








n
i i
n
0
a i
n−
bi
, N
n 
 ; a 0
 y b 0
 .
2. n
n
i i
n
2
0
=









=
3. ( ) 0
1
0
=
−









=
i
n
i i
n
4. Demostrar que en el desarrollo de ( a + b ) n
, la suma de los coeficientes de las
potencias pares de a es igual a la suma de los coeficientes de las potencias de
impares de b.
5. N
n 
 : n > 2  





+
n
1
1 n
2

6. N
n 
 : n >1 
n
n
n





 +1
> n 
7. (1 + x ) n
> 1 + nx , si n > 1 ; xR , x -1
8. 2 1
−
n
(a n
+ b n
) > (a + b) n
, siempre que a+b  0 ; a  b y n > 1

7. TAREA # 5
INDUCCIÓN MATEMÁTICA.
En los siguientes ejercicios, miscelánea , demuestra lo afirmado por inducción
matemática.
1. x n
2
> 0 , si x  0 y N
n 

2. Un polígono de n lados tiene n vértices, N
n 
 : n > 2
3. ( a n
) m
= a nm
, N
m
n 
 , y aR
4. La suma de los ángulos interiores de un polígono de n lados es ( n – 2 ) 180 °
N
n 
 : n > 2
5. N
k
m









; N
m
k 
 , ; k  m .
6. Todo entero positivo mayor que uno se puede escribir como producto de números
primos.
7. Sean a i ( i = 1, 2 , ... , n ) números reales, tales que  a 1
  1 y  a n - a 1
−
n   1
entonces  a n   n .
8. La suma de los cubos de tres enteros positivos consecutivos, cualesquiera, es
divisible por tres.
9. N
n 
 ,
3
)
2
3
( 2
3
n
n
n +
+
es un número entero.

8. 10. N
n 
 ,
6
)
3
2
( 2
3
n
n
n +
+
es un número entero.
12.  (1+a
k
2
) =
a
a n
−
− +
1
1 1
2
, k= 0,1, ... , n
En los siguientes ejercicios, conjeture una fórmula para cada una de las sumas que se
indican.
1. 
=
−
n
i
i
1
3
)
1
2
( =
2. 
=
n
i
i
1
3
)
2
( =
3. 
=
+
n
i
i
i
1
)
1
( =
4. 
=
n
i
i
1
2 =
5. 
=
+
n
i
i
1
)
1
2
( =
6. 
=
−
n
i
i
1
)
2
3
( =
7. 
=
−
n
i
i
1
)
3
4
( =
8. 
= +
−
n
i i
i
1 )
1
2
)(
1
2
(
1
=