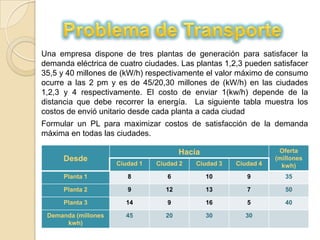
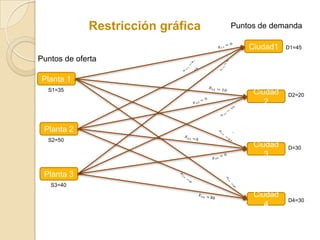
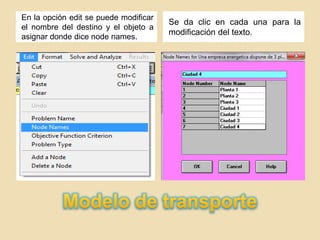
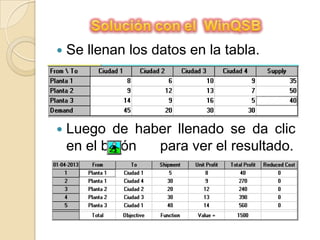
El documento describe un problema de optimización para maximizar la satisfacción de la demanda eléctrica de cuatro ciudades a partir de tres plantas de generación. Cada planta tiene una capacidad máxima de producción en millones de kW/h. El costo de enviar la electricidad depende de la distancia entre cada planta y ciudad. Se debe formular un programa lineal para maximizar la satisfacción de la demanda máxima en todas las ciudades utilizando la energía de las tres plantas de manera óptima.

2. Una empresa dispone de tres plantas de generación para satisfacer la
demanda eléctrica de cuatro ciudades. Las plantas 1,2,3 pueden satisfacer
35,5 y 40 millones de (kW/h) respectivamente el valor máximo de consumo
ocurre a las 2 pm y es de 45/20,30 millones de (kW/h) en las ciudades
1,2,3 y 4 respectivamente. El costo de enviar 1(kw/h) depende de la
distancia que debe recorrer la energía. La siguiente tabla muestra los
costos de envió unitario desde cada planta a cada ciudad
Formular un PL para maximizar costos de satisfacción de la demanda
máxima en todas las ciudades.
Hacia Oferta
Desde (millones
Ciudad 1 Ciudad 2 Ciudad 3 Ciudad 4 kwh)
Planta 1 8 6 10 9 35
Planta 2 9 12 13 7 50
Planta 3 14 9 16 5 40
Demanda (millones 45 20 30 30
kwh)

4. 

5. Restricción gráfica Puntos de demanda
Ciudad1 D1=45
Puntos de oferta
Planta 1
S1=35
Ciudad D2=20
2
Planta 2
S2=50
Ciudad D=30
3
Planta 3
S3=40
Ciudad
D4=30
4

6. Se elige el tipo de
problema en este
caso es el de
modelo de
transporte, como
el ejercicio
requiere que
maximice costos
entonces en el
objetivo se marca
maximization.

7. En la opción edit se puede modificar
Se da clic en cada una para la
el nombre del destino y el objeto a
modificación del texto.
asignar donde dice node names.

8.  Se llenan los datos en la tabla.
 Luego de haber llenado se da clic
en el botón para ver el resultado.

9.  Al barco 1 se le debe asignar al puerto 1
con un costo de $500.
 Al barco 2 se le debe asignar al puerto 4
con un costo de $500.
 Al barco 3 se le debe asignar al puerto 2
con un costo de $500.
 Al barco 4 se le debe asignar al puerto 3
con un costo de $600.
 El costo mínimo total es de 2100 para
todos los barcos.