Descargado 79 veces
Subido porDavid Choquejahua
Recursosdidacticosmate
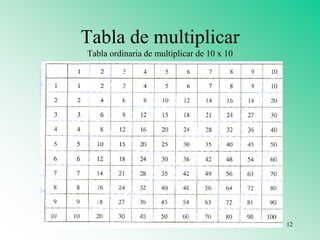
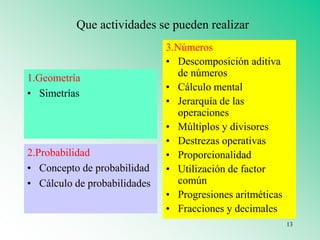
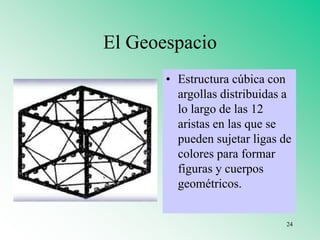
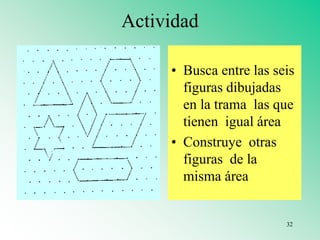
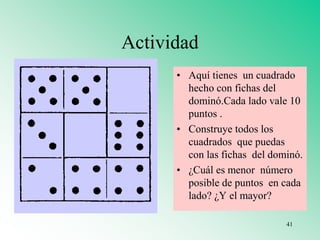
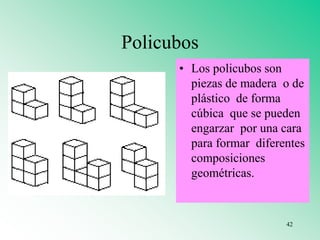
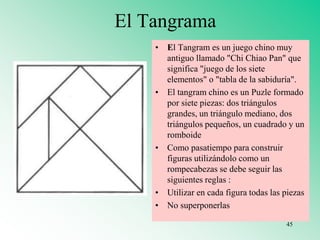
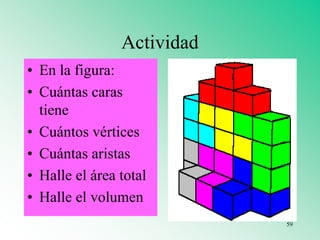
El documento presenta varios materiales didácticos para la enseñanza de las matemáticas, como palillos, el ábaco, tablas de multiplicar, geoplanos, regletas Cuisenaire, dominós y policubos. Describe las actividades que se pueden realizar con cada material para cubrir temas de números, geometría, medida y probabilidad de manera lúdica y práctica.
Más contenido relacionado
La actualidad más candente
Similar a Recursosdidacticosmate
Recursosdidacticosmate
- 1.
- 2. ¿Qué son losmateriales didácticos? Por materiales didácticos se entiende todos aquellos objetos, juegos , medios técnicos etc. capaces de ayudar al alumno a suscitar preguntas , sugerir conceptos o materializar ideas abstractas . 2
- 3. Objetivos • Potenciar unaenseñanza mas rica, mas activa, mas creativa y mas participativa de los temas habituales del currículo de matemáticas en primaria y secundaria • Cambiar las actitudes de los alumnos hacia las matemáticas , haciéndolas mas positivas . • Romper paradigmas pedagógicos en la enseñanza –aprendizaje de las matemáticas • Propiciar espacios lúdicos que permitan aprender las matemáticas desde actividades de juego 3
- 4. Ventajas del trabajocon materiales didácticos • Proporciona una fuente de actividades matemáticas estimulantes • Permite que los alumnos realicen actividades de forma autónoma • Se puede adaptar al trabajo en grupo sobre un tema en particular • Sugiere ideas y puntos de partida para diseñar una clase • Se puede adaptar a cualquier programación didáctica 4
- 5.
- 6. Palillos Palillos de madera ode plástico largos y cortos y de diferentes colores . La longitud de los palillos largos debe ser el doble de la de los cortos . 6
- 7. Que actividades sepueden realizar 1.Geometría • Intersección de rectas • Areas y perímetros • Lugares geométricos • Simetrías • Construcción y clasificación de polígonos • Angulos en un polígono • Clasificación de triángulos • Angulos • Perpendicularidad y paralelismo • Rectas y segmentos • Polígonos 2.Números • Progresiones aritméticas • Números triángulares • Múltiplos y divisores • Técnicas de recuento 3.Medida • Areas y perímetros • Medidas de lados y ángulos 7
- 8. Actividad • Construye cuadriláteroscon cuatro palillos y clasifiquelos • Construye pentágonos con cinco palillos. ¿son equiláteros? ¿Son regulares? • Clasificalos según el número de ángulos rectos y según los ejes de simetría • Cuáles son iscriptibles y cuáles circunscriptibles. 8
- 9. El Abaco El ábacoes una calculadora que proviene de la antigua China. Consiste en hileras de unidades, las decenas, las centenas y los millares. En muchos pueblos asiáticos se usa todavía para sumar, restar, multiplicar y dividir con rapidez. En las figuras se observa un ábaco vertical y un ábaco horizontal 9
- 10. Que actividades sepueden realizar • Contar • Sumar • Restar • Multiplicar • Dividir 10
- 11. Actividad • ¿Cómo representasel número 539? • ¿Cómo representas el número 1024? • ¿Cómo representas el número 43? 11
- 12. Tabla de multiplicar Tablaordinaria de multiplicar de 10 x 10 12
- 13. Que actividades sepueden realizar 1.Geometría • Simetrías 2.Probabilidad • Concepto de probabilidad • Cálculo de probabilidades 3.Números • Descomposición aditiva de números • Cálculo mental • Jerarquía de las operaciones • Múltiplos y divisores • Destrezas operativas • Proporcionalidad • Utilización de factor común • Progresiones aritméticas • Fracciones y decimales 13
- 14. Actividad • Colorea losnúmeros de la tabla que terminan en cuatro . Une mediante segmentos las celdas coloreadas . Estudia la simetría de la figura formada. • En una tabla de multiplicar vacía excepto la fila superior y la columna de la izquierda, colorea los números que terminan en 3, en 5, en 6 ....... Estudia los modelos • Construye la tabla de multiplicar escribiendo solo las unidades de cada producto . Busca simetrías . 14
- 15. El Geoplano Cuadrado •Panel en forma de cuadrado con clavos distribuidos formando una trama cuadrada de 5 x 5 o también de 11 x 11 en la que se pueden sujetar elásticos para formar figuras geométricas. 15
- 16. Que actividades sepueden realizar 1.Números • Estrategias de recuento • Números irracionales • Diagramas de árbol • Idea intuitiva de límite 2.Medida • Cálculo de áreas y perímetros • Longitudes • Medida de ángulos • Caminos de longitud mínima 3. Geometría • Polígonos • Cuadriláteros • Medida de segmentos • Clasificación de triángulos • Congruencia y semejanza • Teorema de pitágoras • Angulos • Simetrías • Traslaciones, giros • Movimientos • Cuadrados 16
- 17. Actividad • Construye unrectángulo.¿ Cuál es el área? • ¿Puedes construir retángulos cuyos lados no sean paralelos a los bordes del geoplano? ¿Cuál es su área? • Construye otros paralelogramos diferentes que tengan la misma área . Dibujalos en una trama cuadrada • Construy paralelogramos semejantes. ¿Cómo son sus lados , su perímetro y su área? ¿Cómo son sus ángulos? 17
- 18. Geoplano Circular • Panelde forma cuadrada con clavos formando dos círculos concéntricos en los que se pueden sujetar elásticos para formar diferentes figuras y elementos geométricos 18
- 19. Que actividades sepueden realizar 1. Números • Múltiplos y divisores 2.Medida • Medida de ángulos 3.Geometría • Clasificación de triángulos • Elementos de un polígono • Elementos de una circunferencia • Polígonos regulares • Polígonos estrellados • Angulos de una circunferencia • Angulos interiorres 19
- 20. Actividad • Construya unacircunferencia. Traza una cuerda, un diámetro,un radio,un ángulo inscrito y un ángulo central. ¿ Qué relación hay entre la medida del ángulo inscrito y la del central? 20
- 21. Regletas de Cuisenaire •Las regletas Cuisenaire son una colección de regletas, de planta rectangular, de diferentes tamaños y colores, si bien a una igualdad de tamaños va asociada una igualdad de colores. La más pequeña tiene una longitud de un centímetro, y las restantes aumentan de centímetro en centímetro, hasta la que tiene una longitud de 10 centímetros 21
- 22. Que actividades sepueden realizar • Cálculo de áreas • Perímetros • Polígonos • Proporcionalidad • Cuadriláteros • Conteo 22
- 23. Actividad • Si ledamos el valor 1 a la regleta blanca, ¿qué valor le daremos a las demás piezas? • Si le damos el valor 1 a la regleta amarilla, ¿qué valor le daremos a las demás piezas? • Si le damos el valor 1 a la regleta azul, ¿qué valor le daremos a las demás piezas? • Si le damos el valor 1 a la regleta naranja, ¿qué valor le daremos a las demás piezas? 23
- 24. El Geoespacio • Estructuracúbica con argollas distribuidas a lo largo de las 12 aristas en las que se pueden sujetar ligas de colores para formar figuras y cuerpos geométricos. 24
- 25. Que Actividades sepueden realizar • Construcción de cuerpos sólidos • Angulos • Volúmenes • Areas • Plano cartesiano • Visión espacial • Perspectivas • Interpretación de modelos 25
- 26. Actividad • Dibuja uncubo desde tres perspectivas distintas (pueden apoyarse en el geoespacio) • Construye en el geoespacio un prisma triangular. • Dibuja el prisma triangular desde tres perspectivas distintas. • Construye en el geoespacio un prisma rectangular. 26
- 27. Trama Cuadrada • Unatrama cuadrada es una hoja de papel punteado con los puntos situados en los vértices de cuadrados de aproximadamente 1cm de lado. 27
- 28. Que actividades sepueden realizar 1.Números • Raíz cuadrada • Divisibilidad:MCD,mcm • Fraccionarios • Números mixtos • Sucesiones númericas 3.Geometría • Construcciones geometricas • Poligonos • Semejanza • Teselaciones • Simetrías • Coordenadas 2.Medida • Angulos • Areas y perímetros • Medida de segmentos • Escalas 4.Estadística • Tabulación de datos • Combinatoria • Proporcionalidad • Probabilidad 28
- 29. Actividad • ¿Cuántos triángulospuedes construir de base 6 cms y área 9 cms cuadrados ? ¿ Y cuántos paralelogramos? • Construye 3 triángulos cuyas áreas estén en la relación 1:2:3. ¿ De cuántas formas puedes hacerlo? • Dibuja triángulos de base 5 y diferentes áreas. Representa las áreas en función de las alturas. 29
- 30. Trama Triangular • Unatrama triángular es una hoja de papel punteado formando una trama de triángulos equiláteros de 1 cm de lado. 30
- 31. Que actividades sepueden realizar 1.Números • Números racionales • Números irracionales • Conteo • Tabulaciones 2.Medida • Errores en medidas • Areas y perímetros • Congruencia • Teorema de pick 3.Geometría • Cuadrados • Triángulos y hexágonos • Areas y perímetros • Figuras cogruentes • Hexadiamantes • Desarrollo de poliedros • Angulos en polígonos • Teselaciones • Los nueve puntos en un triángulo • Teorema de pitágoras • Semejanza • Simetrias • Clasificación de figuras 31
- 32. Actividad • Busca entrelas seis figuras dibujadas en la trama las que tienen igual área • Construye otras figuras de la misma área 32
- 33. Trama Circular • Unatrama circular es una hoja de papel punteado formando una trama de círculos con los puntos distribuidos a la misma distancia a lo largo de la circunferencia 33
- 34. Que actividades sepueden realizar 1.Números • Divisibilidad • Divisores de un número • MCD • mcm 2.Medida • Angulos • Areas • Perímetros 3.Geometría • Polígonos inscritos • Polígonos estrellados • Angulos en la circunferencia • Triángulos inscritos en la circunferencia • Elementos del círculo • Elementos de la circunferencia • Clasificación de los polígonos • Teorema de pitágoras 34
- 35. Actividad • Une lospuntos de la circunferencia de 1 en 1 , de 2 en 2 , de 3 en 3 ,...¿ Qué observas? • ¿En qué casos obtienes un polígono en la primera vuelta? • ¿En qué casos has de dar mas de una vuelta para volver al punto de partida? • ¿En qué casos obtienes polígonos estrellados? • ¿Cuáles son los divisores del número de puntos de la circunferencia ? • ¿Encuentras alguna relación con MCD y mcm de los números? 35
- 36. Fichas de Colores •Se necesitan fichas de diferentes colores. Pueden servir las Fichas rojas, azules, amarillas y verdes comúnmente utilizadas para el juego del parchís. 36
- 37. Que actividades sepueden realizar 1.Números: • Progresiones aritméticas, descomposición aditiva de números, conteo , divisibilidad, números primos y compuestos, división entera, números módulo n , seriaciones , término general, cuadrados perfectos, múltiplos y divisores, números cuadrados, MCD. 2. Medida: • cálculo de áreas, cálculo de perímetros. 3. Geometría: • Triángulos, semejanza, polígonos regulares, coordenadas cartesianas ,giros, simetrías 4.Probabilidad: • Combinatoria, diagramas de árbol, muestreo, concepto de frecuencia y probabilidad. 37
- 38. Actividad • Tengo unascuantas fichas . Las coloco todas , tangentes unas a otras , formando un triángulo equilátero . Luego las agrupo y forman un cuadrado . ¿ Cuántas fichas tengo? 38
- 39. El Dominó Ordinario •Domino de 28 fichas 39
- 40. Que actividades sepueden realizar 1.Números Fracciones equivalentes Operaciones con fracciones Represntación gráfica de fracciones Ordenación de fracciones Proporcionalidad 3.Probabilidad Concepto de probabilidad Probabilidad de sucesos Probabilidad de la unión de sucesos Probabilidad de suceso complementario 2. Geometría Teorema de Thales Pendiente de una recta 40
- 41. Actividad • Aquí tienesun cuadrado hecho con fichas del dominó.Cada lado vale 10 puntos . • Construye todos los cuadrados que puedas con las fichas del dominó. • ¿Cuál es menor número posible de puntos en cada lado? ¿Y el mayor? 41
- 42. Policubos • Los policubosson piezas de madera o de plástico de forma cúbica que se pueden engarzar por una cara para formar diferentes composiciones geométricas. 42
- 43. Que actividades sepueden realizar 1.Geometría • Construcción de cuerpos geométricos • Semejanzas • Elementos del cubo • Teselaciones • Perspectivas 2.Medida • Areas • Volumenes 3.Números • Números cuadrados • Valor posicional de las cifras • Múltiplos • Sucesiones • Progresiones aritméticas • Diagramas de árbol • Descomposición aditiva de números • Técnicas de conteo • Combinatoria • Suma de números cuadrados 43
- 44. Actividad • Construye todaslas figuras que puedas con cuatro cubos del mismo color. • ¿Cuál de ellas tiene menor superficie? ¿Cuál tiene la mayor superficie? • ¿Con qué figuras idénticas de las que has hecho puedes formar un cubo de ocho cubitos ? • ¿De cuántas formas puedes partir en dos mitades iguals y encajables un cubo de 27 cubitos? ¿y uno de 64 cubitos? 44
- 45. El Tangrama • ElTangram es un juego chino muy antiguo llamado "Chi Chiao Pan" que significa "juego de los siete elementos" o "tabla de la sabiduría". • El tangram chino es un Puzle formado por siete piezas: dos triángulos grandes, un triángulo mediano, dos triángulos pequeños, un cuadrado y un romboide • Como pasatiempo para construir figuras utilizándolo como un rompecabezas se debe seguir las siguientes reglas : • Utilizar en cada figura todas las piezas • No superponerlas 45
- 46. Que actividades sepueden realizar 1. Números • Fracciones • Valores máximos y mínimos • Números irracionales 2.Medida • Medida de lados, diagonales y ángulos • Area y perímetro • Unidades de medida 3.Geometría • Construcción de figuras geométricas • Clasificación de polígonos • Elementos de un polígono • Teorema de pitágoras • Semejanza • Congruencia • Simetrías 46
- 47. Actividad • Tomando comounidad el cuadrado grande, halla el área de las siete piezas. • Forma figuras que tengan de área 7/16 unidades cuadradas. • Tomando como unidad el lado del cuadrado pequeño, halla el perímetro de tas siete piezas. • Forma las figuras de perímetro máximo y mínimo. • Forma figuras con un perímetro dado. • Descubre la relación entre los lados de las piezas. • Forma cuadrados, paralelogramos, trapecios,... • Forma figuras de igual área. • Comprueba el teorema de Pitágoras 47
- 48. El Pentominós • Elpentominós es un puzzle rectángular de doce piezas con diferentes formas , construida cada una de ellas por la unión de cinco cuadraditos iguales . 48
- 49. Que actividades sepueden realizar 1.Geometría • Construcción de polígonos • Semejanzas • Construcciones a escala • Polígonos congruentes 2.Medida • Perímetros • Areas • Volúmenes 49
- 50. Actividad • Halla elárea de cada una de las piezas del pentominós. Elija la unidad adecuada • Ordene las piezas según su perímetro • Estudia las simetrías de cada una de las piezas 50
- 51. Libro de losEspejos • El libro de los espejos consiste en dos espejos rectangulares unidos de forma que se pueda conseguir una abertura hasta 180 grados 51
- 52. Que actividades sepueden realizar • Geometría • Angulos • Creación de polígonos regulares • Circunferencia y círculo • Paralelismo y perpendicularidad • División de un segmento en partes iguales • División de un ángulo en ángulos iguales • Simetrías • Relaciones entre ángulos,ejes de simetría y número de lados 52
- 53. Actividad • Coloca ellibro de espejos sobre un rombo. ¿Qué figuras obtienes? • Haz lo mismo con un pentágono regular 53
- 54. Papiroflexia • La papiroflexia cconsisteen obtener figuras de diversa complejidad empleando papel. En general el papel que se emplea es cuadrado, aunque También se pueden emplear para algunas figuras otras formas de papel. Tiene sus orígenes en Japón, donde es conocida por la palabra 'origami', que significa doblar papel. 54
- 55. Que actividades sepueden realizar 1.Geometría • Areas y perímetros • Escalas • Máximos y mínimos • Paralelas y perpendiculares • Bisectriz de un ángulo • Construcción de polígonos • Construcción de circunferencias • Angulos • Polígonos • Volúmenes • Semejanza 2.Números • Lenguaje algebraico • Cuadrados de sumas • Proporcionalidad • Raíces cuadradas • Número de oro 3.Información • Concepto de función • Función lineal • Función cuadrática • Hipérbola equilátera 55
- 56. Actividad • Construya unaperpendicular a una recta dibujada en el papel • ¿Qué ángulos puedes construir? • Construye un cuadrado , un exágono, un octógono • Construye la bisectriz de un ángulo recto • Construye la raíz cuadrada de 2 y la raíz cuadrada de 3 • Encuentra los puntos característicos de un triángulo • Construye ángulos de 30° y 60° 56
- 57. El Cubo Soma •El Cubo Soma lo inventóó Piet Hein, un poeta, soñador, matemático y genio Danés en 1936. No fue un puzzle demasiado popular hasta 1969 cuando Parker Bros lo empaqueto como 'La respuesta 3D al Tangram', pero tuvo la mala suerte de coincidir con otro cubo de 27 piezas que se hizo mucho más popular y absorbió durante bastante tiempo la atención de los puzzles de forma cúbica 57
- 58. Que actividades sepueden realizar • Coordenadas en tres dimensiones • Angulos • Areas • Volúmenes • Visión espacial • Perspectivas • Modelación • Simetrías 58
- 59. Actividad • En lafigura: • Cuántas caras tiene • Cuántos vértices • Cuántas aristas • Halle el área total • Halle el volumen 59
- 60. • Consiste enun tablero con tres varillas verticales, en las que insertan discos de tamaños escalonados. A mayor número de discos, la resolución es más larga. (Pueden utilizarse monedas de tamaños diferentes, y prescindir de las varillas). • Al comenzar, los discos están ensartados en una varilla, colocados en tamaño decreciente. • El objetivo del juego es colocar todos los discos sobre otra de las varillas. • Los discos han de trasladarse de uno en uno, de una varilla a otra. • Ningún disco puede posar sobre otro menor que él. • Para n discos hacen falta 2n - 1 • (2 a la n menos 1) movimientos 60
- 61. Que actividades sepueden realizar • Series • Combinatoria • Conteo • Habilidad mental • Areas • Perímetros • Proporcionalidad • Volúmenes 61
- 62. Actividad • Cuál esel mínimo de movimientos para pasar 3 discos • Cuál es el mínimo de movimientos para pasar 6 discos • Cuál es el mínimo de movimientos para pasar 20 discos 62
- 63. Otros Recursos Didácticos •Existen otros recursos didácticos de gran uso en la enseñanza de las matemáticas ,los cuales solamente serán enumerados . • Tales recursos son: 63
- 64.
- 65.
- 66.
- 67. Fracciones Cuadrado yCírculo 67
- 68.
- 69.
- 70.
- 71.
- 72.
- 73.
- 74.
- 75.
- 76. Dominó de Angulosy Grados 76
- 77.
- 78. 4 En RayaTridimensional 78
- 79.
- 80.
- 81.
- 82.
- 83.
- 84.
- 85. Dados de Sumasy Restas 85
- 86. Triminó de Sumasal 10 86
- 87.
- 88. Bibliografía • Alsina, C;Pérez, R y Ruiz, C. (1989). Simetría dinámica. Síntesis. • Alsina, C; Pérez, R y Ruiz, C. (1989). Simetría dinámica. Síntesis. • Alsina, C. y Fortuny, J.M. (1992). Miralandia. Un viaje geométrico al país de los espejos. Proyecto Sur ed. Granada. • Bermejo, A. (2002). El libro de los espejos. Aplicaciones didácticas. Suma 41. 83-92: • Brihuega, J. (Coord.) (1995). Guía de recursos didácticos. Matemáticas. Secundaria Obligatoria. MEC. Madrid. • Hernan F. Y Carrillo, E. (1988). Recursos en el aula de Matemática. Síntesis. Madrid • Blanco, l. y Márquez, L. (1987). En torno al teorema de Pict: Una experiencia de Enseñanza de la Geometría. Números nº 16. Sociedad Canaria de Profesores de Matemáticas. Tenerife. 41-53. • Bolt, B. (1984). Mathematical activities. Cambridge. • Bolt, B. (1987). Divertimentos matemáticos. Labor. 88
- 89. •Arrieta, J.; Alvarez,J.L. y González, A.E. (1997). El teorema de pitágoras a partir de la manipulación con geoplanos. Suma 25. FESPM. 71-86 •Cascallana, M.T. (1988). Iniciación a la Matemática. Materiales y recursos didácticos. Santillana, Aula XXI. Madrid •Domínguez, M. (1991), El uso del geoplano en el aula de matemáticas. •En Sigma. Revista de Matemáticas nº 9, 31-40 •Gutiérrez, y Fernández (1984). Actividades diseñadas para la utilización del geoplano en EGB. Actas de las III JAEM. 355-361. •Smith, L. R. (1990). Areas and perimeters of geoboard polygons. •Matematics Teacher. NCTM 392.398 •Mora, J.A. (1995). Los recursos didácticos en el aprendizaje de la geometría. UNO nº 3. 101-115. •Brihuega, J. (Coord.) (1995). Guía de recursos didácticos. Matemáticas. Secundaria Obligatoria. MEC. Madrid. 89
- 90. •Balbuena, L. yCoba, (1992). La matemática recreativa vista por los alumnos. Proyecto sur edic. •Bolt, B. (1984). Mathematical activities. Cambridge. •Bolt, B. (1987). Divertimentos matemáticos. Labor. •Bueno, A. (1994). Apilamientos. Épsilon nº 29. SAEM Thales. Sevilla. 5- 60 •Guzmán, M. (1991). Para pensar mejor. Labor. Madrid. •Mark, F. (1998). Creaciones y trucos con palillos o cerillas y otros juegos de mesa. Altosa •Perelman, Y. (1982). Matemáticas recreativas 1. ED. Martínez Roca •Pérez, L. (1991). Un rato con los palillos. El material como hilo conductor. Épsilon 19. SAEM Thales. Sevilla. 49-53. •Alsina, C; Pérez, R y Ruiz, C. (1989). Simetría dinámica. Síntesis. Madrid. •Aytüre - Scheele, Z. (1989). Nueas ideas de Origami. Papiroflexia para grandes y pequeños. Everest. León •Bolt (1982) Mathematic activities. •Breda, Aart van ( ). Origami. El arte del papel plegado. Kapeñusz •Gardner, M. (1982). Nuevos pasatiempos matemáticos. Alianza. Madrid •Gardner, M.. (1987). Hexaflexágonos. Cacumen 44. 16-18 90
- 91. •Kasahara, K. (1993).Papiroflexia "Origami" creativa. Editor: Editorial Edaf, S.A. •Ledesma, A. (1992). Épsilon nº 24, 51-68 •Noda, M.A. y Plasencia, I. (2002). La matemática de los cuentos. Suma 41. 93 - 101. •Wenniger, J (1975). Matemática más fácil con anualidades de papel. Vanguardia pedagógica-distein. •Blanco, l. y Márquez, L. (1987). En torno al teorema de Pict: Una experiencia de Enseñanza de la Geometría. Números nº 16. Sociedad Canaria de Profesores de Matemáticas. Tenerife. 41-53. •Bolt, B. (1984). Mathematical activities. Cambridge. •Bolt, B. (1987). Divertimentos matemáticos. Labor. 91