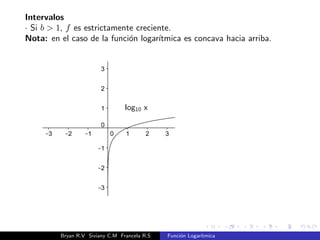
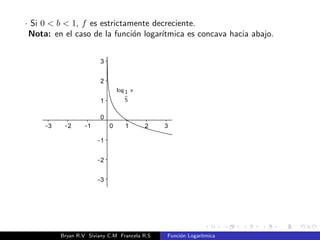
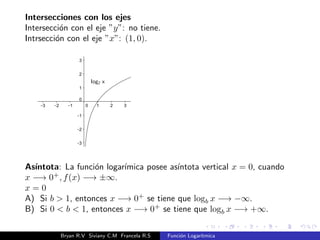
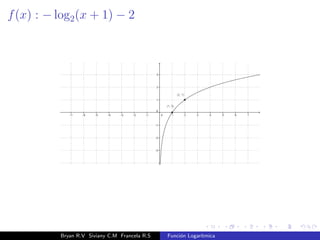
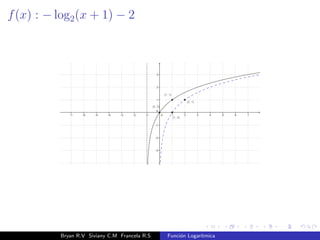
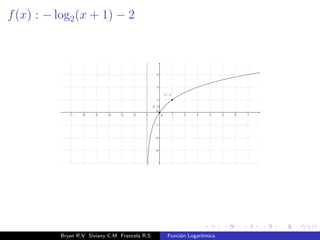
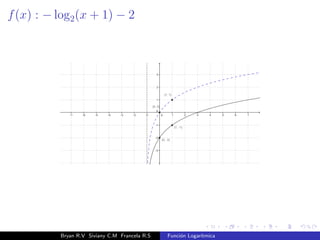
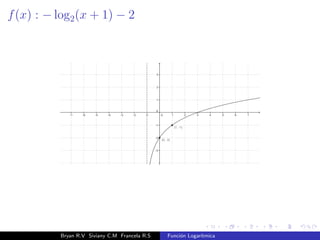
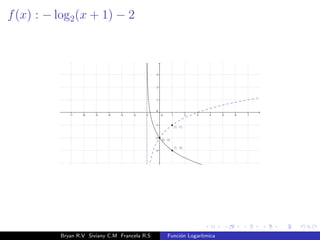
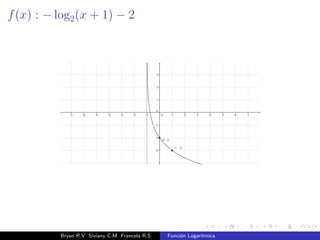
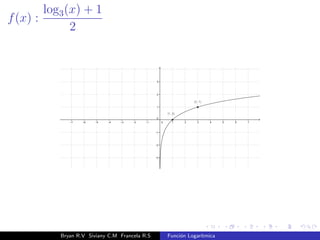
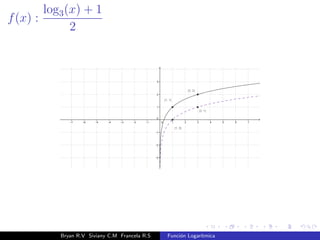
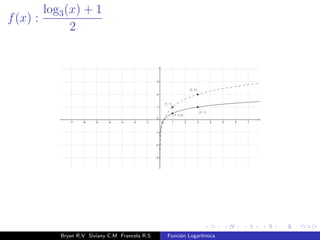
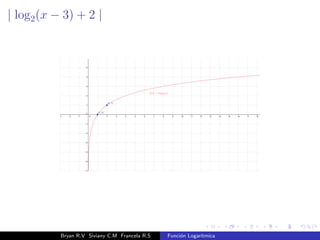
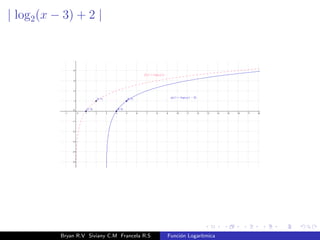
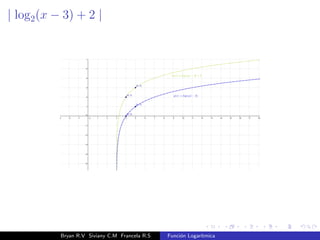
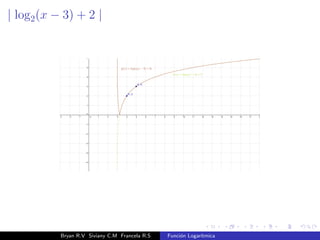
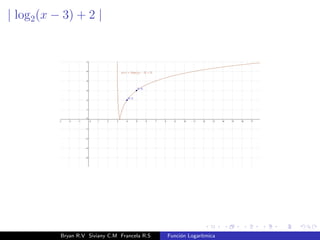
El documento presenta una introducción a la función logarítmica. Explica el contexto histórico de los logaritmos, su definición matemática, características como dominio, codominio y monotonía, propiedades como aditividad y aplicaciones a ecuaciones exponenciales. Finalmente, incluye ejercicios y contextos extra-matemáticos para ilustrar el uso de funciones logarítmicas.

1. Sede del Atlantico, UCR
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

2. Funcion Logartmica
Introduccion a la Matematica MA0123
Bryan R.V
Siviany C.M
Francela R.S
18 Octubre 2013
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

3. Contexto Historico.
Los logaritmos se inventaron alrededor de 1590 por John Napier
(1550-1617) y Jobst Burgi (1552-1632). Su enfoque de los logaritmos
era muy diferente al nuestro, se basaba en la relacion entre secuencias
aritmeticas y geometricas y no en la actual como funcion inversa
(recproca) de las funciones exponenciales.
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

4. Las tablas de Napier, publicadas en 1614, contenan los llamados
logaritmos naturales y eran algo difciles de usar. Un profesor londinense,
Henry Briggs, se intereso en las tablas y visito a Napier, Briggs convirtio
las tablas de Napier en las tablas de logaritmos comunes que fueron
publicadas en 1617.
Su importancia para el calculo fue inmediatamente reconocida y
alrededor de 1650 se impriman en lugares tan lejanos como China.
Dichas tablas siguieron siendo una poderosa herramienta de calculo hasta
el advenimiento de las calculadoras manuales de bajo precio alrededor de
1972.
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

5. De

6. nicion.
La funcion logartmica con base b; b 2 R+; b6= 1, la funcion
f : R+ ! R, de

7. nida por f(x) = logb x, donde:
logb x = y , by = x.
Logaritmo de un numero (x) es el exponente (y) al que hay que elevar la
base (b) para que nos de dicho numero (x), el numero x debe ser
positivo x 0.
logb x, see lee logartmo en base b de x.
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

8. Caractersticas
Criterio:La funcion logartmica es una funcion cuyo criterio es de la forma
f(x) = logb x, con b 2 R+, b 1 y x 0 . Se lee logartmo base b de
x. logb x = y , by = x
Dominio: R+.
Codominio: R.
Rango o Ambito: R.
Sea f : R+ ! R; f(x) : logb x
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

9. Monotona.
Teorema.
La funcion logartmica f : R+ ! R tal que f(x) = logb x, con
b 2 R+; b6= 1, entonces
i) Si b 1 f es creciente.
ii) Si 0 b 1 f es decreciente.
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

10. Sea f : R+ ! R con f(x) = logb x
i) Si b 1.
Sean x1; x2 2 R+ tal que x1 x2
f(x1) = y1 , logb x1 = y1 , by1 = x1 y
f(x2) = y2 , logb x2 = y2 , by2 = x2
Luego by1 by2 , como b 1
, y1 y2
, f(x1) f(x2)
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

11. Intervalos
Si b 1, f es estrictamente creciente.
Nota: en el caso de la funcion logartmica es concava hacia arriba.
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

12. Si 0 b 1, f es estrictamente decreciente.
Nota: en el caso de la funcion logartmica es concava hacia abajo.
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

13. Biyectividad
Decimos que una funcion f : A R ! R es monotona si y solo si es
creciente en A o decreciente en A. La funcion logartmica cumple lo
anterior dicho ya que f : R+ ! R y esta es creciente o decreciente,
entonces es monotona.
Por el teorema que dice Si f de

14. nida en A R es una funcion
monotona, entonces, considerando su ambito B como su codominio,
existe la funcion inversa f1 : B A.
Como la funcion logartmica es monotona, y su rango es igual al
codominio(f : R+ ! R), entonces existe la funcion inversa. Por lo
tanto, la funcion logartmica es biyectiva.
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

15. Inversa
Una funcion y su inversa cumplen las propiedades:
f1(f(x)) = x; 8x 2 Df y f(f1(x)) = x; 8x 2 Df1
La inversa de la funcion logartmica f(x) = loga x es la funcion
exponencial f1(x) = ax.
Si f(x) = loga x , f1(x) = ax, entonces:
A) (f f1)(x) = f(f1(x)) = loga(f1(x)) = loga ax = x, con x 2 R
B) (f1 f)(x) = f1(f(x)) = af(x) = aloga x = x, con x 0
) loga ax = aloga x
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

16. Intersecciones con los ejes
Interseccion con el eje y: no tiene.
Intrseccion con el eje x: (1; 0).
Asntota: La funcion logarmica posee asntota vertical x = 0, cuando
x ! 0+; f(x) ! 1.
x = 0
A) Si b 1, entonces x ! 0+ se tiene que logb x ! 1.
B) Si 0 b 1, entonces x ! 0+ se tiene que logb x ! +1.
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

17. Propiedades de los logaritmos.
A)loga(xy) = loga x + loga y.
B)loga
x
y
= loga(x y) = logb x loga y.
C)loga xn = n loga x.
D) loga x =
logb x
logb a
, b 0; b6= 1.
Pruebe que:
A)loga x
1
n = 1
n loga x.
B) loga
n p
x =
loga x
n
.
C)logb b = 1.
D)logb 1 = 0.
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

18. Notas en la resolucion de ecuaciones exponenciales aplicando
logartmos:
Recordemos las relaciones:
a) logb x = a , ba = x
b) logb x = logb y , x = y
bx = a
log bx = log a
x log b = log a
x =
log a
log b
:
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

19. Funcion logaritmo natural.
Sea x un numero real positivo. La funcion logaritmo natural, denotada
por ln x, se de

20. ne:
ln x = y , ey = x. (ln x se lee logaritmo natural de x).
Las funciones inversas cumplen:
f(f1(x)) = x y f1(f(x)) = x.
Como (x) = ex y f1(x) = ln x son inversas una de la otra, podemos
concluir que:
ln ex = x y eln x = x.
a) y = e2x5
ln y = In e2x5
ln y = 2x 5
5 + ln y = 2x
1
2
(5 + ln y) = x
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

21. b) Si se depositan P dolares al 8 por 100 de interes, compuesto de forma
continua, Cuanto tiempo tardara en doblarse el capital?
Pe0;08t = 2P
e0;08t = 2
0; 08t = ln 2
t =
ln 2
0; 08
8; 66
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

22. Ejercicios:
A)log2 8 + log3 27 + log5 125 =
B)
1
2
log2 36 + log2
2
3
=
C)
1
2
log2 A + log2 B log2 C log2 D =
D)log3
A2 B5
p
C
D3
!
=
E)
x
p
x
3 p
x2 y z5
!
=
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

23. f(x) : log2(x + 1) 2
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

24. f(x) : log2(x + 1) 2
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

25. f(x) : log2(x + 1) 2
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

26. f(x) : log2(x + 1) 2
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

27. f(x) : log2(x + 1) 2
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

28. f(x) : log2(x + 1) 2
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

29. f(x) : log2(x + 1) 2
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

30. f(x) :
log3(x) + 1
2
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

31. f(x) :
log3(x) + 1
2
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

32. f(x) :
log3(x) + 1
2
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

33. j log2(x 3) + 2 j
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

34. j log2(x 3) + 2 j
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

35. j log2(x 3) + 2 j
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

36. j log2(x 3) + 2 j
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

37. j log2(x 3) + 2 j
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica

38. Contextos extra-matematicos: 1.Sitios para desperdicios peligrosos de
acuerdo con cifras seleccionadas de 1981 a 1995, el numero de sitios mas
profundos para desechos peligrosos en Estados Unidos se aproxima con la
funcion de

39. nida por:
f(x) = 11:34 + 317:01 log2 x
Bryan R.V Siviany C.M Francela R.S Funcion Logartmica