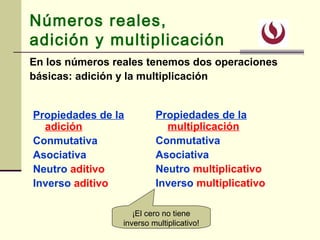
Este documento presenta los conceptos básicos de álgebra necesarios para economistas, incluyendo números reales, ecuaciones de primer y segundo grado. Explica las propiedades de la suma y multiplicación de números reales, y cómo resolver ecuaciones de primer grado y ecuaciones cuadráticas mediante el método de completar cuadrados o la fórmula general. El objetivo es que los estudiantes reconozcan estas herramientas y puedan aplicarlas para resolver problemas económicos.

1. Matemática Básica para
Economistas (MA99)
Unidad 1:Fundamentos de Álgebra
Sesión 1.1
Números reales, ecuaciones de
primer, segundo grado

2. Logros de la sesión
• El estudiante reconoce la similitud entre las operaciones de
suma y multiplicación de los reales y señala las cuatro reglas
básicas que cumplen.
• El estudiante identifica la relación de igualdad entre números
reales y la usa en la escritura de ecuaciones.
• El estudiante relaciona las reglas prácticas de resolución de
ecuaciones lineales y cuadráticas con las reglas básicas de los
números reales analizando los diferentes casos.
• El estudiante utiliza el método de completar cuadrados para
resolver ecuaciones cuadráticas.

3. Números reales
El menor valor
monetario que se
puede usar en una
transacción
comercial es un
céntimo de sol.
¿En qué conjunto
se pueden
encontrar los
valores monetarios
del nuevo sol
peruano usados
en las
transacciones
comerciales?

4. Números reales,
adición y multiplicación
Propiedades de la
adición
Conmutativa
Asociativa
Neutro aditivo
Inverso aditivo
En los números reales tenemos dos operaciones
básicas: adición y la multiplicación
Propiedades de la
multiplicación
Conmutativa
Asociativa
Neutro multiplicativo
Inverso multiplicativo
¡El cero no tiene
inverso multiplicativo!

5. Definiciones
1. Ecuación: Igualdad de dos expresiones
algebraicas.
2. Solución de una ecuación: Valor real de la
variable que verifica la ecuación.
3. Conjunto solución de una ecuación: Conjunto
de todas las soluciones de la ecuación (C.S.)
4. Ecuaciones equivalentes: Dos ecuaciones se
llaman equivalentes si tienen el mismo conjunto
solución.

6. Ecuación de primer
grado
Forma general:
Una ecuación de primer grado tiene una única
solución.
0,0 ≠=+ abax
:x :,baincógnita constantes

7. Ejemplos
1.
2.
3.
)3(25)1)(12( xxxx +−=−−
4
31
3
5
42
2
xx
x
−
−=
+
−
Raxax ∈+= ,52

8. Ecuaciones de segundo
grado
Ecuación cuadrática:
Teorema: Sean a y b números reales.
a.b = 0, si y solo si a = 0 ó b = 0
0,02
≠=++ acbxax
:x
:,ba
incógnita
constantes

9. 02)3(
059))3((
05)3()3()3(2
05)3(2
22
2
222
2
=−−
=+−−+
=+−−−+−+
=+−+
x
x
xx
xx
Método de resolución
Completando cuadrados
0562
=+− xx
222
2)( aaxxax ++=+
}1,5{..
0105
0)23)(23(
=
=−=−
=+−−−
SC
xox
xx

10. Ejercicios
01042.4 2
=+− xx
0127.2 2
=+− xx
054.1 2
=−− xx
384.3 2
=− xx

11. Método de resolución
Aspa simple
01272
=++ xx
.
Resuelva por el método de aspa simple la siguiente ecuación
Ejemplos
:
023.1 2
=++ xx
0143.2 2
=+− xx

12. Método de resolución
Fórmula General 002
≠=++ acbxax ,
Usando el método de completar cuadrados podemos
llegar a la fórmula general
acbD
a
Db
x 4,
2
2
2,1 −=
±−
=
D se conoce como el discriminante de la ecuación.

13. Ejemplos
0152.1 2
=++ xx
0144.2 2
=++ xx
04.3 2
=++ xx
¿Qué sucede con las soluciones x1 y x2 en cada ejemplo?