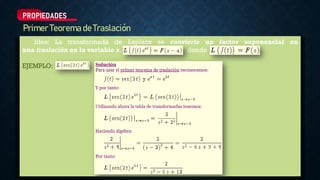
La transformada de Laplace es una técnica matemática útil para resolver ecuaciones diferenciales lineales no homogéneas convirtiéndolas en ecuaciones algebraicas. Se define como la integral de una función multiplicada por un exponencial negativo desde 0 hasta infinito. Tiene propiedades como la linealidad, que permite distribuir la transformada sobre sumas y restas, y teoremas como el de derivadas, que relaciona la derivada de una función con un factor multiplicativo en su transformada. La transformada de Laplace se usa comúnmente para resolver ecuaciones diferenciales con

1. Republica Bolivariana de Venezuela
Instituto Universitario Politécnico “Santiago Mariño”
Sede Barcelona
Escuela: Ingeniería de Sistemas
Asig: Matemáticas IV
Profesor:
Pedro Beltrán
Bachiller:
Jose Pereira
28.095.315
Barcelona, Agosto de 2019

2. La transformada de Laplace es un operador lineal muy
útil para la resolución de ecuaciones diferenciales.
Laplace demostró como transformar las ecuaciones
lineales no homogéneas en ecuaciones algebraicas
que pueden resolverse por medios algebraicos.
Cuando se resuelven ED usando la técnica de la
transformada, se cambia una ecuación diferencial en
un problema algebraico. La metodología consiste en
aplicar la transformada a la ED y posteriormente usar
las propiedades de la transformada. El problema de
ahora consiste en encontrar una función en la variable
independiente tenga una cierta expresión como
transformada.
Por lo general, para
denotar la función que se
desea trasformar se usan letras
minúsculas y la letra
mayúscula corresponde a su
trasformada. De esta manera
tendremos:

3. Sea f una función definida para la transformada
de Laplace de f(t) se define como:
Cuando tal integral converge.
Notas:
 La letra s representa una nueva variable, que para el proceso de integración se
considera constante
 La transformada de Laplace convierte una función en t en una función en la
variable s
 Condiciones para la existencia de la transformada de una función:
1. De orden exponencial
2. Continua a trozos

4. Si f(t) = c. Calcula su transformada de Laplace

5. Teorema
CONDICIONES DE EXISTENCIA
Si f es una función continua por parte para t > 0 y de
orden exponencial c, entonces existe la transformada de
Laplace para s > c.
Es importante resaltar que esta es una condición de
suficiencia, es decir que podría darse el caso en que exista
una función que no cumpla dichas condiciones y aun así su
transformada de Laplace exista.
Un ejemplo de esto es la función f(t) = t-1/2 que no
es continua por partes para t ≥ 0 pero su transformada
de Laplace existe.
1. Estar definida y ser
continua a pedazos en
el intervalo
2. Ser de orden
exponencial

6. Transformada de Laplace de algunas funciones básicas
En la siguiente tabla se muestran las transformadas
de Laplace de las funciones más comunes:

7. Linealidad
Idea: La transformada de Laplace se distribuye sobre las sumas o restas
y saca constantes que multiplican.
EJEMPLO:

8. Primer Teorema de Traslación
Idea: La transformada de Laplace se convierte un factor exponencial en
una traslación en la variable s. donde
EJEMPLO:

9. Teorema de la transformada de la derivada
Idea: La transformada de Laplace cancela la derivada multiplicando por la
variable s.
EJEMPLO:

10. Teorema de la transformada de la integral
EJEMPLO:

11. Teorema de la integral de la transformada
Siempre y
cuando exista
EJEMPLO:

12. Teorema de la derivada de la transformada
EJEMPLO:
C

13. Transformada de la función escalón
EJEMPLO:

14. Segundo teorema de Traslación
EJEMPLO:

15. Transformada de una función periódica

16. Teorema de la Convolución
Siempre y
cuando exista
EJEMPLO:

17. la transformada inversa de Laplace de una función F(s) es
la función f(t) que cumple con la propiedad
donde la L es la transformada de Laplace

18. Linealidad
PRIMERA PROPIEDAD DE TRANSLACION
SEGUNDA PROPIEDAD DE TRANSLACION

19. PROPIEDAD DEL CAMBIO DE ESCALA
TRANSFORMADA INVERSA DE LAPLACE EN LAS DERIVADAS
TRANSFORMADA INVERSA DE LAPLACE EN LAS INTEGRALES

20. MULTIPLICACIÓN POR S^N.
PROPIEDAD DE CONVOLUCIÓN.

21. Una de las principales aplicaciones de la transformada de Laplace es la de resolver
EDO con condiciones iniciales.
El método es esencialmente simple y puede ser descrito en los siguientes pasos.
1. Aplicar la transformada en ambos miembros de la EDO
2. Utilizar las propiedades de la transformada para que solo quede en términos
de L{y(t)} y despejarla. Lo que se obtiene recibe el nombre de ecuación algebraica o
subsidiaria.
3. Aplicar la transformada inversa para despejar y(t)

23. • Transformada Laplace. Extraído de:
http://www.ehu.eus/juancarlos.gorostizaga/apoyo/transform_lapl.htm
• Laplace. Extraído de:
https://previa.uclm.es/profesorado/raulmmartin/AmpliacionMatematicas/laplace.pdf
• Transformada de Laplace y sus aplicaciones a las ecuaciones diferenciales. Extraído
de: http://www.dmae.upct.es/~jose/varcomp/ctrans.pdf
• TRANSFORMADA DE LAPLACE. Extraído de:
http://www.mty.itesm.mx/etie/deptos/m/ma-841/laplace/