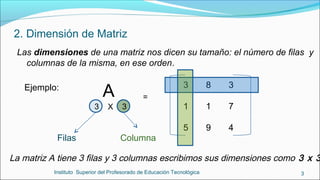
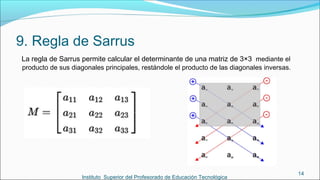
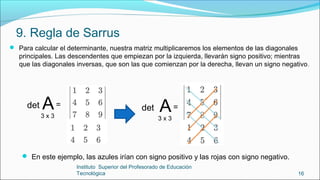
El documento presenta conceptos básicos sobre matrices, incluyendo su definición, dimensiones, elementos, tipos y operaciones como suma, producto y determinante. Explica que una matriz es una tabla de números ordenados en filas y columnas y define conceptos como fila, columna, elemento e índice. Luego describe tipos de matrices como cuadradas, rectangulares y nulas. Finalmente, detalla cómo realizar sumas, productos y cómo calcular el determinante, incluyendo la regla de Sarrus para matrices 3x3.

1. 1
Espacio Curricular: Matemática
Curso: 1 B
Carrera: Profesorado de Educación Tecnológica
Docente: Pestoni, Luis
Alumnos: Ceballos, Miriam
Moreno, Raul
Riesco, Ceferino
Schwarten, Jorge
Instituto Superior del Profesorado de Educación
Tecnológica

2. 1. Definición de Matriz
2Instituto Superior del Profesorado de Educación Tecnológica
“Una matriz es una tabla cuadrada o rectangular de datos o
elementos de números reales ordenados en filas y columnas,
donde una fila es cada una de las líneas horizontales de la matriz y
una columna es cada una de las líneas verticales de la matriz.”

3. 2. Dimensión de Matriz
3Instituto Superior del Profesorado de Educación Tecnológica
Ejemplo:
Las dimensiones de una matriz nos dicen su tamaño: el número de filas y
columnas de la misma, en ese orden.
3 3X
A
Filas Columna
3
1
5
8
1
9
3
7
4
=
La matriz A tiene 3 filas y 3 columnas escribimos sus dimensiones como 3 x 3

4. 4Instituto Superior del Profesorado de Educación Tecnológica
3. Notificación. Elementos de una Matriz
Un elemento de la matriz es una entrada de la tabla rectangular de datos ordenados.
Cada elemento se identifica al nombrar la fila y la columna en los cuales aparece.
3 X 3
A
3
1
5
8
1
9
3
7
4
=
Ejemplo
i
j
a 1
2
a
1 1 1 12 3
a2 1
a2 a2
3 2
a3 1
a3 a32 3
= 3a1 3
a a a
Indice
Subíndice
3 X 3
A =

5. • Matriz Rectangular
• Matriz Fila
• Matriz Nula
5Instituto Superior del Profesorado de Educación Tecnológica
• Matriz Cuadrada
• Matriz Columna
• Matriz Identidad
4. Tipo de Matrices
2 x 3
E
3
1
8
1
=
1 x 3
C 3 8 5=
2 x 2
F
0
0
0
0
=
3 x 3
A
3
1
5
8
1
9
3
7
4
=
3 x 1
B
3
1
5
=
3 x 3
D
1
0
0
0
1
0
0
0
1
=
5
3

6. SUMA y DIFERENCIA de Matrices
6
Instituto Superior del Profesorado de Educación
Tecnológica
5.2 Operaciones de Matrices. Suma y
Diferencia.
Para sumar o restar dos matrices sean A y B, se procede sumando o
restando los elementos de ambas que ocupan la misma posición.
8+0
1+1
9+0
3+0
7+0
4+0
+ = =
4
1
5
3
7
4;
C =
3 x 3
3 x 3
A
3
1
5
8
1
9
3
7
4
= D
1
0
0
0
1
0
0
0
1
=
3 x 3 3 x 3
A
;
D
3 x 3
3+1
1+0
5+0
8
2
9

7. 7
Instituto Superior del Profesorado de Educación
Tecnológica
5.2 Operaciones de Matrices. Producto
PRODUCTO de Matrices
Dos matrices A y B son multiplicables, si el mismo numero de columnas
de A coincide con el numero de filas de B. El elemento C del matriz
producto se obtiene multiplicando cada elemento la fila i de la matriz A por
cada elemento de la fila j de la matriz B y sumandolos.
B=
3 x 1
C
1 x 3
3 8 5= C B 3x3 + 8X1 + 5X5
x = = 42
3
1
5
C=
3 x 11 x 3 1 x 1
;
;

8. 8
Instituto Superior del Profesorado de Educación
Tecnológica
5.1 Ejercicio de Matrices. Suma y Producto
En el sector de Marketing de una empresa de Telecomunicaciones se está elaborando un registro de las ventas realizadas
de 3 (tres) marcas de equipos celulares en 2 (dos) sucursales, durante el período de Julio, Agosto y Septiembre, de los cuales
se necesita saber:
a) Las ventas totales en ambas sucursales por período y marcas de equipos.
b) La facturación total de las ventas en ambas sucursales, teniendo en cuenta las ventas por marca y su precio unitario.
Precio
Samsung LG Motorola Samsung LG Motorola Samsung 4300
Julio 1092 540 258 Julio 1820 728 364 LG 3250
Agosto 1452 650 330 Agosto 2880 987 459 Motorola 3180
Septiembre 890 380 185 Septiembre 1552 452 196
1092 540 258 1820 728 364 4300
A = 1452 650 330 B = 2880 987 459 E = 3250
890 380 185 1552 452 196 3180
Sucursal Capitalinas Sucursal Nuevocentro
3x13x3 3x3
1 2 3

9. PASO 1. SUMA de Matrices
9
Instituto Superior del Profesorado de Educación
Tecnológica
5.3 Resolución de Ejercicio de Matrices. Excel
PASO 2. PRODUCTO de Matrices
Función SUMA
Función MMULT

10. 6. Propiedades de la Suma de Matrices
Instituto Superior del Profesorado de Educación Tecnológica 10

11. 7. Propiedades de Producto de Matrices
Instituto Superior del Profesorado de Educación Tecnológica
11

12. 8. Determinante de una Matriz Cuadrada
 Llamamos determinante de A, det A, al número obtenido al sumar todos los diferentes productos de n elementos
que se pueden formar con los elementos de dicha matriz, de modo que en cada producto figuren un elemento de
cada distinta fila y uno de cada distinta columna, a cada producto se le asigna el signo (+) si la permutación de los
subíndices de filas es del mismo orden que la permutación de los subíndices de columnas, y signo (-) si son de
distinto orden.
Instituto Superior del Profesorado de Educación Tecnológica 12
 El DETERMINANTE en una matriz cuadrada cualquiera A mxn, es una operación que se
realiza sobre matrices cuadradas cuyo resultado es un número real.

13. 8. Determinante de una Matriz Cuadrada.
Para una matriz de orden 2, su determinante se calcula:
Instituto Superior del Profesorado de Educación Tecnológica
13
Cada producto tiene que estar formado por un elemento de la primera fila y un elemento de la segunda fila, pero al mismo
tiempo tienen que ser un elemento de la primera columna y un elemento de la segunda. Sólo hay dos emparejamientos
posibles, los que están arriba indicados. En cuanto al signo de cada producto, si los ordenamos siempre según el orden
de las filas nos debemos fijar en el orden de las columnas (los segundos índices) de cada agrupación, nosotros lo hemos
indicado debajo entre corchetes. Como el primer producto representa una permutación par su signo es positivo, en
cambio en el segundo es impar y es negativo

14. 9. Regla de Sarrus
La regla de Sarrus permite calcular el determinante de una matriz de 3×3 mediante el
producto de sus diagonales principales, restándole el producto de las diagonales inversas.
Instituto Superior del Profesorado de Educación Tecnológica
14

15. 9. Regla de Sarrus.
 Si tomamos una matriz 3×3 cualquiera por ejemplo
Instituto Superior del Profesorado de Educación Tecnológica
15
Para aplicar la regla de Sarrus, y resolverla de un modo más visual, deberíamos incluir la fila 1 y
2, como fila 4 y 5 respectivamente. Es importante mantener la fila 1 en la 4ª posición, y la fila 2 en
la 5ª. Ya que si las intercambiamos, la Regla de Sarrus no resultará efectiva.
A=
3 x 3

16. 9. Regla de Sarrus
Instituto Superior del Profesorado de Educación
Tecnológica 16
 Para calcular el determinante, nuestra matriz multiplicaremos los elementos de las diagonales
principales. Las descendentes que empiezan por la izquierda, llevarán signo positivo; mientras
que las diagonales inversas, que son las que comienzan por la derecha, llevan un signo negativo.
 En este ejemplo, las azules irían con signo positivo y las rojas con signo negativo.
A=
3 x 3
A=
3 x 3
det det

17. 9. Regla de Sarrus
 El cálculo final de la Regla de Sarrus quedaría de esta manera:
Instituto Superior del Profesorado de Educación Tecnológica 17
A=
3 x 3
det
A=det 0

18. 18
GRACIAS
Instituto Superior del Profesorado de Educación Tecnológica