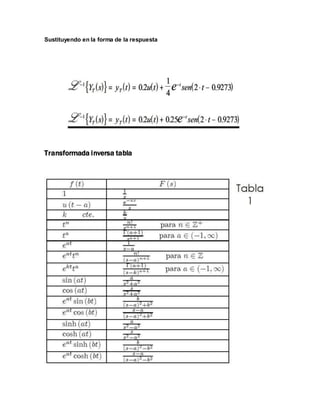
Este documento presenta la transformada de Laplace, una herramienta matemática utilizada para resolver ecuaciones diferenciales ordinarias. Explica la definición formal de la transformada de Laplace y provee ejemplos como la función de Heaviside y la función exponencial. Luego, muestra cómo aplicar la transformada de Laplace para resolver una ecuación diferencial lineal de segundo orden con condiciones iniciales. Finalmente, introduce la transformada inversa y cómo usarla para obtener la solución original de la ecuación diferencial.

1. PROFESORA BACHILLER
RANIELINA RONDÓN. JOHAN ALCALÁ
C.I: 25.060.699
Puerto la cruz 06/07/16
INSTITUTO UNIVERSITARIO DE TECNOLOGÍA
“ANTONIO JOSÉ DE SUCRE”
EXTENSIÓN BARCELONA - PUERTO LA CRUZ
MENCIÓN: MECÁNICA MANTENI MIENTO

2. La transformada de Laplace
La transformada de Laplace es un tipo de transformada integral frecuentemente usada para la
resolución de ecuaciones diferenciales ordinarias. La transformada de Laplace de
una función f(t) definida (en ecuaciones diferenciales, en análisis matemático o en análisis
funcional) para todos los números positivos t ≥ 0, es la función F(s),
Sea f una función definida para , la transformada de Laplace de f(t) se define
como:
Ejemplos
Función de Heaviside. Sea a≥ 0 y consideremos la función de Heaviside ha definida
anteriormente. Entonces para todo z ∈ C tal que Re Z > 0 se verifica
Función exponencial: Sea ω∈ C y consideremos la función exponencial f(t)=eωt . Se
verifica entonces para todo Z ∈ C tal que Re Z> Re ω

3. Ejemplos
Aplicación de Transformada de Laplace
La Transformada de Laplace es una herramienta útil para resolver ecuaciones y
sistemas de ecuaciones diferenciales lineales con coeficientes constantes. Como
comentamos en la introducción del tema, estas ecuaciones aparecen de forma natural en
la teoría de circuitos eléctricos. Para ilustrar el método, consideremos el siguiente
ejemplo: la ecuación
𝑦 𝑛 + y = cos 𝑡 (1.2)
Junto con las condiciones iniciales
y(0) = 0; y0 (0) = 1. (2.2)
Básicamente se trata de aplicar la Transformada de Laplace y sus propiedades a (2.1) de
manera que teniendo en cuenta (2.2), nuestro problema se convierte en el problema
algebraico

4. Una vez obtenida L[y], hemos de usar la Transformada inversa para volver atrás y
recuperar la solución del problema y. En este caso, L[y] satisface las condiciones del
Teorema 14, por lo que

5. La Transformada inversa
La Transformada inversa: de una función en s, digamos F(s) es una función de t cuya
transformada es precisamente F(s), es decir
si es que acaso
Esta definición obliga a que se cumpla:
y
Aplicando Transformada Inversa
Hallando coeficientes

6. Sustituyendo en la forma de la respuesta
Transformada inversa tabla

7. Ejemplos