Este documento describe el método de la bisección para encontrar raíces de una ecuación. El método involucra iterativamente dividir el intervalo inicial en dos partes iguales basado en si el valor de la función es positivo o negativo en el punto medio, hasta que el intervalo sea menor a un error especificado. El documento provee detalles sobre cómo calcular el número de iteraciones necesarias y presenta un ejemplo numérico para ilustrar el método.

1. MÉTODO DE LA BISECCIÓN
CLASE 3

2. MÉTODO DE LA BISECCIÓN
• El método de la bisección es muy similar al de la posición falsa,
aunque algo mas simple. Como en el de la posición falsa, en
este método también se requieren dos valores iniciales para
ambos lados de la raíz, y que sus valores funcionales
correspondientes sean de signos opuestos.

3. MÉTODO DE LA BISECCIÓN
• En este caso, el valor de 𝑥 𝑚 se obtiene como el punto medio entre
𝑥𝑙 𝑦 𝑥 𝑑
• 𝑥 𝑚 = 𝑥𝑙 + 𝑥 𝑑 /2
• Dependiendo de la función que se tenga en particular, el método de
la bisección puede converger ligeramente mas rápido o mas lento
que el método de la posición falsa. Su gran ventaja sobre el de
posición falsa es que proporcionan el tamaño exacto del intervalo en
cada iteración (en ausencia en errores de redondeo).

4. MÉTODO DE LA BISECCIÓN
• Para aclarar esto, nótese que en este método, después de cada
iteración, el tamaño del intervalo se reduce a la mitad, después de n
iteraciones, el intervalo original se habrá reducido 2 𝑛 veces.
• Por lo anterior, si el intervalo original es del tamaño 𝑎 y el criterio de
convergencia aplicado al valor absoluto de la diferencia de dos 𝑥 𝑚
consecutivas es 𝜀, entonces se requerirán 𝑛 iteraciones, donde 𝑛 se
calcula con la igualdad de la expresión:
• 𝑎
2 𝑛 ≤ 𝜀

5. MÉTODO DE LA BISECCIÓN
• De donde
• 𝑛 =
ln 𝑎 −ln 𝜀
ln 2
• Por esto se dice que se puede saber de antemano cuantas
iteraciones se requieren.

6. CONVERGENCIA DEL MÉTODO DE LA
BISECCIÓN
• Algoritmo del método de la bisección
• Calcular una raíz 𝑟 real de la ecuación 𝑓 𝑥 𝑚 = 0 con
precisión 𝐸. 𝑓 es continua en un intervalo 𝑥𝑙, 𝑥 𝑑 tal
que 𝑓 𝑥𝑙 𝑦 𝑓(𝑥 𝑑) tienen signos diferentes.
1. Defina 𝑓, el intervalo inicial 𝑥𝑙, 𝑥 𝑑 y la precisión
requerida 𝐸
2. Calcule el punto central del intervalo: 𝑥 𝑚 = (𝑥𝑙 + 𝑥 𝑑)/2

7. CONVERGENCIA DEL MÉTODO DE LA
BISECCIÓN
3. Si 𝑓 𝑐 = 0, 𝑐 es la raíz y termine.
4. Si la raíz se encuentra en el intervalo 𝑥𝑙, 𝑥 𝑚 ,
sustituya 𝑏 𝑝𝑜𝑟 𝑐
5. Si la raíz se encuentra en el intervalo 𝑥 𝑚, 𝑥 𝑑 sustituya
𝑎 𝑝𝑜𝑟 𝑐
6. Repita los pasos 2, 3, 4 y 5 hasta que la longitud del
intervalo 𝑥𝑙, 𝑥 𝑑 sea menor que 𝐸.

8. CONVERGENCIA DEL MÉTODO DE LA
BISECCIÓN
•El ultimo valor calculado 𝑐 estará al menos a
una distancia 𝐸 de la raíz.

9. EJEMPLO DEL MÉTODO DE LA BISECCIÓN
• Utilice el método de la bisección para obtener una raíz del
polinomio
• 𝑓 𝑥 = 𝑥3
+ 2𝑥2
+ 10𝑥 − 20

10. SOLUCIÓN
• Primero graficamos en Matlab para verificar donde existen los
cambios de signo y establecer nuestro intervalo de análisis

11. SOLUCIÓN
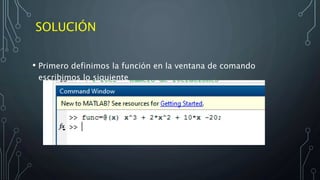
• La función MATLAB fzero
• La función fzero puede encontrar la raíz de una ecuación trascendente 𝑓(𝑥) = 0.
Su sintaxis es
• fzero(funcion,x0)
• Donde función es el nombre de la función cuyas raíces queremos determinar y
𝑥0 es el intervalo [𝑎, 𝑏] donde la función cambia de signo, es decir, el signo de
𝑓(𝑎) es distinto al signo de 𝑓(𝑏). 𝑥0 puede ser también un valor cercano a la raíz
es decir, una primera aproximación. Podemos definir una función anónima y
guardarla en el manejador func. Le pasamos la función anónima func a fzero.

12. SOLUCIÓN
• Paso 1
• Introducimos lo siguiente en la ventana de comando de Matlab
• func=@(x) x^3 + 2*x^2 + 10*x -20;
• ezplot(func,[0,4])

13. SOLUCIÓN

14. SOLUCIÓN
• Lo que da el siguiente
resultado
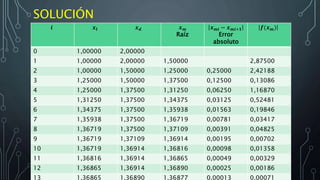
• Podemos observar que
entre el intervalo [1,2]
existe un cambio de signo
en 𝑦

15. SOLUCIÓN
• Con los valores iniciales obtenidos en el Matlab establecemos
el intervalo de análisis
• 𝑥𝑙 = 1; 𝑓 𝑥𝑙 = 𝑥3 + 2𝑥2 + 10𝑥 − 20 →
• 𝑓 1 = 1 3 + 2 1 2 + 10(1) − 20
• 𝑓 1 = −7

16. SOLUCIÓN
• Con los valores iniciales obtenidos en el Matlab establecemos
el intervalo de análisis
• 𝑥 𝐷 = 1; 𝑓 𝑥 𝐷 = 𝑥3 + 2𝑥2 + 10𝑥 − 20 →
• 𝑓 2 = 2 3 + 2 2 2 + 10(2) − 20
• 𝑓 2 = 16

17. SOLUCIÓN
• Si 𝜀 = 10−3, el numero de iteraciones 𝑛 será
• 𝑛 =
ln 𝑎 −ln 𝜀
ln 2
=
ln 2−1 −ln(10−3)
ln 2
= 9,96
• Ó bien
• 𝑛 ≈ 10

18. SOLUCIÓN
• Primera iteración
• 𝑥 𝑚 = 𝑥𝑙 + 𝑥 𝑑 /2
• 𝑥 𝑚 =
1+2
2
= 1,5, 𝑓 𝑥 𝑚 = 𝑥3 + 2𝑥2 + 10𝑥 − 20
• 𝑓 1.5 = (1.5)3
+2(1.5)2
+10(1.5) − 20
• 𝑓 1.5 = 2,88

19. SOLUCIÓN
• Como 𝑓 𝑥 𝑚 > 0 se reemplaza el valor de 𝑥 𝑑 con el de 𝑥 𝑚, con lo
cual queda un nuevo intervalo (1,1,5). Entonces:
• 𝑥𝑙 = 1; 𝑓 𝑥 𝑑 = −7
• 𝑥 𝑑 = 1,5; 𝑓 𝑥 𝑑 = 2.88

20. SOLUCIÓN
• Segunda iteración
• Se reemplaza el valor de 𝑥 𝑑 con el valor de la nueva 𝑥 𝑚
• 𝑥 𝑚 = 𝑥𝑙 + 𝑥 𝑑 /2
• 𝑥 𝑚 =
1+1.5
2
= 1.25, 𝑓 𝑥 𝑚 = 𝑥3
+ 2𝑥2
+ 10𝑥 − 20
• 𝑓 1.25 = (1.25)3
+2(1.25)2
+10(1.25) − 20
• 𝑓 1.25 = −2.42

21. SOLUCIÓN
• Como ahora 𝑓 𝑥 𝑚 < 0 se reemplaza el valor de 𝑥𝑙 con el valor
de la nueva 𝑥 𝑚; de esta manera queda como intervalo 1.25, 1.5

22. SOLUCIÓN
• Tercera iteración
• Se reemplaza el valor de 𝑥𝑙 con el valor de la nueva 𝑥 𝑚
• 𝑥 𝑚 = 𝑥𝑙 + 𝑥 𝑑 /2
• 𝑥 𝑚 =
1,25+1,5
2
= 1.375, 𝑓 𝑥 𝑚 = 𝑥3
+ 2𝑥2
+ 10𝑥 − 20
• 𝑓 1.375 = (1.375)3+2(1.375)2+10(1.375) − 20
• 𝑓 1.375 = 2,599609375 + 3,78125 + 13,75 − 20 → 𝑓 1.125 = 0,130859375

23. SOLUCIÓN
• Como ahora 𝑓 𝑥 𝑚 > 0 se reemplaza el valor de 𝑥 𝑑 con el valor
de la nueva 𝑥 𝑚 ; de esta manera queda como intervalo
1.25, 1.375

24. SOLUCIÓN
• Cuarta iteración
• Se reemplaza el valor de 𝑥 𝑑 con el valor de la nueva 𝑥 𝑚
• 𝑥 𝑚 = 𝑥𝑙 + 𝑥 𝑑 /2
• 𝑥 𝑚 =
1,25+1,375
2
= 1,3125, 𝑓 𝑥 𝑚 = 𝑥3
+ 2𝑥2
+ 10𝑥 − 20
• 𝑓 1.25 = (1,3125)3
+2(1,3125)2
+10(1,3125) − 20
• 𝑓 1.25 = 2,260986328125 + 3,4453125 + 13,125 − 20 →
• 𝑓 1,25 = −1,168701171875

25. SOLUCIÓN
• Como ahora 𝑓 𝑥 𝑚 < 0 se reemplaza el valor de 𝑥𝑙 con el valor
de la nueva 𝑥 𝑚 ; de esta manera queda como intervalo
1,31250, 1.375

26. SOLUCIÓN
• La tabla muestra los cálculos llevados a cabo 13 veces, a fin de
hacer ciertas observaciones.

27. SOLUCIÓN
𝒊 𝒙𝒍 𝒙 𝒅 𝒙 𝒎
Raíz
𝒙 𝒎𝒊 − 𝒙 𝒎𝒊+𝟏
Error
absoluto
𝒇(𝒙 𝒎)
0 1,00000 2,00000
1 1,00000 2,00000 1,50000 2,87500
2 1,00000 1,50000 1,25000 0,25000 2,42188
3 1,25000 1,50000 1,37500 0,12500 0,13086
4 1,25000 1,37500 1,31250 0,06250 1,16870
5 1,31250 1,37500 1,34375 0,03125 0,52481
6 1,34375 1,37500 1,35938 0,01563 0,19846
7 1,35938 1,37500 1,36719 0,00781 0,03417
8 1,36719 1,37500 1,37109 0,00391 0,04825
9 1,36719 1,37109 1,36914 0,00195 0,00702
10 1,36719 1,36914 1,36816 0,00098 0,01358
11 1,36816 1,36914 1,36865 0,00049 0,00329
12 1,36865 1,36914 1,36890 0,00025 0,00186
13 1,36865 1,36890 1,36877 0,00013 0,00071

28. SOLUCIÓN
• Utilizamos el Matlab para comprobar nuestro calculo

30. SOLUCIÓN
• Primero definimos la función en la ventana de comando
escribimos lo siguiente