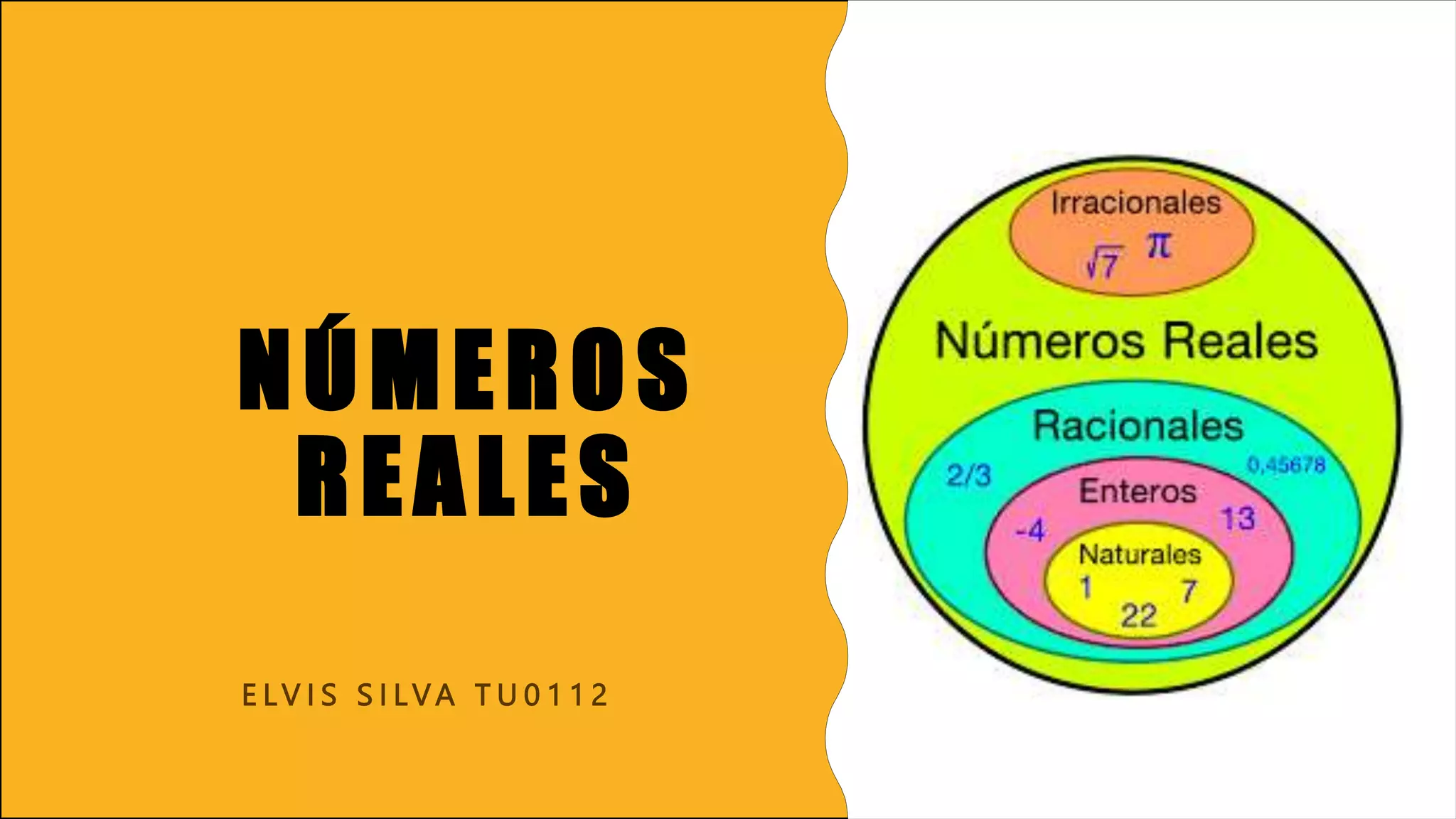
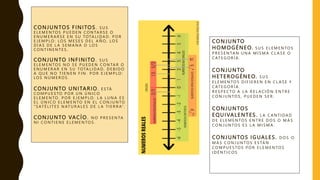
El documento define los conceptos básicos de conjuntos, incluyendo tipos de conjuntos como finitos, infinitos, unitarios, vacíos, homogéneos y heterogéneos. También describe operaciones con conjuntos como unión, intersección, diferencia, complemento y diferencia simétrica. Finalmente, introduce conceptos sobre números reales, incluyendo racionales e irracionales, y propiedades de desigualdades y valor absoluto.

1. NÚMEROS
REALES
E LV I S S I LVA T U 0 1 1 2

2. DEFICION DE CONJUNTOS
• Un conjunto es la agrupación de diferentes elementos
que comparten entre sí características y propiedades
semejantes. Estos elementos pueden ser sujetos u
objetos, tales como números, canciones, meses,
personas, etc. Por ejemplo: el conjunto de números
primos o el conjunto de planetas del sistema solar.
Tipos de conjuntos
A la hora de formar un conjunto, la manera y el porqué de la
agrupación de los elementos que lo conforman puede variar
dando lugar a diferentes tipos de conjuntos, que pueden ser:

3. CONJUNTOS FINITOS. S U S
E L E M E N TO S P U E D E N C O N TA R S E O
E N U M E R A R S E E N S U TOTA L I DA D. P O R
E J E M P LO : LO S M E S E S D E L A Ñ O, LO S
D Í A S D E L A S E M A N A O LO S
C O N T I N E N T E S .
CONJUNTO INFINITO. S U S
E L E M E N TO S N O S E P U E D E N C O N TA R O
E N U M E R A R E N S U TOTA L I DA D, D E B I D O
A Q U E N O T I E N E N F I N . P O R E J E M P LO :
LO S N Ú M E R O S .
CONJUNTO UNITARIO . E S TÁ
C O M P U E S TO P O R U N Ú N I C O
E L E M E N TO. P O R E J E M P LO : L A L U N A E S
E L Ú N I C O E L E M E N TO E N E L C O N J U N TO
“ S AT É L I T E S N AT U R A L E S D E L A T I E R R A”.
CONJUNTO VACÍO. N O P R E S E N TA
N I C O N T I E N E E L E M E N TO S .
CONJUNTO
HOMOGÉNEO. S U S E L E M E N TO S
P R E S E N TA N U N A M I S M A C L A S E O
C AT E G O R Í A .
CONJUNTO
HETEROGÉNEO. S U S
E L E M E N TO S D I F I E R E N E N C L A S E Y
C AT E G O R Í A .
R E S P E C TO A L A R E L A C I Ó N E N T R E
C O N J U N TO S , P U E D E N S E R :
CONJUNTOS
EQUIVALENTES. L A C A N T I DA D
D E E L E M E N TO S E N T R E D O S O M Á S
C O N J U N TO S E S L A M I S M A .
CONJUNTOS IGUALES. D O S O
M Á S C O N J U N TO S E S TÁ N
C O M P U E S TO S P O R E L E M E N TO S
I D É N T I C O S

4. OPERACIONES CON CONJUNTOS
• Los objetos de un conjunto pueden ser cualquier cosa siempre que tengan una relación entre ellos, a los
objetos de un conjunto se les llama elementos de dicho conjunto, por lo tanto un conjunto contiene a
sus elementos Se representan con una letra mayúscula y a los elementos o miembros de ese conjunto se
les mete entre llaves corchetes o paréntesis. ({,}).
• Unión: El símbolo del operador de esta
operación es: ∪, y es llamado copa.
• Es correspondiente a la formación de los
elementos de dos conjuntos o incluso más
conjuntos que pueden, partiendo de esto
conformar una nueva forma de conjunto, en la
cual los elementos dentro de este
correspondan a los elementos de los conjuntos
originales.
• Sean A y B dos conjuntos, la junta de ambos
(A ∪ B) es el conjunto C el cual contiene a
todos los elementos pertenecientes
al conjunto A o al conjunto B.
• Ejemplo: La unión de los conjuntos A={1,2,3} y
B={4,5,6} sería el conjunto C={1,2,3,4,5,6}, esto
es: {1,2,3}∪{4,5,6}={1,2,3,4,5,6}
Intersección:
El símbolo del operador de esta operación es: ∩, y
es llamado capa.
Sean A y B dos conjuntos, la coincidencia de
ambos (A ∩ B) es el conjunto C el cual contiene los
elementos que están en A y que están en B.
Un elemento x pertenece a la coincidencia de los
conjuntos A y B si, y sólo si, x pertenece al
conjunto A y x pertenece al conjunto B a la vez, por
lo tanto
Disjuntividad
Se dice que dos conjuntos A y B son disjuntos
cuando la coincidencia de ambos es el conjunto
vacío. A ∩ B=
Ejemplo: La coincidencia de A={3,7,8} y B={1,2,9}
sería C=∅ ya que {3,7,8}∩{1,2,9}=∅ por lo tanto A y
B son disjuntos.
.

5. • Diferencia: El símbolo de esta operación es: .
• La diferencia consiste en eliminar de A todo
elemento que esté en B, también se puede
denotar con el símbolo de la resta A-B, por lo
tanto, la diferencia de los conjuntos A y B es el
conjunto C que tiene a todos los elementos que
están en A, pero no en B.
• Por lo tanto, un elemento pertenece a la
diferencia de A y B si, y sólo si
• Ejemplo: La diferencia de los conjuntos A
{1,2,3,4} y B {1,3,5,7} es el conjunto C {2,4}, sin
embargo la diferencia de los conjuntos B
{1,3,5,7} y A {1,2,3,4} es el conjunto C{5,7}.
Complemento: El símbolo de esta operación es: A∁,
o también se suele representar con el símbolo A
Supongamos que U es el conjunto universal, en el cual
se encuentran todos los elementos posibles, entonces
el complementario de A con respecto a U se consigue
restando a U todos los elementos de A.
Ejemplo: El complementario del conjunto de todos los
números positivos mayores de 5 incluyendo el 5, es el
conjunto {1,2,3,4}
Diferencia Simétrica :La diferencia simétrica de dos
conjuntos A y B es otro conjunto el cual posee los
elementos que o bien se encuentran en A, o bien se
encuentran en B, pero no en los dos a la vez. A Δ B = C,
donde C no tiene
Ejemplo: La diferencia simétrica del conjunto de personas
que juegan a fútbol y el conjunto de personas que juegan
a baloncesto es el conjunto de personas que juegan sólo a

6. • Producto cartesiano
• En un conjunto los elementos están desordenados y el orden es muy importante, por ello necesitamos algún
tipo de estructura diferente para representar a los elementos ordenados, de ahí salen las n-tuplas ordenadas.
• La n-tupla ordenada es la colección ordenada dónde su primer elemento es es su
segundo elemento, el elemento n-ésimo.
• El producto cartesiano de dos conjuntos A y B es el conjunto C, C = A × B, donde los pares ordenados (a,b)
están formados por un primer elemento perteneciente a A y un segundo elemento perteneciente a B.
• Ax
Ejemplo: El producto cartesiano de A={2,3} y B={a,b,c} es A×B={(2,a),(2,b),(2,c),(3,a),(3,b),(3,c)}
Principio de inclusión-exclusión
Es la generalización del resultado de las uniones de un número arbitrario de conjuntos, es una técnica muy
importante que se usa principalmente en los problemas de enumeración.
Sucede por ejemplo cuando queremos encontrar un cardinal de la unión de dos conjuntos y para encontrar dicho
número de la unión de dos conjuntos finitos A y B, hay que tener en cuenta que en A∪B cada elemento de A está
solo una vez en A, pero no en B, y viceversa, pero hay algunos elementos que pueden pertenecer a A y a B a la vez,
por lo tanto el principio de inclusión-exclusión se basa en restar a la unión de dos conjuntos finitos la intersección
de ambos.
Matematicamente: A∪B - A∩B

7. NUMERO REALES
Números Reales
Se puede definir a los números reales como
aquellos números que tienen expansión decimal
periódica o tienen expansión decimal no
periódica. Por ejemplo)
a) 3 es un número real ya que 3 =
3,00000000000….b)
b) ½ es un número real ya que ½ =
0,5000000000….
c) 1/3 es un número real y que 1/3 =
0,3333333333333….
d) 2es un número real ya que 2=
e)1,4142135623730950488016887242097….e)0,12
34567891011121314151617181920212223…. Es
un número real)
f) 1,01001000100001000001000000100000001….)
g) π también es real
• Como puede verse algunos tienen expansión
decimal periódica a, b y c y otros tienen expansión
decimal no periódica d, e, f y g. Los números que
tienen expansión decimal periódica se llaman
números Racionales (denotados por Q) y los
números que tienen expansión decimal no
periódica se llaman Irracionales (denotados por I).
En consecuencia a, b y c son números racionales y
d, e, f y g son números irracionales . Claramente, la
propiedad de tener expansión decimal periódica
para los racionales y la propiedad de tener
expansión decimal no periódica para los
irracionales define dos tipo de números muy
distintos. Lo que significa que un número real es
racional o irracional, nunca ambos.

8. • Conjunto de números reales:
De acuerdo a lo anteriormente expuesto, el conjunto de los
números reales se define como la unión de dos tipos de
números, a saber; los números racionales, los números
irracionales a su vez, los números racionales se clasifican en:
a) Números Naturales (N), los que usamos para contar. Por
ejemplo, 1, 2, 3, 4, 5,6, 7, 8, 9, 10, 11, …
b)Números Enteros (Z), son los números naturales, sus
negativos y el cero. Por ejemplo: -3, -2, -1, 0, 1, 2, 3,…
c) Números Fraccionarios, son aquellos números que se
pueden expresar como cociente de dos números enteros, es
decir, son números de la forma a/b Con a,b enteros y b ≠ 0.
d)Números Algebraicos, son aquellos que provienen de la
solución de alguna ecuación algebraica y se representan por un
número finito de radicales libres o anidados.
Propiedades de los números reales
Propiedad : Conmutativa
Operación: Suma y Resta
Definición: a+b = b+a Ejemplo:2+8 = 8+2 5(-3) = ( -3)5
Propiedad: Asociativa
Operación: Suma y Multiplicación
Definición: a+(b+c)=(a+b)+c------ a(bc) = (ab)c
Que dice : Puedes hacer diferentes asociaciones al sumar
o multiplicar reales y no se afecta el resultado.
Ejemplo:7+(6+1)=(7+6)+1 -2(4x7)= (-2x4)
Propiedad: Identidad
Operación: Suma y Multiplicación
Definición: a + 0 = a------ a x 1= a
Que dice: Todo real sumado a 0 se queda
igual; el 0 es la identidad aditiva. Todo real
multiplicado por 1 se queda igual; el 1 es la
identidad multiplicativa.
Ejemplo:-11 + 0 = -11 17 x 1 =17
Propiedad: Distributiva
Operación : Suma respecto a Multiplicación
Definición: a (b + c) = ab + a c
Que dice : El factor se distribuye a cada sumando.Ejemplos:2(x+8)
= 2(x) + 2(8)

9. DESIGUALDADES
Inecuaciones y desigualdades
Las inecuaciones son desigualdades algebraicas en
la que sus dos miembros se relacionan por uno de
estos signos:
< Menor que 2x − 1 < 7
≤ Menor o igual que 2x − 1 ≤ 7
> Mayor que 2x − 1 > 7
≥ Mayor o igual que 2x − 1 ≥ 7
La solución de una inecuación es el conjunto de
valores de la variable que la verifica
La solución de la inecuación se expresa mediante:1. Una
representación gráfica.2. Un intervalo.
2x − 1 < 7
2x < 8 x < 4
(-∞, 4)
2x − 1 ≤
2x≤ 8 x ≤ 4
(-∞, 4]
2x − 1 > 7
2x > 8 x > 4

10. Inecuaciones equivalentes
Si a los dos miembros de una inecuación se les suma o se les
resta un mismo número, la inecuación resultante es
equivalente a la dada.
3x + 4 < 5 3x + 4 − 4 < 5 − 4 3x <
1Si a los dos miembros de una inecuación se les multiplica o
divide por un mismo número positivo, la inecuación
resultante es equivalente ala dada
2x < 6 2x : 2 < 6 : 2 x < 3
Inecuaciones de primer grado
Inecuaciones de primer grado con una incógnita
1º Quitar corchetes y paréntesis.
2º Quitar denominadores.
3º Agrupar los términos en x a un lado de la desigualdad y los
términos independientes en el otro.
4º Efectuar las operaciones
5ºSi el coeficiente de la x es negativo multiplicamos por −1,
por lo
que cambiará el sentido de la desigualdad.
6º Despejamos la incógnita.
7º Expresar la solución de forma gráfica y con un intervalo
[3, +∞)
Inecuaciones de segundo grado
Consideremos la inecuación:x2− 6x + 8 > 0
La resolveremos aplicando los siguientes pasos:
1ºIgualamos el polinomio del primer miembro
a cero y obtenemos las raíces de la ecuación de
segundo grado.
x2− 6x + 8 = 0

11. • En matemáticas, el valor absoluto o módulo1​ de un número real x, denotado por |x| es el valor de x sin considerar el signo,
sea este positivo o negativo​ Por ejemplo, el valor absoluto de 3 es 3 y el valor absoluto de −3 es 3 Algunos autores
extienden la noción de valor absoluto a los números complejos, donde el valor absoluto coincide con el módulo.
• El valor absoluto está vinculado con las nociones de magnitud, distancia y norma en diferentes contextos matemáticos y
físicos. El concepto de valor absoluto de un número real puede generalizarse a muchos otros objetos matemáticos, como
son los cuatermiones, anillos ordenados, cuerpos o espacios vectoriales
VALOR ABSOLUTO
DESIGUALDES DE VALOR ABSOLUTO
DESIGUALDADES DE VALOR ABSOLUTO (<)
Una desigualdad de valor absoluto es una
desigualdad que tiene un signo de valor absoluto
con una variable dentro.
La desigualdad significa que la distancia
entre x y 0 es menor que 4
Así, y El conjunto solución es
Cuando se resuelven desigualdades de valor
absoluto, hay dos casos a considerar.
Caso 1: La expresión dentro de los símbolos de valor
absoluto es positiva.
Caso 2: La expresión dentro de los símbolos de
valor absoluto es negativa.
La solución es la intersección de las soluciones de
estos dos casos.
En otras palabras, para cualesquiera números
reales y si entonces y
DESIGUALDADES DE VALOR ABSOLUTO (>)
La desigualdad significa que la distancia entre X y 0 es mayor
que 4
Así, o El conjunto solución es
Cuando se resuelven desigualdades de valor absoluto, hay dos casos a
considerar.
Caso 2: La expresión dentro de los símbolos de valor absoluto es
negativa.
En otras palabras, para cualesquiera números
reales y si entonces o
CONCLUSIÓN
Si el valor absoluto de la variable es menor que el término constante, entonces la gráfica resultante será
un segmento entre dos puntos. Si el valor absoluto de la variable es mayor que el término constante,
entonces la gráfica resultante consistirá en dos rayos apuntando al infinito en direcciones opuestas.

12. REFERENCIAS BIBLIOGRÁFICAS
www.Wikipedia.com
Material de apoyo para la unidad II/Moodle
http://localhost:8000/wiki/N%C3%BAmero_real
http://localhost:8000/wiki/Valor_absoluto

13. GRACIAS