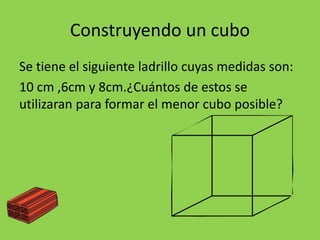
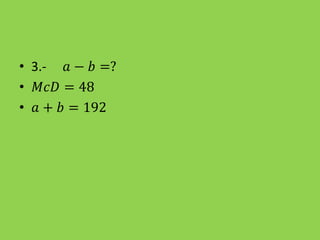El documento presenta diferentes métodos para calcular el máximo común divisor (MCD) y mínimo común múltiplo (MCM) de números. Explica cómo usar la descomposición, el algoritmo de Euclides y las propiedades de los MCD y MCM para resolver problemas que involucran estos conceptos.

1. Construyendo un cubo
Se tiene el siguiente ladrillo cuyas medidas son:
10 cm ,6cm y 8cm.¿Cuántos de estos se
utilizaran para formar el menor cubo posible?

2. Máximo común divisor y mínimo
común múltiplo
• Metodos para calcular el MCD
• Por descomposición simultanea.-
• 36 – 54 - 90 2
• 18 27 45 3 𝑀𝐶𝐷 36; 24; 90 =
• 6 9 15 3
• 2 3 5
• PESI

3. • Por descomposición canónica
• Ejemplo:
• 540 = 22
. 33
. 5
• 600 = 23
. 3. 52
→ 𝑀𝐶𝐷 540; 600; 450 =
• 450 = 2. 32
. 52

4. Por el algoritmo de Euclides o divisiones
sucesivas.-
ejemplo: hallar el MCD de 1037 y 850
división exacta
MCD(1037;850)=
cocientes 1 4 1 1 5
1037 850 187 102 17
residuos 187 102 0

5. MCM
• Metodos:
• Por descomposición canónica
• 4500 = 22
. 32
. 53
• 7425 = 33
. 52
. 11
• 1470 = 2.3.5. 72
• 𝑀𝐶𝑀 4500; 7425; 1470 =

6. • Por descomposición simultanea.-
• 60 – 90 – 150
𝑀𝐶𝑀 60; 90; 150 =

7. propiedades
1.- si A y B son PESÍ
𝑀𝐶𝐷 𝐴; 𝐵 = 1
𝑀𝐶𝑀 𝐴; 𝐵 = 𝐴. 𝐵
2.- si 𝐴 = 𝐵
𝑀𝐶𝐷 𝐴; 𝐵 = 𝐵
𝑀𝐶𝑀 𝐴; 𝐵 = 𝐴

8. 3.- si 𝑀𝐶𝐷 𝐴; 𝐵; 𝐶 = 𝑑 y
• 𝑀𝐶𝑀 𝐴; 𝐵; 𝐶 = 𝑚 , entonces:
•
𝐴
𝑑
= 𝑃1
•
𝐵
𝑑
= 𝑃2 PESÍ
•
𝐶
𝑑
= 𝑃3
•
𝑚
𝐴
= 𝐾1
•
𝑚
𝐵
= 𝐾2 PESÍ
•
𝑚
𝐶
= 𝐾3

9. 4.- para 2 números
𝑀𝐶𝐷 𝐴; 𝐵 𝑥𝑀𝐶𝑀 𝐴; 𝐵 = 𝐴𝑥𝐵
5.- si 𝑀𝐶𝐷 𝐴; 𝐵 = 𝑑 → 𝐴 = 𝑑𝑝 𝑦 𝐵 = 𝑑𝑞
𝑝 𝑦 𝑞 𝑠𝑜𝑛 𝑃𝐸𝑆Í , 𝑎𝑑𝑒𝑚𝑎𝑠, 𝑠𝑒 𝑐𝑢𝑚𝑝𝑙𝑒:
𝑀𝐶𝑀 𝐴; 𝐵 = 𝑑𝑝𝑞
6.- si 𝑀𝐶𝐷 𝐴; 𝐵; 𝐶 = 𝑑 𝑦 𝑀𝐶𝑀 𝐴; 𝐵; 𝐶 = 𝑚
𝑀𝐶𝐷 𝑘𝐴; 𝑘𝐵; 𝑘𝐶 = 𝑘𝑑
𝑀𝐶𝑀 𝑘𝐴; 𝑘𝐵; 𝑘𝐶 = 𝑘𝑚
𝑀𝐶𝐷
𝐴
𝑛
;
𝐵
𝑛
;
𝐶
𝑛
=
𝑑
𝑛
𝑀𝐶𝑀
𝐴
𝑛
;
𝐴
𝑛
;
𝐴
𝑛
=
𝑚
𝑛

10. Pagina 37
1.- 𝑥 =?
𝐴 = 12𝑥25 𝑥
𝐵 = 12 𝑥
. 225
𝑀𝐶𝑀 = 392 𝑑𝑖𝑣𝑖𝑠𝑜𝑟𝑒𝑠.
𝑥 ∈ 𝑧+

11. • 2.- 𝑀𝐶𝐷 𝑎; 𝑏 = 8
• 𝑀𝐶𝑀 =?
• 𝑎. 𝑏 = 4032

12. • 3.- 𝑎 − 𝑏 =?
• 𝑀𝑐𝐷 = 48
• 𝑎 + 𝑏 = 192

13. • 4.- 𝑀𝐶𝑀 𝑥; 𝑥 + 1 = 195
• 𝑥 + 𝑥 + 1 =

14. • 5.- en cuantos ceros termina el McD:
• 150150
; 160160
; 170170
; 180180

15. 6.- 𝑀𝐶𝐷 =?
33 … 334 y 77 … 778
462 cifras 378 cifras
Suma de cifras en base 16.

16. 7.- 𝑀𝑐𝐷 𝐴; 𝐵 =
𝑀𝑐𝐷 24𝐴; 64𝐵 = 720
𝑀𝐶𝐷 64𝐴; 24𝐵 = 480

17. 8.- 𝑎 =
𝑏 =
Datos:
𝑎 + 𝑏 = 224
𝑀𝑐𝐷 𝑎; 𝑏 = 56
resolución:

18. 9.- 𝑎 + 𝑏 =
𝑀𝑐𝐷 = 18
𝐷 𝑎 = 10
𝐷 𝑏=15

19. 10. Dos números A y tienen 16 múltiplos
comunes menores que 10000.sabiendo que el
McM de A y B tiene 18 divisores y que es
divisible entre 34,calcula (A+b),si se sabe que A
y B tiene 9 divisores comunes

20. 11. Se desea dividir tres barras de acero de
longitudes 165;225 y 345cm en trozos de igual
longitud ¿Cuál es el menor numero de trozos
que se pueden obtener?

21. 12. Mario sale con Ana cada 22 días ,con Betty
cada 45 días y con Claudia cada 15 días ,si sale
con las tres un lunes. Que día caerá cuando
vuelva a salir con las tres por cuarta vez?

22. 13.Si se cumple:
𝑀𝐶𝑀 𝑎 + 1; (𝑎 + 1)(𝑏 + 4)(𝑐 + 2) = 22344
Calcula: a+b+c

23. 14. Se compro un terreno , de forma rectangular,
cuyas dimensiones son 1620m y 3321m y lo
quieren dividir en parcelas cuadradas ,todas
iguales sin que sobre terreno ,y luego colocar
estas de tal modo que exista una estaca en cada
esquina de las parcelas. Calcula:
a. El menor numero de parcelas
b. El numero total de estacas
c. Da como respuesta A+B