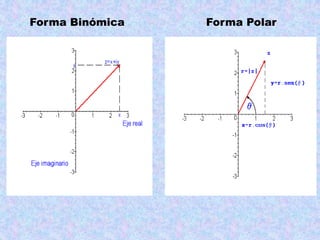
Los números complejos aparecieron inicialmente en el siglo XVI para resolver ecuaciones cuadráticas que tenían raíces cuadradas de números negativos. Fueron ignorados por mucho tiempo debido a su naturaleza extraña e imposible de representar. Finalmente, se establecieron formalmente los números complejos como pares ordenados de números reales para extender los números reales y poder representar todas las raíces de polinomios, convirtiéndose en una herramienta fundamental del álgebra.

1. Demetrio Ccesa Rayme

3. Una breve historia de estos números:
• Muchos conceptos en matemáticas tardaron varios años y hasta siglos en
desarrollarse, desde el momento en que fueron descubiertos por primera vez,
por alguna mente brillante, hasta la formalización de los mismos.
•El avance en el tiempo de la matemática fue un proceso lento, debido al
carácter formal de esta ciencia.
•Una de sus reglas es que cualquier objeto nuevo debe estar claramente
definido para ser aceptado por toda la comunidad.
•Los complejos aparecen inicialmente en el libro Ars magna de Girolamo
Cardano, publicado en 1545.
•Podemos decir que los números complejos aparecieron muy temprano en
el paisaje de las matemáticas, pero fueron ignorados sistemáticamente, por
su carácter extraño, carentes de sentido e imposibles de representar.
•Aparecen entre las soluciones de las ecuaciones cuadráticas, que generan
raíces cuadradas de números negativos.

4. •Por ejemplo, la ecuación
x2 + x + 5 = 0
•No posee soluciones reales. Si empleamos la conocida formula de resolución
de una ecuación de segundo grado, nos encontraremos con la raíz cuadrada de
19.
•Los matemáticos griegos, que conocían los métodos geométricos de
resolución, consideraban este tipo de problemas irresolubles.
•La razón por la que se crearon los números complejos es puramente
algebraica.
La ecuación: x*x + 1 = 0
no tiene solución para los números "normales" (Los que teóricamente
podemos construir en la realidad)
•Para resolver dicha ecuación hace falta un elemento que al multiplicarlo
por si mismo de menos 1 (el elemento neutro de la multiplicación).
Esto puede conseguirse con matrices, pero es un álgebra no conmutativa
y además hacen falta 4 elementos (matrices 2x2).
La solución más sencilla fue inventarse los Números Complejos.

6. Un número complejo Z es un par ordenado de números
reales X e Y, escrito como:
Z = (X,Y)
Dos números complejos son iguales
si solo sus partes reales e
imaginarias son iguales.
Son una extensión de
los números reales.
Los números
complejos representan
todas las raíces de
los polinomios.
Son la herramienta de
trabajo del álgebra
ordinaria.
Constituyen una de las
construcciones teóricas
más importantes de la
inteligencia humana.

8. Forma Binómica Forma Polar