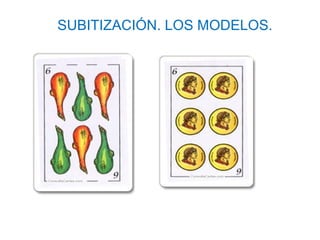
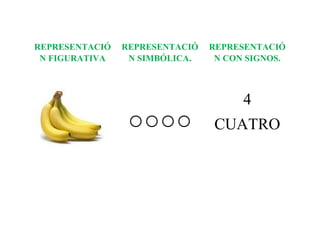
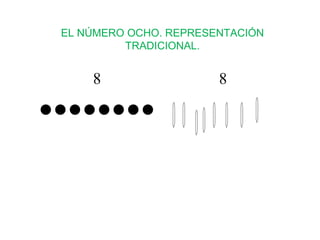
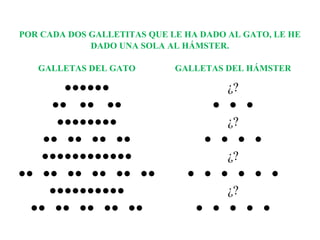
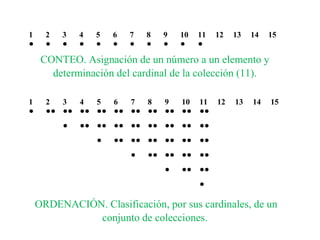
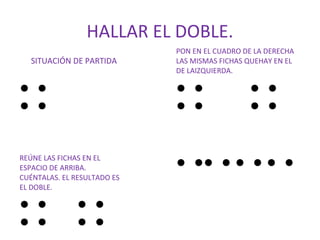
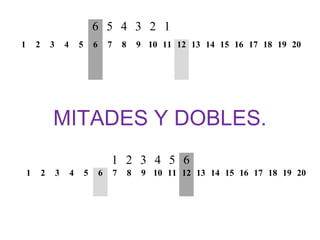
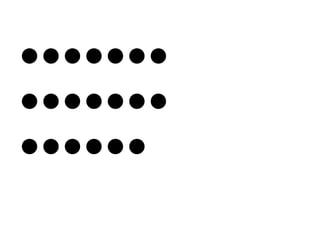El documento presenta los fundamentos del método ABN en educación infantil. Describe las bases del nuevo paradigma del aprendizaje numérico centrado en el desarrollo del sentido numérico. Explica conceptos como la subitización, la estimación, la estructura y representación de los números, y las transformaciones numéricas como la suma, resta, multiplicación y división a través de situaciones problema. El ponente es el Dr. Jaime Martínez Montero.