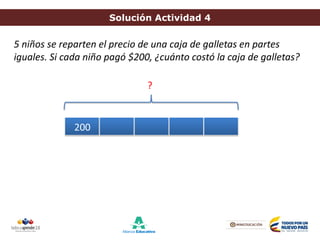
Este documento presenta el método del modelo de barras para enseñar conceptos matemáticos de manera concreta y visual. Explica que el modelo de barras usa dibujos para representar cantidades conocidas y desconocidas y sus relaciones en problemas. Propone actividades para que los estudiantes practiquen resolver problemas de adición, sustracción, multiplicación y división usando este método.

1. Pioneros Todos a Aprender

2. 1. Aplicación del Modelo de Barras

3. Objetivo general:
Mostrar cómo el método del modelo de barras permite
ilustrar los conceptos de las operaciones básicas y
resolver problemas empleando estas operaciones.
Objetivos específicos:
• Reconocer la importancia del uso de material
concreto y de representaciones pictóricas antes del
tratamiento abstracto de un problema.
• Plantear problemas relacionados con operaciones
básicas y que se puedan resolver con los modelos de
barras.
• Determinar diferentes variaciones de una situación
inicial, variando las incógnitas.
• Usar los modelos de barras en la solución de
problemas aritméticos básicos.
Objetivos

4. • Encargado de comunicar los resultados de su
equipo.
Vocero
• Controla el tiempo de las actividades y recoge
material necesario.
Relojero
• Se encarga de que todos participen y se respeten
los turnos.
Dinamizador
• Se encarga de tomar notas sobre las discusiones.Secretario
Distribución de grupos - roles

5. Método Singapur
CPA – Concreto – Pictórico - Abstracto
3 + 5 = 8
C P A
Manipula
objetos
Representa
objetos
Usa signos y
símbolos
matemáticos
Hacer Visualizar Simbolizar
Concreto Semi-concreto Abstracto

6. Trabajo en grupo
Discutir al interior de los grupos para
responder a las siguientes preguntas:
1. ¿En qué consiste el método del Modelo
de Barras?
2. ¿Qué ventajas tiene el Modelo de Barras?

7. Importancia del Modelo de Barras
El método propone a los
estudiantes hacer un dibujo o
modelo pictórico para
representar cantidades
conocidas y desconocidas y sus
relaciones en problemas con
cantidades.
Ayuda a los estudiantes,
especialmente a los más
visuales, a entender las cuatro
operaciones básicas (adición,
sustracción, multiplicación y
división) y resolver diferentes
problemas asociados con ellas.
Representar visualmente un problema
facilita su comprensión y por tanto permite
generar estrategias para una solución
acertada.
El modelo de barras es muy útil en la
aproximación concreta – pictórica –
abstracta que sigue el currículo de Singapur,
prepara a los estudiantes para la
manipulación simbólica en el álgebra y se
convierte también en una herramienta de la
misma.
Los estudiantes pueden usar objetos
concretos para dar sentido a conceptos de
Parte-Todo y de comparación.

8. El modelo de barras
• Es una estrategia de resolución de
problemas esencial para el enfoque
concreto - pictórico – abstracto.
• El modelo de barras es una
herramienta pictórica.
• Antes de llegar a la solución de un
problema, los estudiantes necesitan
comprenderlo y establecer relaciones
entre las cantidades conocidas y
desconocidas.
• El modelo permite visualizar y
establecer estas relaciones.
Modelo Parte-Todo
Modelo de Comparación

9. Actividad 1

10. Actividad 1
8 3
11

11. Actividad 1

12. Actividad 1
11
3 11

13. Actividad 2

14. Actividad 2 Solución
?
8 3
Juan tiene 8 peras y 3 mangos. ¿Cuántas frutas tiene Juan?

15. Actividad 2 Solución
11
8 3
Juan tiene 8 peras y 3 mangos. ¿Cuántas frutas tiene Juan?
Solución: Debemos sumar para hallar
la cantidad requerida.
Sumamos: 8 + 3 = 11
Respuesta: Juan tiene 11 frutas.

16. Actividad 2 Solución
11
8 3
Juan tiene 11 frutas. Tiene 8 peras y el resto son mangos.
¿Cuántos mangos tiene?
Solución: Debemos completar para
hallar la cantidad requerida.
Restamos: 11 - 8 = 3
Respuesta: Juan tiene 3 mangos.

17. Actividad 3
…

18. Actividad 3 Solución
Juan tiene 256 fichas y Beatriz tiene 134.
¿Cuántas fichas menos que Juan tiene Beatriz?
256Juan
Beatriz
?
134
…

19. Actividad 3 Solución
Juan tiene 256 fichas y Beatriz tiene 134.
¿Cuántas fichas menos que Juan tiene Beatriz?
256Juan
Beatriz
122
134
…
Solución: Debemos restar para
hallar la cantidad requerida.
Restamos: 256 – 134 = 122.
Respuesta: Beatriz tiene 122
fichas menos que Juan.

20. Actividad 3 Solución
b.) Juan tiene 256 fichas y Beatriz tiene 134.
¿Cuántas fichas tienen entre los dos?
256Juan
Beatriz
122
134
…
Solución: Debemos sumar para
hallar la cantidad requerida.
Sumamos: 256 + 134 = 390.
Respuesta: Beatriz y Juan tienen
390 fichas entre los dos.
390

21. Problema Actividad 3
En las últimas 5 temporadas Messi ha marcado 189 goles y James
ha marcado 42 menos que Messi.
¿Cuántos goles marcaron entre los dos?

22. Solución Problema Actividad 3
En las últimas 5 temporadas Messi ha marcado 189 goles y
James ha marcado 42 menos que Messi.
¿Cuántos goles marcaron entre los dos?
?
189Messi
James
42
?

23. ?
Solución Problema Actividad 3
En las últimas 5 temporadas Messi ha marcado 189 goles y
James ha marcado 42 menos que Messi.
¿Cuántos goles marcaron entre los dos?
189Messi
James
42
?
Solución: Primero debemos hallar cuántos goles ha marcado James.
Restamos: 189 – 42 = 147.
147
Ahora sumamos para hallar la cantidad que se pregunta:
189 + 147 = 336.
Respuesta: Messi y James marcaron 336 goles entre ambos.

24. Actividad 4
En grupos desarrollan la siguiente actividad:
Creen 6 problemas diferentes usando los
números 385, 523 y 138 que se puedan
solucionar utilizando el modelo de comparación
y resuélvalos

25. Actividad 4

26. Solución Actividad 4
?
5 niños se reparten el precio de una caja de galletas en partes
iguales. Si cada niño pagó $200, ¿cuánto costó la caja de galletas?
200

27. Solución Actividad 4
5 niños se reparten el precio de una caja de galletas en partes
iguales. Si cada niño pagó $200, ¿cuánto costó la caja de galletas?
1.000
200
Solución: debemos multiplicar para hallar la cantidad requerida:
5 x 200 = 1.000
Respuesta: La caja de galletas costó $1.000.
200 200 200 200

28. 1. María y José ahorran juntos $350.000. Si María ahorró $184.000. ¿Cuánto menos
que María ahorró José?
2. Santiago tiene 126 estampillas. Pablo tiene 83 estampillas más que Santiago.
¿Cuántas estampillas tienen en total?
3. La diferencia entre dos números es 15 el número mayor es 60. ¿Cuál es el número
menor?
4. En un mes 32.374 personas visitaron un museo de los cuales 21.254 eran niños.
• ¿Cuántos adultos visitaron el museo?
• ¿Cuántos niños más que adultos asistieron al museo?
5. En un centro comercial, la señora García gasta 4 veces más dinero que la señora Ortiz.
• ¿Cuánto gasta la señora Ortiz si la señora García gastó $98.000?
• ¿Cuánto más gastó la señora García que la señora Ortiz?
Problemas para practicar el modelo