Descargado 19 veces
Subido porDome Báez
Prueba Chi cuadradro χ²(1)
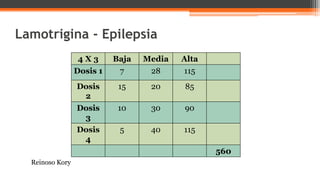
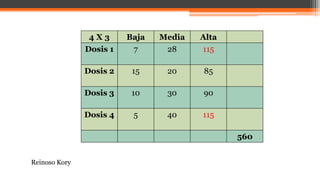
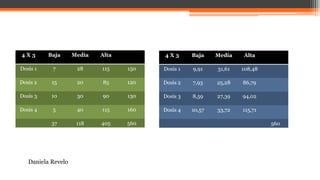
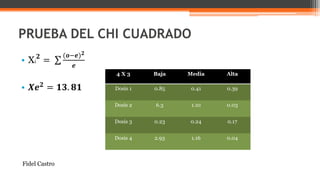
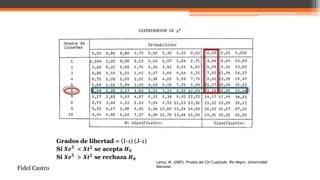
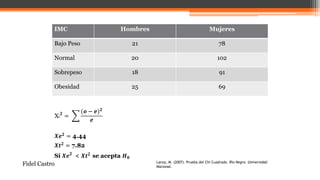
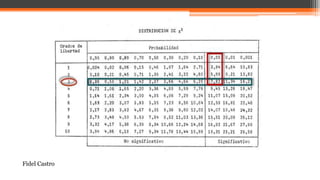
El documento explica la prueba de hipótesis chi cuadrado (χ2), que determina la relación entre dos variables cualitativas. Se intervienen conceptos como hipótesis nula y alternativa, frecuencias observadas y esperadas, y el método de comparación para validar la independencia de variables. Además, se presentan ejemplos prácticos que ilustran su aplicación en estudios de estado nutricional.
Más contenido relacionado
Similar a Prueba Chi cuadradro χ²(1)
Prueba Chi cuadradro χ²(1)
- 1. Prueba Xi² INTEGRANTES Báez Doménica CastroFidel Reinoso Kory Revelo Daniela
- 2. INTRODUCCIÓN Chi cuadrado (Xi²)es el nombre de una prueba de hipótesis que determina si dos variables están relacionadas o no.
- 3. ÍNDICE • Introducción • EstadísticaInferencial • Pruebas de Estimación • Prueba Xi² • Tabla de Contingencia • Hipótesis de Partida y Alternativa • Frecuencias Marginales • Tabla de χ² • Prueba de χ²
- 4. Estadística Inferencial • Sirvepara extrapolar, generalizar o estimar algo. PRUEBAS DE HIPÓTESIS - Hipótesis de trabajo - Hipótesis Nula Reinoso Kory
- 5. PRUEBAS DE ESTIMACIÓN Pruebaspara probar la hipótesis Reinoso Kory
- 6. Prueba Xi² Sirve paraestablecer una asociación entre dos variables cualitativas Reinoso Kory
- 7. Lamotrigina - Epilepsia 4X 3 Baja Media Alta Dosis 1 7 28 115 Dosis 2 15 20 85 Dosis 3 10 30 90 Dosis 4 5 40 115 560 Reinoso Kory
- 8. Hipótesis de Partida:H0.- Las dos variables en estudio son independientes Hipótesis Alternativa: H1.- Las dos variables en estudio están relacionadas o dependientes Reinoso Kory
- 9. 4 X 3Baja Media Alta Dosis 1 7 28 115 Dosis 2 15 20 85 Dosis 3 10 30 90 Dosis 4 5 40 115 560 Reinoso Kory
- 10. FRECUENCIAS MARGINALES FILA COLUMNA •f1= (7+28+115)= 150 f1= (7+15+10+5)= 37 • f2= (15+20+85)= 120 f2= (28+20+30+40)= 118 • f3= (10+30+90)= 130 f3= (115+85+90+115)= 405 • f4= (5+40+115)= 160 4 X 3 Baja Media Alta Dosis 1 7 28 115 Dosis 2 15 20 85 Dosis 3 10 30 90 Dosis 4 5 40 115 560 Reinoso Kory
- 11. 4 X 3Baja Media Alta Dosis 1 7 28 115 150 Dosis 2 15 20 85 120 Dosis 3 10 30 90 130 Dosis 4 5 40 115 160 37 118 405 560 Frecuencias Observadas Frecuencias Marginales (Fila /Columna) Gran Total - n Reinoso Kory
- 12. CONTRASTE DE LAHo 1. Calcular las frecuencias que se espera si las dos variables fueran independientes . 2. Calculamos la frecuencia esperada . 3. Comparamos los datos entre la frecuencia observada y la esperada. Daniela Revelo
- 13. Fe =(Total dela fila) (Total de la columna) / Total global Daniela Revelo
- 14. 4 X 3Baja Media Alta Dosis 1 7 28 115 150 Dosis 2 15 20 85 120 Dosis 3 10 30 90 130 Dosis 4 5 40 115 160 37 118 405 560 Fe =(Total de la fila) (Total de la columna) / Total global Fe =(150 x 37) / 560 = 9,91Daniela Revelo
- 15. fo11= 7 fe11=(150x37)/560=9,91 fo12=15 fe12=(120 x 37)/560 =7,93 fo13=10 fe13=(130x 37)/560 =8,59 fo14=5 fe14=(160 x 37)/560 =10,57 fo21=28 fe21=(150x118)/560 =31,61 fo31=115 fe31=(150x405)/560 =108,48 Daniela Revelo
- 16. 4 X 3Baja Media Alta Dosis 1 7 28 115 150 Dosis 2 15 20 85 120 Dosis 3 10 30 90 130 Dosis 4 5 40 115 160 37 118 405 560 4 X 3 Baja Media Alta Dosis 1 9,91 31,61 108,48 Dosis 2 7,93 25,28 86,79 Dosis 3 8,59 27,39 94,02 Dosis 4 10,57 33,72 115,71 560 Daniela Revelo
- 17. Cálculo de discrepancias •Estadígrafo de Contraste: • Xi²=∑ ( Fo ij- Feij)² / Fe ij • Fo ij: frecuencia observada • Fe ij : frecuencia esperada Si la hipótesis nula es cierta χ² sigue una distribución de Chi cuadrado con (I-1) (J-1) Rechazamos la H0 si cuando Xi² experimental > Xi² crítico
- 18. • Xi²=∑ (Fo ij- Feij)² / Fe ij • Xi²exp = (7-9.91)2/ 9.91 +….+ (115-115.71) 2 /115.71 = 13.87 Cálculo de discrepancias
- 19. • Xi²=∑ (Fo ij- Feij)² / Fe ij • Xi²exp = (7-9.91)2/ 9.91 +….+ (115-115.71) 2 /115.71 = 13.87 • Xi² 0.05, 6 • 13.87> 12.59 La respuesta depende del tratamiento Cálculo de discrepancias
- 20. PRUEBA DEL CHICUADRADO • Xi 𝟐 = (𝒐−𝒆) 𝟐 𝒆 • 𝑿𝒆 𝟐 = 𝟏𝟑. 𝟖𝟏 4 X 3 Baja Media Alta Dosis 1 0.85 0.41 0.39 Dosis 2 6.3 1.10 0.03 Dosis 3 0.23 0.24 0.17 Dosis 4 2.93 1.16 0.04 Fidel Castro
- 21.
- 23. Grados de libertad= (I-1) (J-1) Sí 𝑿𝒆 𝟐 < 𝑿𝒕 𝟐 se acepta 𝑯 𝟎 Sí 𝑿𝒆 𝟐 > 𝑿𝒕 𝟐 se rechaza 𝑯 𝟎 Lanza, M. (2007). Prueba del Chi Cuadrado. Río Negro. Universidad Nacional. Fidel Castro
- 24. • ¿Existen diferenciassignificativas en el estado nutricional entre hombres y mujeres? • 𝑯 𝟎: El estado nutricional es igual en hombres y mujeres. • 𝑯 𝒂: El estado nutricional de los hombres, NO es igual al de mujeres. Fidel Castro
- 25. IMC Hombres Mujeres BajoPeso 21 78 Normal 20 102 Sobrepeso 18 91 Obesidad 25 69 Xi 𝟐 = (𝒐 − 𝒆) 𝟐 𝒆 𝑿𝒆 𝟐 = 4.44 𝑿𝒕 𝟐 = 7.82 Sí 𝑿𝒆 𝟐 < 𝑿𝒕 𝟐 se acepta 𝑯 𝟎 Lanza, M. (2007). Prueba del Chi Cuadrado. Río Negro. Universidad Nacional. Fidel Castro
- 26. IMC Hombres Mujeres BajoPeso 19-64 79.38 Normal 24.16 97.83 Sobrepeso 21.59 87.40 Obesidad 18.62 75.37 Xi 𝟐 = (𝒐 − 𝒆) 𝟐 𝒆 𝑿𝒆 𝟐 = 4.44 𝑿𝒕 𝟐 = 7.82 Sí 𝑿𝒆 𝟐 < 𝑿𝒕 𝟐 se acepta 𝑯 𝟎 Lanza, M. (2007). Prueba del Chi Cuadrado. Río Negro. Universidad Nacional. Fidel Castro 𝑿𝒆 𝟐 = 0.09+0.71+0.59+2.18+0.02+0.17+0.14+0.53
- 27.
- 28. Bibliografía: • Lanza, M.(2007). Prueba del Chi Cuadrado. Río Negro. Universidad Nacional • Villardon, D. M. (20112). Estadística para Investigadores. Salamanca: PURD. • Martin Andres, L. d. (2010). Bioestadistica para las ciencias de la salud . España: Norma Capitel
- 29.