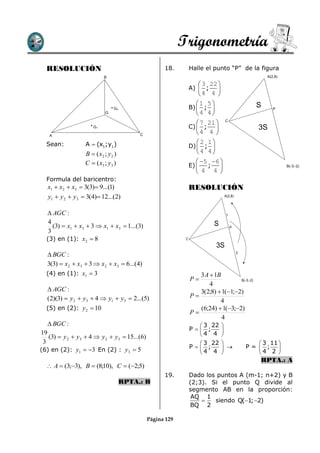
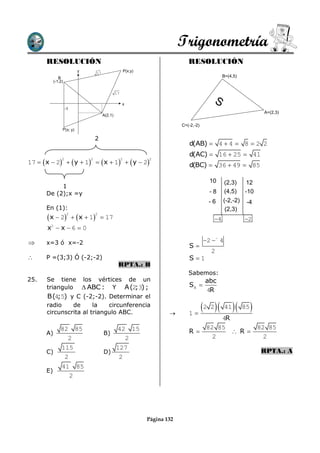
Este documento presenta 7 problemas de geometría analítica que involucran puntos, distancias, áreas y perímetros de figuras geométricas como cuadrados, triángulos y paralelogramos. Los problemas requieren calcular coordenadas, distancias, áreas y perímetros usando fórmulas trigonométricas y de geometría analítica.

1. Trigonometría
SEMANA 5 3. Los vértices de un cuadrado ABCD
GEOMETRÍA ANALÍTICA son: A(2;3) y C(5;7)
Halle el área del cuadrado.
1. Sean: A (-2;5); B (3;-2) y C
(10;b); puntos del plano. 5 15 25
A) B) C)
Si d (A, B) = d (B,C), Halle el 2 2 2
valor de b, si es negativo. 35 45
D) E)
2 2
A) -3 B) -5 C) -7
D) -8 E) -9
RESOLUCIÓN
C(5,7)
RERESOLUCIÓN
L
 2  3  5  2  3  10   2  b 
2 2 2 2
D B
2  b  5
donde: b=3  b  7
L
RPTA.:C A(2,3)
d  AC   5  2  7  3
2 2
2. Dado el punto A (-2;5) y B (m;8).
Halle la suma de valores de “m” si d  9  16
la distancia de AB es 5. d5
A) -1 B) -2 C) -3 Luego: L 2  5
D) -4 E) -6 2L2  25
25
L2 
RESOLUCIÓN 2
RPTA.: C
B(m;8)
4. Se tiene un triángulo equilátero
5
cuyos vértices son: A (-1;2) y
A(-2;5) B (2;6).
Determine el perímetro de dicho
triangulo.
m  2    8  5
2
d  AB    2
A) 20 B) 15 C) 10
m  2 
2
5 9 D) 11 E) 12
25  9  (m  2)2 RESOLUCIÓN
m  2
2
 16 B(2;6)
i) m  2  4m  2
ii) m  2  4  m  6 L
L
Suma = -4
A
RPTA.: D (-1;2)
L
C
Página 123

2. Trigonometría
6. Cuál de los siguientes triángulos
d  AB   2  1  6  2
2 2

ABC, tienen mayor área.
L  9  16
a) A (-5,0), B (1,2) y C (1,-2)
L 5 b) A (1,1), B (6-4) y C (5,3)
Luego: Perímetro=15 c) A (2,0) , B (6,0) y C (4,12)
RPTA.: B
A) a B) b
5. Tres vértices de un paralelogramo C) c D) Todos tiene igual área
son: A(-1;4), B( 1;-1) y C(6;1). Si
la ordenada del cuarto vértice “D”
RESOLUCIÓN
es “6”, Halle su abscisa.
5 0
A) 5 B) 4 C) 6 1 1 2 1
D) -4 E) -6
a)  10  2  10  2   122
2 1 2 2
5 0
RESOLUCIÓN
1 1
? 
y D  x;6  6 4 1
  b) 1  4  18  5  6  20  3  152
2 5 3 2
1 1
C(6;1)
A(-1;4) M 2 0
1 6 0 1
c)  72  24  242
x 2 4 12 2
0
2 0
B(1;-1)
RPTA.:C
En la figura:
AC 7. Encontrar las coordenadas de los
i) M  puntos que trisecan al segmento
2
AB , si: A  2;4 ,B(4;7)
BD
ii) M  Dar como respuesta el más
2
cercano a “B”
A C BD
 
2 2 A) 0;5 B) 0;5 C) 2;6
 A C BD
D)  2;5 E)  2; 6
 (-1;4)+(6;1)=(1;-1) +(X;6)
RESOLUCIÓN
 (4;6)=(X;6) B
P a (4;7)
a
 x 4
a
RPTA.: B A (-2;4)
Página 124

3. Trigonometría
A  2B RESOLUCIÓN
P
3
P
 2;4  2  4;7 A = 4S
3
P = (2; 6)
RPTA.: C
s
8. Se tiene el triángulo A (4,8),
B (6;-2), C (-10; 6). Halle la
distancia del vértice “B” al
baricentro del triángulo.
2 1
1 3 2 1
A) 2 6 B) 6 2 C) 5 3 S  4  9  1  3  3  6 
2 1  3 2
D) 6 6 E) 3 6
2 1
RESOLUCIÓN
1
B(6; -2) S= 14  S= 72
2
A = 4S
G
A = 28µ²
RPTA.: B
A(4; 8) C(-10; 6) 10. Se tiene un cuadrilátero cuyas
coordenadas son: A(-3;-1);
A BC B (-2,4); C (5;3) y D . Si M es el
G punto de intersección de sus
3 diagonales, halle la suma de las
G  0;4 coordenadas del punto N, si es
punto medio de CD . Donde:
BG  36  36 AM  MC;MD  2BM
BG  72  6 2 A) 3 B) 4 C) 5
D) 6 E) 7
RPTA.:B
9. Si los puntos medios de los lados
RESOLUCIÓN
de un triángulo son (2;1) , (3;-2) B(-2;4)
y (-1; -3). Calcule el área de dicho C(5;3)
triángulo. a
A) 142 B) 282 C) 182
D) 402 E) 202 M(1;1) N
2a
A( -3;1)
D(7;-5)
Página 125

4. Trigonometría
1  D  2(2;4)  23 4 
i) 1;1  =  ; 
12  3 3
Se pide:
D  (7; 5)
23 4
  9
(5;3)  (7; 5) 3 3
ii) N 
2 RPTA.: D
N  (6; 1) 12. Dos vértices de un triángulo
equilátero son (-2;9) y (3;-3).
Se pide: Cuánto mide la altura relativa a
dicho lado.
  6  (1)  5
RPTA.: C
A) 4, 5 3 B) 4, 5 3 C) 5, 5 3
11. Se tiene un triángulo ABC cuyas D) 5, 6 3 E) 6, 5 3
coordenadas de sus vértices son:
A (1;0), B (11;8) y C (x;0). Si M RESOLUCIÓN
es punto medio de AB y la
medida del ángulo agudo MCA es (-2;9)
  tg  0, 4 . Halle la suma de
60º d
las coordenadas del baricentro del
triángulo AMC. 13
A) 6 B) 7 C) 8 X 60º
D) 9 E) 10 30º
(3;-3)
13
RESOLUCIÓN
 2  3  9  3  13
2 2
y i) d 
B(11;8) Se pide:
x  6, 5 3
RPTA.: E
M(6;4)
13. El área de una región triángular es
2k S  42 , dos de sus vértices son
 x
A(1;0) C los puntos A (2;1) y B ( 3;-2); el
5k
tercer vértice C está situado en el
eje X. Halle sus coordenadas.
2
i) tg  0, 4 
5 1 
A)  ;0 ó (3;0)
ii) 2k  4  k  2 3 
1 
 C(16;0) B)  ;0 ó (5;0)
5 
iii) GAMC 
1;0  6;4  16;0  1 
3 C)   ;0 ó (5;0)
 3 
Página 126

5. Trigonometría
 1  A) 3;15 B) 4;16
D)   ;0 ó (3;0)
 5  C) 6;17 D) 7;18
 1 
E)   ;0 ó (5;0) E) 8;19
 5 
RESOLUCIÓN
RESOLUCIÓN
A(-1;2)
y
A(2;1) a
1
o x B(2;-5)
2 3
2a
2
B(3;-2)
C(x;y)
2a
r 2
3 -2 a
-2x x 0 0
Formula de división de un
0 2 1 x segmento en una razón dada:
3 3 -2
x  2  1
-4
3-2x X-4 2 x8
12
 x  4  3  2x  y  2 2
S4 5   y  19
2 12
 C  (8; 19)
 8 = 3x  7
RPTA.: E
i) 8 = 3x  7
15 = 3x 15. Los puntos medios de los lados de
x=5 un triángulo son P (2;5), Q (4;2)
ii) 8 = 3x  7 y R (1;1) . Halle las coordenadas
1 = 3x de los tres vértices.
1 Indique como respuesta la suma
x= 
3 de las abscisas y las ordenadas de
RPTA.:C los tres vértices.
14. El segmento que une A (1;2) con A) 7 B) 8 C) 10
D) 12 E) 15
B(2; 5) se prolonga hasta
C(x;y), sabiendo que
AC  3AB, Halle las coordenadas
de C.
Página 127

6. Trigonometría
RESOLUCIÓN A) (6;0) ó (1;0)
B) (3;0) ó (7;0)
P(2;5) B(x2;y2) C) (6;0) ó (-1;0)
C(x3;y3 ) D) (3;0) ó (8;0)
E) (-3;0) ó (1;0)
RESOLUCIÓN
R(1;1) Q(4;2)
M(2;2)
5
A(x1;y1 ) P(x;0)
Fórmula del Punto Medio: -2
N(5;-2)
x1  x2
4  x1  x2  8
2
x 2  x3 PM  x  22  2 2
2=  x 2  x3  4 (+)
2
PN  x  52  (2) 2
x 2  x3
1=  x1  x3  2
5  2
2
2 MN   (2  2)2
2x1  x2  x3   14
En todo se cumple:
 x1  x2  x3  7
PM   PN
2 2
 MN
2
y1  y 2
2=  y1  y 2  4 x  22  x  52  17
2
y  y3 x 2  7x  6  0
5= 2  y2  y3  10 (+)
2 x  6 ó x 1
y1  y3 RPTA.: A
1=  y1  y3  2
2
17. Si G (3; 4) es el baricentro de un
2 y1  y 2  y3   16 triángulo ABC y G,(4/3,2),
 y1  y 2  y3  8 G 2 (3;19/3) son los baricentros de
los triángulos formados uniendo G
 x1  x2  x3  y1  y 2  y3  15 con los vértices A, B y C;
determinar las coordenadas de
estos vértices.
RPTA.: E
A) (2;-2),(8;10),(-2;4)
16. Dado los puntos M (2;2) y B) (3;-3),(8;10),(-2;5)
N (5;-2). Determine en el eje de C) (1;-1),(8;10),(-2;5)
las abscisas un punto P de modo D) (3;-3),(6;8),(-1;4)
que el ángulo MPN sea recto. E) (3;-3),(6;8),(-1;4)
Página 128

7. Trigonometría
RESOLUCIÓN 18. Halle el punto “P” de la figura
B A(2,8)
 3 22 
A)  ; 
4 4 
1 5 S
G2 B)  ;  P
G 4 4
 7 21  C
G1 C)  ;  3S
A C 4 4 
Sean: A  (x1;y1 ) 2 1
D)  ; 
B  ( x2 ; y 2 ) 4 4
C  ( x3 ; y 3 )  5 6 
E)  ;  B(-3;-2)
 4 4 
Formula del baricentro:
x1  x2  x3  3(3) 9...(1) RESOLUCIÓN
y1  y 2  y3  3(4) 12...(2) A(2,8)
 AGC : 1
4 S
(3)  x1  x3  3  x1  x3  1...(3) P
3
(3) en (1): x2  8 C
3S
 BGC : 3
3(3)  x2  x3  3  x2  x3  6...(4)
(4) en (1): x1  3 3 A  1B
P B(-3;-2)
4
 AGC : 3(2;8)  1(1;2)
(2)(3)  y 2  y3  4  y1  y3  2...(5) P
4
(5) en (2): y 2  10 (6;24)  1(3;2)
P
4
 BGC :  3 22 
P ; 
19
(3)  y 2  y3  4  y 2  y3  15...(6) 4 4 
3  3 22   3 11 
(6) en (2): y1  3 En (2) : y3  5 P ;   P=  ; 
4 4  4 2 
RPTA.: A
 A  (3;3), B  (8;10), C  (2;5)
19. Dado los puntos A (m-1; n+2) y B
RPTA.: B (2;3). Si el punto Q divide al
segmento AB en la proporción:
AQ 1
 siendo Q(1; 2)
BQ 2
Página 129

8. Trigonometría
Halle: (m + n). RESOLUCIÓN
A) -2 B) -4 C) -6
D) -8 E) -10
RESOLUCIÓN
(2,3)
B
2
Q=(-1;-2)
1
Del gráfico:
A (m-1;n+2)
B  r. A
2 A  1B i) P
Q 1 r
3
3(1;  2)  2 A  (2; 3)  2;5  2 8,0
(3;  6)  2 A  (2; 3) x; y   3
2
(3;  6)  (2; 3)  2 A 1
3
2 A  (5;  9)
x; y   2;3
2(m  1; n  2)  (5;  9)
2m  2; 2n  4   5;  9 ii) PQ  7  2   15  3
2 2
3  PQ  13
2m  2  5  2m  3  m  RPTA.: A
2
3
2m  4  9  2n  13  m  21. Halle el área de aquella región
2 triángular donde 2 de sus vértices
m  n  -8 son (0;0) y (6;6), además se sabe
que el punto de intersección de
RPTA.: D sus medianas es ( 4/3 ;4).
20. En la figura, calcule la distancia
A) 32 B) 62 C) 242
PQ, Si S: Área
A(8;0)
D) 122 E) 482
3S RESOLUCIÓN
y
2S P
C (x;y)
B(6;6)
B(-2;-5)
A) 13 B) 12
Q(7;-15)
C) 5
S G(
4
3
;3)
D) 24 E) 26
A(0;0) x
Página 130

9. Trigonometría
Del Gráfico:
A BC 23. Si 0 (0;0); A 12;a  IC y
i) G B(6;0) , donde P(4;3) es el punto
3
de intersección de OA y BC . Si P
 4  0;0  6;6  x; y 
 ; 3  divide a ambos segmentos en la
3  3 misma razón. Halle la suma de las
 x; y    2; 6 coordenadas del punto

C CP  PB . 
A 00
1 B 1 66 A) 6 B) 7 C) 8
ii) S= 
2 C 2  26 D) 9 E) 10
D 00
RESOLUCIÓN
S=
1
48  24 2 y A(12;a)
2
C 6
10
RPTA.: C 2k
8
22. Los puntos A(-2;3); B(1;1), 5 P(4;3)
C(3;a) con a >0 y D(b;c) son los 3 k 3
vértices de un cuadrado. B(6;0)
x
0
Calcule: V  a  b  c 4 8
A) 6 B) 10 C) 8
D) 2 E) 12 1  C  2 6;0
i) 4;3 
12
RESOLUCIÓN
 C  0;9
y
Se pide:
D
   09  9
 RPTA.: D
C
A(-2;3)  24. El lado desigual de un triángulo
 isósceles tiene por extremos los
  puntos A (2;-1) y B (-1;2) y los
B(1;1) lados iguales miden cada uno
o x
17u ., Halle el vértice opuesto al
de donde : lado desigual.
C (3; a)  C (3;4)
D(b; c)  D(0;6) A) (1;1) ó (-3;-3)
Se pide: B) (3;3) ó (-2;-2)
V  abc C) (4;4) ó (-1;1)
D) (5;5) ó (-2;2)
V  406
E) (-3,3) ó (3;3)
V  10
RPTA.:B
Página 131

10. Trigonometría
RESOLUCIÓN RESOLUCIÓN
y P(x;y)
17
B B=(4,5)
(-1;2)
17
x
S
-1
A=(2,3)
A(2,1)
C=(-2,-2)
P(x; y)
2
d(AB)  4  4  8  2 2
d(AC)  16  25  41
17   x  2   y  1   x  1   y  2
2 2 2 2
d(BC)  36  49  85
10 (2,3) 12
1
De (2);x =y -8 (4,5) -10
-6 (-2,-2) -4
En (1): (2,3)
 x  2   x  1  17
2 2
4 2
x  x 6  0
2
 x=3 ó x=-2 2  4
S
2
 P =(3;3) Ó (-2;-2) S1
RPTA.: B
Sabemos:
25. Se tiene los vértices de un abc
triangulo  ABC : Y A (2 3) ;
; S 
4R
B(4;5) y C (-2;-2). Determinar el
radio de la circunferencia
circunscrita al triangulo ABC.  1
2 2 41  85 
4R
82 85 42 15 82 85 82 85
A) B) R  R
2 2 2 2
115 127
C) D) RPTA.: A
2 2
41 85
E)
2
Página 132