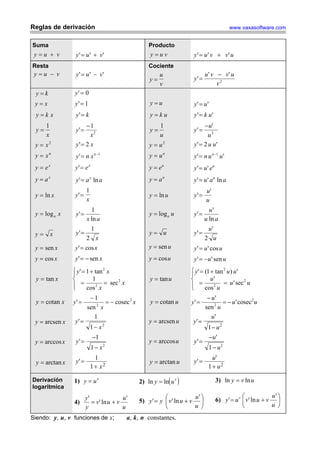
Este documento proporciona reglas para derivar funciones comunes. Incluye reglas para la suma, resta, producto y cociente de funciones, así como funciones exponenciales, logarítmicas y trigonométricas. También presenta tres métodos para derivar funciones logarítmicas.

1. Reglas de derivación www.vaxasoftware.com
Suma Producto
y=u + v y ' = u ' + v' y=uv y ' = u ' v + v' u
Resta Cociente
y=u − v y ' = u ' − v' u u ' v − v' u
y= y' =
v v2
y=k y' = 0
y=x y' = 1 y=u y' = u'
y=k x y' = k y=ku y' = k u'
1 −1 1 − u'
y= y' = y= y' =
x x2 u u2
y = x2 y' = 2 x y = u2 y' = 2 u u'
y = xn y ' = n x n −1 y = un y ' = n u n−1 u '
y = ex y' = e x y = eu y '= u ' eu
y = ax y '= a x ln a y = au y '= u ' a u ln a
1 u'
y = ln x y' = y = ln u y' =
x u
1 u'
y = log a x y '= y = log a u y '=
x ln a u ln a
1 u'
y= x y '= y= u y '=
2 x 2 u
y = sen x y ' = cos x y = sen u y ' = u ' cos u
y = cos x y ' = − sen x y = cos u y ' = −u ' sen u
⎧ y ' = 1 + tan 2 x ⎧ y ' = (1 + tan 2 u ) u '
⎪ ⎪
y = tan x ⎨ 1 y = tan u ⎨ u'
⎪ = cos 2 x = sec x ⎪ = cos 2 u = u ' sec u
2 2
⎩ ⎩
−1 − u'
y = cotan x y' = 2
= − cosec 2 x y = cotan u y' = 2
= − u ' cosec 2u
sen x sen u
1 u'
y = arcsen x y' = y = arcsen u y' =
1− x2 1 − u2
−1 −u'
y = arccos x y' = y = arccos u y' =
1 − x2 1 − u2
1 u'
y = arctan x y' = y = arctan u y' =
1+ x2 1 + u2
Derivación 1) y = u v 2) ln y = ln( u v ) 3) ln y = v ln u
logarítmica
⎛ u' ⎞ ⎛ u' ⎞
4)
y'
= v' ln u + v
u' 5) y ' = y ⎜ v' ln u + v ⎟ 6) y ' = u v ⎜ v' ln u + v ⎟
y u ⎝ u ⎠ ⎝ u ⎠
Siendo: y, u, v funciones de x; a, k, n constantes.