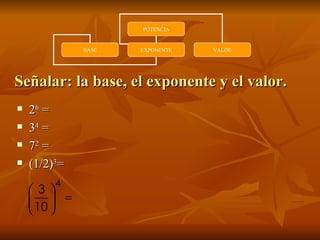
Este documento explica los conceptos básicos de las potencias. Define potencia como un producto de factores iguales. Presenta las propiedades de las potencias como la multiplicación, división, potencias de exponente cero y negativo. También cubre cómo calcular potencias de potencias y el producto y división de potencias de igual exponente. Finalmente, introduce la notación científica para escribir números muy grandes y pequeños usando potencias de 10.

1. POTENCIAS a n = a·a·a·a·……(n veces a) Concepto: Potencia es un Producto de factores iguales

2. 2 6 = 3 4 = 7 2 = (1/2) 3 = Señalar: la base, el exponente y el valor. POTENCIA BASE EXPONENTE VALOR

3. Ley de los signos Potencia de exponente Par(2n), tiene signo…. (+b) 2n = positivo, si base es positiva (-b) 2n = positivo, si la base es negativa Potencia de exponente Impar(2n+1), tiene signo….. (+b) 2n+1 = positivo, si la base es positiva (-b) 2n+1 = negativo, si la base es negativa

4. Responder, si el signo será + ó - (-2) 4 = (-3) 2 = (-10) 5 = (-5) 3 = (+7) 3 =

5. Propiedades de las potencias Multiplicación de Potencia de igual base: 2 3 · 2 4 = 6 2 · 6 -4 · 6 · 6 3 = División de Potencias de igual base: 7 5 : 7 3 = ( 5 7 : 5 ) : 5 4 = En símbolos: a n : a m = a n - m Se deja la base y se restan los exponentes En símbolos: a n · a m = a n + m Se deja la base y se suman los exponentes

6. Potencia de Exponente Cero 7 3 : 7 3 = 7 3-3 = 7 0 = 1 Toda Potencia de exponente cero es igual a…. Responder (-9) 0 = 15 0 = -6 0 = En símbolos : B 0 = 1 La potencia de exponente cero siempre es igual a 1

7. Potencia de Exponente Negativo 10 3 : 10 5 = 10 3 - 5 = 10 -2 Luego: Responder: 3 -3 7 -2 En símbolos: B -n = 1 / b n Se calcula la potencia y luego se invierte su valor.

8. Potencia de una Potencia (10 3 ) 2 = 10 3 · 10 3 = 10 6 (10 3 ) 2 = 10 3·2 = 10 6 Responder. ( 2 4 ) 2 = ( 5 4 ) 3 = ( 0,3 5 ) 2 = En símbolos: (B n ) m = B n · m Se deja la base y se multiplican los exponentes.

9. Producto de Potencias de igual exponente 5 4 · 2 4 = 5·5·5·5·2·2·2·2 Asociando (5·2) (5·2) (5·2) (5·2) 10·10·10·10 = 10 4 Luego: 5 4 · 2 4 = 10 4 Ejercicios. 3 5 · 8 5 = 5 6 · 2 6 = (-4) 3 · 6 3 = En símbolos: a n · b n = (a · b) n Se multiplican las bases y se deja el exponente

10. División de Potencias de igual exponente 6 4 : 3 4 =(6 : 3) 4 = 2 4 15 3 : 5 3 =(15 : 5) 3 = 3 3 Responder. 10 6 : 5 6 = 21 4 : 7 4 = (-20) 3 : (4) 3 = En símbolos: a n : b n =(a : b) n Se dividen las bases y se deja el exponente.

11. Problemas: ¿Cuál es el área de un terreno de forma rectangular de 5 3 metros de largo y 2 3 de ancho? ¿Cuál es área de una habitación cuadrada cuyos lados mide 2 4 metros? ¿Cuál será la medida de ancho de un rectángulo, si su área es 10 4 cm 2 y el largo mide 5 4 cm?

12. Notación Científica Para escribir cantidades muy grandes: 18.000.000 = 235.000.000 = Para escribir cantidades pequeñas: 0,00005 = 0,00000457 = Conclusión : Escribir en notación científica es utilizar un producto de un número por una potencia de 10. En símbolos: k ·10 n tal que: n es un número entero 1 <= k < 10

13. Trabajo individual de profundización Desarrollar las guías de potencias. Hacerla en forma ordenada en el cuaderno. Resolver los ejercicios del librito. Consultar aquellos problemas o ejercicios en que tenga dudas.