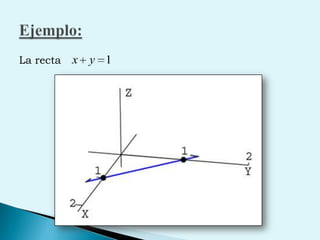
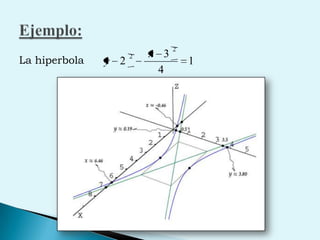
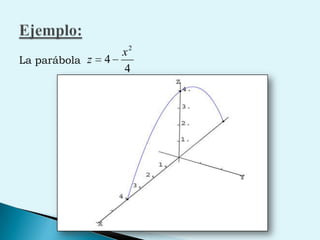
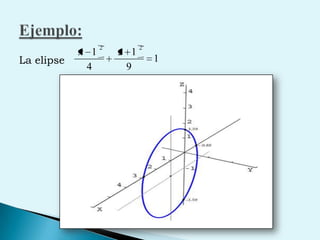
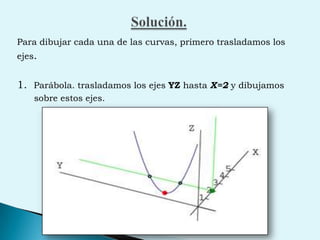
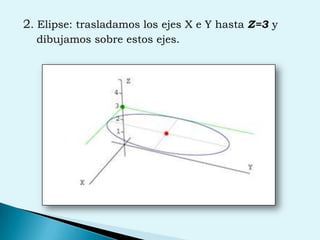
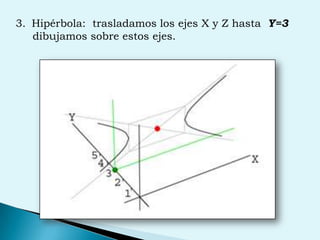
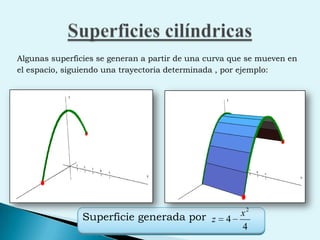
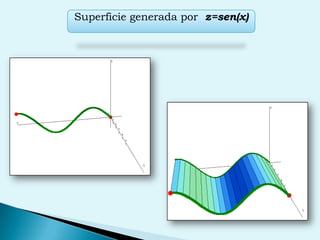
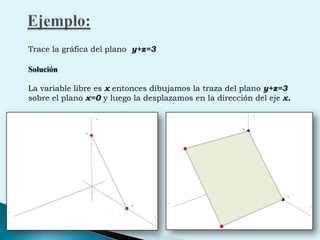
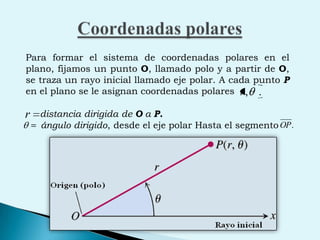
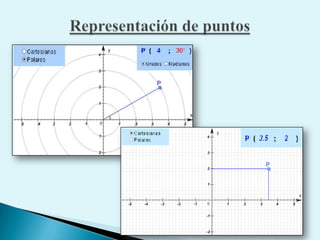
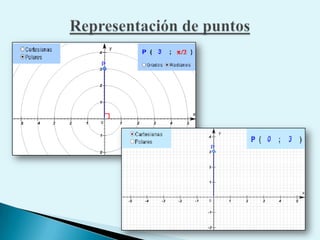
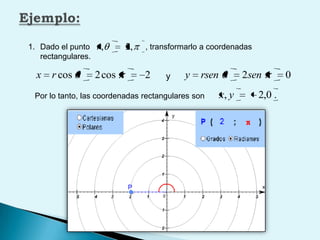
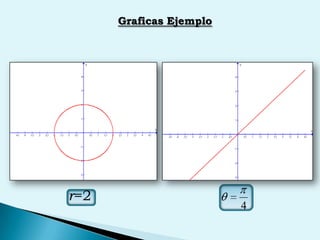
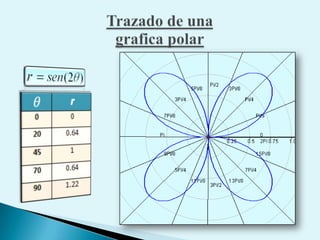
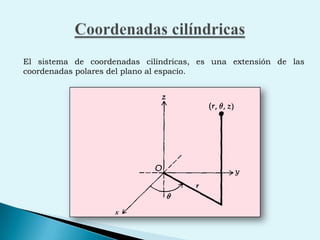
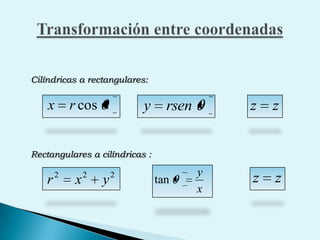
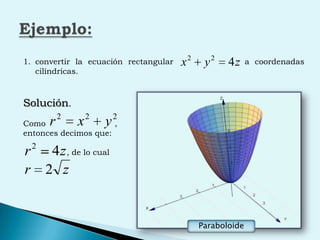
El documento describe conceptos clave de cálculo como superficies, vectores, derivadas parciales y curvas en el espacio. Explica cómo representar curvas en diferentes planos y como generar superficies cilíndricas y de revolución. También introduce coordenadas polares, cilíndricas y cómo transformar entre diferentes sistemas de coordenadas. Finalmente, presenta ejemplos de ecuaciones de superficies como la esfera, el paraboloide y el hiperboloide.

1. SUPERFICIESMódulo 4

2. ¿Cómo puedo aplicar comprensivamente el cálculo en mi carrera?Tópico generativo

3. Los estudiantes apreciaran como el concepto de superficie es clave para la comprensión del cálculo.Hilo conductor

4. Los alumnos comprenderán:Los vectores en el plano y en el espacio representándolos geométricamente en diversas situaciones que ocurren en su entorno aplicándolos en los cursos vistos durante el semestre y en la solución de diversos problemas propios del cálculo y de otras materias.Los conceptos de derivadas parciales y direccionales como una generalización del concepto de derivada, aplicándolos a la solución de diversos problemas propios del cálculo y de otras materias.Integrales múltiples y de línea, a través de aplicaciones relacionadas con el entorno, aplicándolos a la solución de diversos problemas propios del cálculo y de otras materias.Metas de comprensión

5. CURVAS EN EL ESPACIOConsideremos curvas en plano tridimensional, pero definidas sobre uno de los planos XY, XZ o YZ y con ecuaciones del tipo:En el plano XY F(x,y)=0En el plano XZ F(x,z)=0En el plano YZ F(y,z)=0

6. La recta Ejemplo:

7. La hiperbola Ejemplo:

8. La parábola Ejemplo:

9. La elipse Ejemplo:

10. Una curva sobre un plano x=a , y=b o z=c, se describe dando la ecuación de la curva y el plano sobre la cual se encuentra.Ejemplo: Dibujar las curvas:1. Parábola , sobre el plano x=2.2. Elipse , sobre el plano z=3.3. Hipérbola , sobre el plano y=3.Curvas sobre los planos

11. Solución.Para dibujar cada una de las curvas, primero trasladamos los ejes. 1. Parábola. trasladamos los ejes YZ hasta X=2 y dibujamos sobre estos ejes.

12. 2. Elipse: trasladamos los ejes X e Y hasta Z=3 y dibujamos sobre estos ejes.

13. Hipérbola: trasladamos los ejes X y Z hasta Y=3 dibujamos sobre estos ejes.

14. Algunas superficies se generan a partir de una curva que se mueven en el espacio, siguiendo una trayectoria determinada , por ejemplo:Superficie generada porSuperficies cilíndricas

15. Superficie generada por z=sen(x)

16. Variable libreSi en la ecuación F(x,y,z)=0 algunas de las variables X,Y o z es libre (no aparece en la ecuación), entonces su gráfica corresponde a un cilindro y trazarla resulta muy simple : primero dibujamos la traza de la superficie F(x,y,z)=0 sobre el plano coordenado correspondiente a las variables no libres y luego movemos esta curva en la dirección del eje coordenado correspondiente a la variable libre.

17. Ejemplo:Trazar la gráfica de la superficie cilíndricaSoluciónLa variable libre es z entonces dibujamos la traza sobre el plano z=0 (plano xy) y la desplazamos a lo largo del eje z.

18. Ejemplo:Trace la gráfica del plano y+z=3SoluciónLa variable libre es x entonces dibujamos la traza del plano y+z=3sobre el plano x=0 y luego la desplazamos en la dirección del eje x.

19. Ejercicios:Trazar la gráfica de la superficie cilíndrica.

20. Coordenadas polaresPara formar el sistema de coordenadas polares en el plano, fijamos un punto O, llamado polo y a partir de O, se traza un rayo inicial llamado eje polar. A cada punto P en el plano se le asignan coordenadas polares distancia dirigida de O a P.ángulo dirigido, desde el eje polar Hasta el segmento

21. Representación de puntos

22. Representación de puntos

23. Las coordenadas polares de un punto están relacionadas con las coordenadas rectangulares de ese punto como se muestra a continuación .Transformación de coordenadas

24. Ejemplo:Dado el punto , transformarlo a coordenadas rectangulares.y Por lo tanto, las coordenadas rectangulares son

25. Ejemplo:Dado el punto , transformarlo a coordenadas polares. además,Ahora como se eligió en el mismo cuadrante que entonces

26. Ejercicios:Dado el punto , transformarlo a coordenadas rectangulares.Dado el punto , transformarlo a coordenadas polares.

27. Gráficas polaresEjemplo:Describir la grafica de las siguientes ecuaciones polares:r=2Solución.Sabemos que , por lo tanto tenemos que Utilicemos la relación , de lo cual obtenemos:

28. Graficas Ejemplor=2

29. Trazado de una grafica polar

30. Coordenadas cilíndricasEl sistema de coordenadas cilíndricas, es una extensión de las coordenadas polares del plano al espacio.

31. Cilíndricas a rectangulares:Rectangulares a cilíndricas :Transformación entre coordenadas

32. Ejemplo:convertir la ecuación rectangular a coordenadas cilíndricas. Solución.Como ,entonces decimos que: , de lo cual Paraboloide

33. Ejemplo:convertir la ecuación cilíndrica a coordenadas rectangulares. Solución. ,Hiperboloide de dos hojas

34. Ejemplo:Hallar una ecuación en coordenadas cilíndricas para la ecuación Solución. ,Esfera

35. Ejercicios:Hallar una ecuación en coordenadas cilíndricas para:

36. bibliografíaIngresar palabras claves en diferentes buscadores tales como: Applet coordenadas polares.