El documento presenta información sobre las ecuaciones y elementos de las secciones cónicas (círculo, elipse, parábola e hipérbola), incluyendo sus ecuaciones generales, centros, radios, focos, vértices y asíntotas. También incluye ejercicios resueltos sobre cómo encontrar dichos elementos y realizar operaciones geométricas con estas curvas como determinar puntos de intersección y graficar ecuaciones.

1. TALLERES SOBRE SECCIONES
CÓNICAS

2. Círculo Elipse Parábola Hipérbola
Ecuación (vértice
horizontal):
x2 + y2 = r2 x2 / a2 + y2 / b2 = 1 4px = y2 x2 / a2 - y2 / b2 = 1
Ecuaciones de las asíntotas: y = ± (b/a)x
Ecuación (vértice vertical): x2 + y2 = r2 y2 / a2 + x2 / b2 = 1 4py = x2 y2 / a2 - x2 / b2 = 1
Ecuaciones de las asíntotas: x = ± (b/a)y
Variables: r = el radio del círculo
a = el radio mayor (= 1/2 la
longitud del eje mayor)
b = el radio menor (= 1/2 la
longitud del eje menor)
c = la distancia desde el
centre al foco
p = la distancia desde el
vértice al foco (o a la
directriz)
a = 1/2 la longitud del eje
mayor
b = 1/2 la longitud del eje
menor
c = la distancia desde el
centro al foco
Excentricidad: 0 c/a c/a
El Relación al Foco: p = 0 a2 - b2 = c2 p = p a2 + b2 = c2
Definición: es el conjunto
de todos los puntos que
cumple la condición...
la distancia al origen es
constante
la suma del las distancias a
cada foco es constante
la distancia al foco = la
distancia a la directriz
la diferencia entre las
distancias a cada foco es
constante

3. Taller sobre circunferencia
1. Determina el radio de las siguientes circunferencias:
• a) x2 + y2= 16
• b) x2 + y2 = 12
• c) 9x2+ 9y2= 4
• d) 5x2 + 5y2 = 8
2. Escribe la ecuación de la circunferencia que tiene su centro en el origen y cuyo radio mide:
• a) 6 cm.
• b) 3.5cm.
• d) 10 cm.
3. Escribe la ecuación de la circunferencia:
• a) de centro C(6, -4) y radio 5 unidades
• b) de centro C(-1, -5) y radio 2/3

4. 4. Determina el centro y el radio de las siguientes circunferencias:
• a) (x - 5)2 + (y - 1)2 = 4
• b) (x + 2/5)2 + (y - 3/4)2= 3
• c) x2 + y2 - 2x + 16y -14 = 0
• d) 2x2 + 8x + 2y2 - 6y = 18.
• e) [5(x + 4)]2 + 25(y - 2)2 = 625
5. Escribe en forma canónica la ecuación de la circunferencia
• x2 + y2 + 4x -10y + 11 = 0
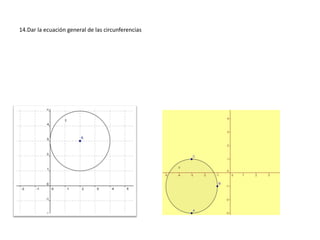
6. Grafica las circunferencias que tienen las ecuaciones:
• a) x2 + y2 = 4.
• b) (x - 5)2 + (y - 1)2 = 4

5. 7. Encuentra la ecuación de la circunferencia que pasa por los puntos
• a) (3,0); (-1,6); (-2,-4).
• b) (1,-4); (4,5); (3,-2).
8. Determina la ecuación de la circunferencia que pasa por los puntos (-2,4) y (3,6), y cuyo centro
está sobre la recta de ecuación 2x + y = 3.
9. Determina los puntos de intersección de las circunferencias
• X2 + y2 = 25 y
• X2 + y2+x + y - 20 = 0.

6. 10. Determina en qué puntos son secantes las circunferencias
• (x - 3)2 + (y - 2)2 = 16 y
• (x - 7)2 + (y - 2)2 = 16
11. Encuentra la ecuación de la recta que pasa por los puntos de intersección de las circunferencias
• X2 + y2 - 4x + 2y - 4 = 0 y
• X2 + y2 + 4x = 0
12. Calcula la distancia entre los centros de las circunferencias
• X2 + y2 - 6x -2y - 6 = 0 y
• X2 + y2 - 12x + 4y + 31 = 0
13. La ecuación de una circunferencia es x2 + y2 = 50. El punto medio de una cuerda de esta
circunferencia es el punto (-2, 4). Hallar la ecuación de la cuerda.
•

7. 14.Dar la ecuación general de las circunferencias

8. Taller sobre parábola
1. Usando la definición, hallar la ecuación de la parábola que tiene su foco en F(2,0) y su
dirección DD es la recta de ecuación x = -2 trazar la gráfica.
• 2. Dada la parábola que tiene por ecuación x2 = -6y, encontrar las coordenadas del
foco, la ecuación de la directriz, analizar la simetría de la curva y trazar la gráfica.
• 3. Determine el vértice V y la ecuación de la parábola que tiene como directriz la recta de
ecuación x = 2 y cuyo foco está localizado en el punto F(4, 2) y trazar la gráfica.

9. 4. Determine el vértice V, el foco F, la ecuación de la directriz, el eje focal y dibujar la gráfica
de la parábola cuya ecuación es:
• 6y2 + 16x - 8y + 14 = 0
5. Determinar los elementos de la parábola y dibujar la gráfica:
• X2 - 6x - 6y + 39 = 0

10. 6. Dar la ecuación general de las parábolas

11. Taller sobre elipse
1. Determinar los elementos de las elipses escribir las ecuaciones canónicas y dibujarlas
• 8x2 + 3y2 = 12
• 3x2 + 2y2 = 48
• 2y2 + 11x2 + 36y + 44x + 184 = 0.
• 30y2+ 32x2 - 120y - 64x - 808 = 0
2. Hallar la ecuación general de las elipses que cumplan las condiciones dadas y dibujarlas.
• Centro en (0,0), foco (-3,0), vértice (5,0)
• Vértices en (4,3) y (4,9) foco en el punto (4,8).
• Focos en (5,1) y (-1,1). Longitud del eje mayor 8.
• Centro en (-3,1), foco en (-3,0). Vértice en (-3,3).
• Centro en (-2,9), focos en (-4,9) (0,9). Longitud del eje menor 4.

12. 3. Dar la ecuación general de las elipses

13. Taller de hipérbola
1. Dar las ecuaciones generales y graficar las hipérbolas que cumplen las condiciones dadas:
• Centro en (4,-1), foco (7,-1), vértice (6,-1)
• Foco (-1,0), vértices (-4,4) y (-4,2).
• Focos (3,7) y (7,7), vértice (6,7)
• Foco (-1,0), vértices (-4,4) y (-4,2).

14. 2. Encontrar los elementos y graficar las hipérbolas que tienen las siguientes ecuaciones:
• 9x2- 16y2 = 144
• 25y2 - 10x2 = 250
• (x+1)2- (y+2)2= 4
• 4x2 - 25y2 - 8x - 100y - 196 = 0
• x2 - 4y2 + 6x + 24y - 40 = 0

15. 3. Dar la ecuación general de las hipérbolas

16. Taller sobre todas las secciones cónicas
1. Hallar la ecuación de la circunferencia centrada en el punto (5, -2) y de radio 3.
2. Hallar el centro y el radio de la circunferencia cuya ecuación es
• X2+ y2 - 4x + 6y + 3=0
3. Reducir la ecuación 4x2 + 9y2 - 8x + 18y - 23 = 0. Si se trata de una elipse, hallar su centro, sus
focos y sus vértices.
4. Hallar los elementos de la elipse
• 25x2 + 16y2- 50x + 64y - 311 = 0

17. 5. Hallar la ecuación reducida de la hipérbola
• 4x2 - 9y2 - 8x + 36y + 4 = 0. Hallar su centro, sus vértices, sus focos y sus asíntotas.
6.Reducir la ecuación 4x2 + 9y2 - 8x + 18y - 23 = 0. Si se trata de una elipse, hallar su centro,
sus focos y sus vértices.
7. Hallar los elementos de la elipse
• 25x2 + 16y2- 50x + 64y - 311 = 0
8. Hallar la ecuación reducida de la hipérbola
• 4x2 - 9y2 - 8x + 36y + 4 = 0. Hallar su centro, sus vértices, sus focos y sus asíntotas.

18. 9. Hallar la ecuación reducida de la parábola
• 2x2 + 8x + 3y - 5 = 0.
10.Hallar su vértice, su foco y su directriz.
• X2+6x-2y-1=0
• (x+3)=(y+2)2
• 8(y+1)=(x-1)2
11. Hallar los puntos de intersección de la recta x + y + 1 = 0 y la elipse
• 2x2 + 3y2 - 4x + 6y - 9 = 0.