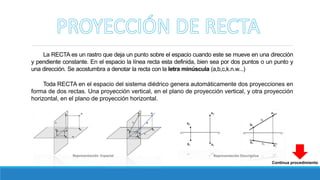
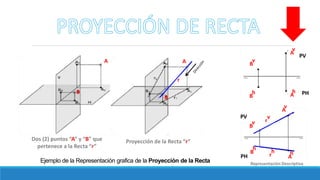
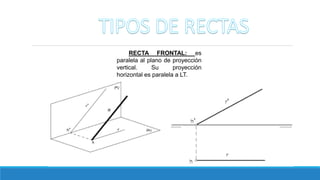
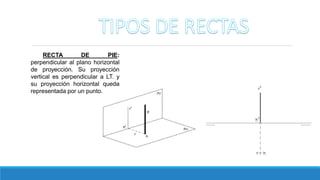
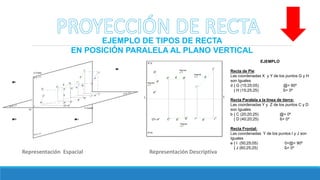
El documento resume los diferentes tipos de rectas en el sistema de representación descriptiva, incluyendo rectas horizontales, frontales, de punta, de pie, paralelas a la línea de tierra y de perfil. Explica cómo se representan las proyecciones de cada tipo de recta y provee ejemplos ilustrados.

1. República Bolivariana de Venezuela
Universidad Nacional “Francisco de Miranda”
Núcleo: Los Perozo
Área de Tecnología
Unidad Curricular: Dibujo I
Programa de Ingeniería Civil
Integrantes:
Ckristopher Paz – 26.626.772
Alejandro Parra – 25.254.803
Carlos Pirona – 29.600.575
Tutor(a):
Euridice Torres
SantaAna de Coro, julio de 2021

2. La RECTA es un rastro que deja un punto sobre el espacio cuando este se mueve en una dirección
y pendiente constante. En el espacio la línea recta esta definida, bien sea por dos puntos o un punto y
una dirección. Se acostumbra a denotar la recta con la letra minúscula (a,b,c,k.n.w...)
Toda RECTA en el espacio del sistema diédrico genera automáticamente dos proyecciones en
forma de dos rectas. Una proyección vertical, en el plano de proyección vertical, y otra proyección
horizontal, en el plano de proyección horizontal.
Representación Espacial Representación Descriptiva
Continua procedimiento

3. A
B
A
B
r
Dos (2) puntos “A” y “B” que
pertenece a la Recta “r”
Representación Descriptiva
Proyección de la Recta “r”
A
v
B
v
B
h A
h
A
v
B
v
B
h
A
h
r
h
r
v
Ejemplo de la Representación grafica de la Proyección de la Recta
PV
PH
PV
PH

4. Si tenemos las proyecciones de dos puntos cualesquiera, podemos conseguir las
proyecciones de la recta definida por dichos puntos uniendo sus proyecciones homónimas, esto
es, por un lado las proyecciones verticales y por otro lado las proyecciones horizontales de los
dos puntos.
RECTA HORIZONTAL: es
paralela al plano de proyección
horizontal. Su proyección vertical
es paralela a LT.

5. RECTA FRONTAL: es
paralela al plano de proyección
vertical. Su proyección
horizontal es paralela a LT.

6. RECTA PARALELA A LA
LÍNEA DE TIERRA: sus
proyecciones son paralelas a LT.

7. RECTA DE PIE:
perpendicular al plano horizontal
de proyección. Su proyección
vertical es perpendicular a LT. y
su proyección horizontal queda
representada por un punto.

8. RECTA DE PUNTA:
perpendicular al plano vertical de
proyección. Su proyección
horizontal es perpendicular a LT. y
su proyección vertical queda
representada por un punto.

9. RECTA DE PUNTA:
perpendicular al plano vertical de
proyección. Su proyección
horizontal es perpendicular a LT. y
su proyección vertical queda
representada por un punto.

10. RECTA DE PERFIL:
presenta sus proyecciones
normales a LT por pertenecer a
un plano de perfil.

11. RECTA CONTENIDA EN UN BISECTOR:
sus proyecciones forman un mismo ángulo
con LT.

12. Z (Cota)
P.V. (-)
P.V. (+)
P.H. (+)
P.H. (-) L
T
(x)




 









Y (Vuelo)
A = B
v
Ah
v
Bh
A B
D
C
a
ah
c
Cv
Dv
C
h
Dh
b
b
v
h
Ev
Dv
c
v
bh
E
F
c
Fv
E
h
F
h
T
P.V.
P.H.
A = B
v v
Ah
Bh
ah
Represt.
V.T.
Cv
Dv
C
h Dh
bh
b
v
Represt.
V.T.
Represt.
V.T.
ch
c
v
Ev
Fv
E
h
Fh
Represt.
V.T.
L
Representación Espacial Representación Descriptiva
EJEMPLO DE TIPOS DE RECTA
EN POSICIÓN PARALELA AL PLANO HORIZONTAL
EJEMPLO
Recta de Punta:
Las coordenadas X y Z de los puntos A y B
son Iguales
a { A (15;05;25) @=0º
{ B (15;25;25) ß=90º
Recta Paralela a la línea de tierra:
Las coordenadas Y y Z de los puntos C y D
son Iguales
b { C (20;20;25) @= 0º
{ D (40;20;25) ß= 0º
Recta Horizontal:
Las coordenadas Z de los puntos E y F son
Iguales
c { E (50;05;15) @ = 0º
{ F (60;25;15) 0<ß<90º

13. Representación Espacial Representación Descriptiva
EJEMPLO DE TIPOS DE RECTA
EN POSICIÓN PARALELA AL PLANO VERTICAL
Z (Cota)
P.V. (-)
P.V. (+)
P.H. (+)
P.H. (-) L
(x)




 









Y (Vuelo)
G
v
h
H
G
d
e
I v
Jv
I
h
J h
v
h
I
J
d
v
H
v
G = H
h
e
e
D
C
Cv
Dv
C
h
Dh
b
b
v
h
b
L T
P.V.
P.H.
G = H
h h
G
H
v
dv
Represt.
V.T.
Cv
Dv
C
h Dh
bh
b
v
Represt.
V.T.
Represt.
V.T.
eh
e
v
I v
Jv
I h
J h
Represt.
V.T.
v
EJEMPLO
Recta de Pie:
Las coordenadas X y Y de los puntos G y H
son Iguales
d { G (15;25;05) @= 90º
{ H (15;25;25) ß= 0º
Recta Paralela a la línea de tierra:
Las coordenadas Y y Z de los puntos C y D
son Iguales
b { C (20;20;25) @= 0º
{ D (40;20;25) ß= 0º
Recta Frontal:
Las coordenadas Y de los puntos I y J son
Iguales
e { I (50;25;05) 0<@< 90º
{ J (60;25;25) ß= 0º

14. Recta de perfil: presenta
sus proyecciones normales a
LT por pertenecer a un plano de
perfil.
Y (Vuelo)
Z (Cota)
P.V. (-)
P.V. (+)
P.H. (-)
L
(x)




 









K
P.L.
K'
L'
K
v
L
V
K
h h
L
Ejemplo
Las coordenadas X de los puntos KL son
iguales, su verdadero tamaño se ve en el
Plano Lateral.
g { K (60;05;20)
{ L (60;25;00) @+ ß = 90º
Representación Espacial
Representación Descriptiva
en el Plano Lateral
T
L
P.V. P.L.
P.H.
L
h
L
v
K
h
K
v K
L
l
2
,
8
3
l

































se levantan
perpend. a LT.
V
e
r
d
a
d
e
r
o
T
a
m
a
ñ
o
(
V
.
T
.
)








































Ángulo de la
Recta de Perfil

15. Proyección
lámina Din A4
RECTA DE PERFIL
NOMBRE:
UNIVERSIDAD
C.I.:
FECHA:
SECC:
NOTA:
LT
L
h
L
v
K
h
K
v K
L
l
l
P.L.
Las coordenadas X de los puntos K L son iguales, su
verdadero tamaño se ve en el Plano Lateral.
g { K (60;05;20)
{ L (60;25;00) @+ ß = 90º
V
.
T
.
4
5
°
45°
IDENTIFICAR
NOMBRE:
UNIVERSIDAD
C.I.:
FECHA:
SECC:
NOTA:
LT
L
h
L
v
K
h
K
v K
L
l
l
P.L.
Las coordenadas X de los puntos K L son iguales, su
verdadero tamaño se ve en el Plano Lateral.
g { K (60;05;20) @+ ß = 90º
{ L (60;25;00)
V
.
T
.





































































































































































 

4
5
°
45°
2
.
8
3
m
m