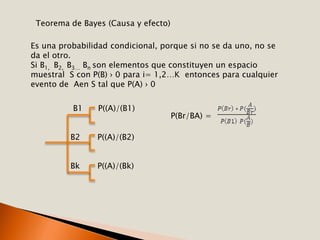
La teoría de probabilidades asigna números a los posibles resultados de experimentos aleatorios para cuantificar la probabilidad de que ocurran ciertos sucesos. Un suceso es cada resultado posible y un espacio muestral es el conjunto de todos los resultados posibles. La regla de adición establece cómo calcular la probabilidad de la unión de sucesos y la regla de multiplicación se usa para sucesos condicionados. El teorema de Bayes calcula probabilidades condicionales cuando se conocen las causas y efectos de diferentes resultados.

1. Lcda. Gladys Sánquiz

2. La teoría de probabilidades: se ocupa de asignar un cierto
número a cada posible resultado que pueda ocurrir en un
experimento aleatorio, con el fin de cuantificar dichos
resultados y saber si un suceso es más probable que otro
Suceso: Es cada uno de los resultados posibles de una
experiencia aleatoria. Tambien se puede definir como una
parte del estacio muestral.
Ejemplo : Al tirar un dado un suceso sería salir par
Espacio muestral: Es el conjunto de todos los posibles
resultados que puedes darse al ocurrir un experimento
aleatorio. Se representa por E (o bien por la letra griega “Ω” )
Ejemplo :Una bolsa contiene bolas blancas y negras. Se
extraen sucesivamente tres bolas. Calcular:
El espacio muestral.
Ω={(bbb); (bbn); (bnb); (nbb); (bnn); (nbn), (nnb); (nnn)}

3. Suceso A {extraer tres bolas del mismo color}
P(a)={(bbb); (nnn)} 2/8=0,25
0,25 *100= 25%
Regla de la adición
Si A y B son eventos
P(A⋃B) = P(A) + P(B) − P(A⋂B)
Ejemplo
Se hizo una encuesta a la ciudad sobre medio de transporte y se
encontró que 70% usa servicios públicos de transporte, 40% usan
transporte particular y que 30% usan ambos tipos. Calcular la
probabilidad de que se use algún tipo de transporte.
P(A⋃B) = P(0,70) + P(0,40) − P(0,30) =0,80
0,80 *100=80%.
El 80% utiliza transporte y el 20% no lo usa.

4. Regla de la multiplicación
Si A y B son eventos cualquiera en un espacio mueltral S y P(A) ≠0
Laurna A contiene 4 pelotas rojas y 3 azules mientras que l urna
B contiene 8 pelotas rojas y 2 azules. Se toma 1 pelota de la
urna A sin ver su colory se coloca en la urna B.
Calcular la probabilidad que ambas pelotas elegidas de las urmas
sean rojas
P(1R ⋂ 2R)
P(A ⋂ B)= P(A) * p(B/A)
P(2R/1R) 9/11 P=(1R ⋂ 2R)
P (1R) 4/7
P(2A/1R) 2/11 P=(1R)*(2R)
P=(4/7 * 9/11)
P(2R/1A) 8/11 36/77=0,47
P (1R) 4/7
P(2A/1A) 3/11

5. Teorema de Bayes (Causa y efecto)
Es una probabilidad condicional, porque si no se da uno, no se
da el otro.
Si B1, B2, B3… Bn son elementos que constituyen un espacio
muestral S con P(B) › 0 para i= 1,2…K entonces para cualquier
evento de Aen S tal que P(A) › 0
B1 P((A)/(B1)
B2 P((A)/(B2)
Bk P((A)/(Bk)
P(Br/BA) =

6. Ejemplo.
Hay 2 métodos A y B para enseñar cierta destreza industrial el porcentaje de
fracasos del método A es del 20%, el del método B es del 10% .
Sin embargo como en el método b es más caro, sólo se aplica en 30% (el
otro 70% se aplica A), Una trabajadora recibio capacitación por unp de los
métodos pero no aprendió la destreza. ¿Cuál es la probabilidad de que se le
hayan enseñado con el método A?
P(A)=70% P FA=0,20 P(A/F) =P(A) (PF/A) _____
P(A) P(F/A) + P(B) P(F/B)
P(B)=30% P FA=0,20 = 0,70 * 0,20_______________
(0,70 *0,20) + (0,30 *0,10)
P(A/F) = 0,14________ = 0,82
(0,14 + 0,03)
La probabilidad que le hayan enseñado con el métod A
es del 82%