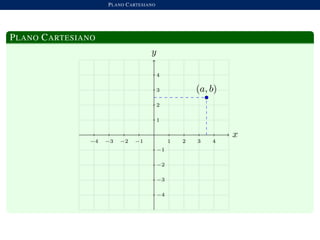
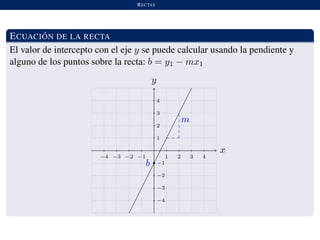
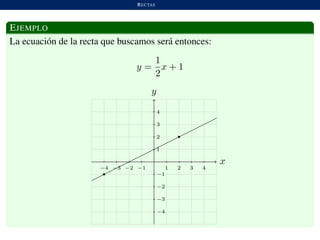
Este documento describe el plano cartesiano y las ecuaciones de líneas rectas. Explica cómo los puntos en un plano se pueden identificar con pares ordenados de números para formar el plano cartesiano. También define las ecuaciones de líneas rectas, incluyendo la pendiente, el intercepto con el eje y, líneas paralelas y perpendiculares. Además, incluye ejemplos y ejercicios para ilustrar estos conceptos.

2. PLANO CARTESIANO Y LINEAS RECTAS
Diego Sandoval
Departamento de Matem´aticas, F´ısica y Estad´ıstica
Universidad de La Sabana

3. PLANO CARTESIANO
PLANO CARTESIANO
Los puntos en un plano se pueden identificar con pares ordenados de n´umeros
para formar el plano coordenado o plano cartesiano.
Para hacer esto, trazamos dos rectas reales perpendiculares que se cruzan en 0
en cada recta.
Por lo general, una recta es horizontal con direcci´on positiva a la derecha y se
llama eje x; la otra recta es vertical con direcci´on positiva hacia arriba y se
denomina eje y. El punto de intersecci´on del eje x y el eje y es el origen O

4. PLANO CARTESIANO
PLANO CARTESIANO
x
−4 −3 −2 −1 1 2 3 4
y
(a, b)
−4
−3
−2
−1
1
2
3
4

5. PLANO CARTESIANO
CUADRANTES
x
y
III
III IV
Este sistema de coordenadas recibe el
nombre de sistema de coordenadas
rectangulares o sistema de
coordenadas cartesianas en honor al
matem´atico franc´es Ren´e Descartes
(1596-1650). El plano provisto con
este sistema de coordenadas se llama
plano coordenado o plano cartesiano
y se denota con R2.
Los ejes x y y se denominan ejes
coordenados y dividen el plano
cartesiano en cuatro cuadrantes,
marcados I, II, III y IV en la figura.
Note que el primer cuadrante est´a
formado por los puntos cuyas
coordenadas x y y son positivas.

6. RECTAS
RECTAS
ECUACI ´ON DE LA RECTA
La ecuaci´on de una recta no vertical que pasa por los puntos A(x1, y1) y
B(x2, y2) tiene por ecuaci´on:
y = mx + b
Donde al valor m se le llama la pendiente de la recta y al valor b intercepto
con el eje y.
Podemos conocer el valor de la pendiente si conocemos las coordenadas los
puntos A y B sobre la recta. Se calcula m como:
m =
y2 − y1
x2 − x1

7. RECTAS
ECUACI ´ON DE LA RECTA
El valor de intercepto con el eje y se puede calcular usando la pendiente y
alguno de los puntos sobre la recta: b = y1 − mx1
x
−4 −3 −2 −1 1 2 3 4
y
b
m
−4
−3
−2
−1
1
2
3
4

8. RECTAS
EJEMPLO
Encontrar la ecuaci´on de la recta que pasa por los puntos A(−4, −1) y B(2, 2)
Primero calculamos la pendiente la recta:
m =
y2 − y1
x2 − x1
=
2 − (−1)
2 − (−4)
=
1
2
Luego calculamos el punto de intersecci´on con el eje y:
b = y1 − mx1 = −1 −
1
2
(−4)
= −1 + 2
= 1

9. RECTAS
EJEMPLO
La ecuaci´on de la recta que buscamos ser´a entonces:
y =
1
2
x + 1
x
−4 −3 −2 −1 1 2 3 4
y
−4
−3
−2
−1
1
2
3
4

10. RECTAS
EJERCICIOS
Determine la ecuaci´on de la recta que satisface las indicaciones dadas en cada
caso, luego grafique cada recta:
Pasa por los puntos A(−2, 2) y B(3, −1)
Pasa por el punto A(1, 1) y tiene pendiente m = 3
Pasa por el punto A(−3, −1) y corta al eje y en -2
Corta al eje x en 3; y al eje y en -5
Pasa por los puntos A(−2, 2) y B(3, 2)
Pasa por los puntos A(−2, 2) y B(−2, −1)

11. RECTAS
RECTAS PARALELAS
RECTAS PARALELAS
Dos lineas rectas son paralelas si mantienen una equidistancia entre si, es
decir, nunca se cortan la una a la otra.
Para que dos rectas L1 : y = m1x + b1 y L2 : y = m2x + b2 sean paralelas
deben tener la misma pendiente, es decir: m1 = m2
x
−4 −3 −2 −1 1 2 3 4
y
paralelas
−4
−3
−2
−1
1
2
3
4

12. RECTAS
RECTAS PERPENDICULARES
RECTAS PERPENDICULARES
Dos lineas rectas son perpendiculares si se cortan formando un ´angulo recto.
Para que dos rectas L1 : y = m1x + b1 y L2 : y = m2x + b2 sean
perpendiculares, sus pendientes deben cumplir: m1 · m2 = −1
x
−4 −3 −2 −1 1 2 3 4
y
perpendiculares
−4
−3
−2
−1
1
2
3
4

13. RECTAS
EJERCICIOS
Determine la ecuaci´on de la recta que satisface las indicaciones dadas en cada
caso, luego grafique:
Pasa por el punto A(1, 1) y es paralela a la recta y = 2x − 5
Pasa por el punto A(−3, −1) y es perpendicular a la recta y = 1
3x − 2
Es paralela a la recta y = 2x − 5, y pasa por el punto de intersecci´on
entre la recta y = x + 5 con la recta y = −2x − 1