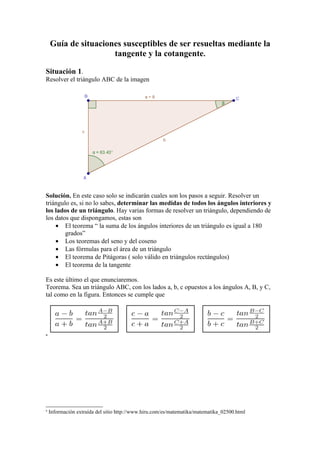
Este documento presenta 4 situaciones que pueden resolverse usando tangentes y cotangentes. La primera involucra resolver un triángulo usando el teorema de la tangente. La segunda calcula la distancia recorrida por un bote basado en cambios en su ángulo de depresión. La tercera diseña una ruta de ferrocarril y calcula su longitud total. La cuarta determina si dos funciones son iguales basado en su dominio.

1. Guía de situaciones susceptibles de ser resueltas mediante la
tangente y la cotangente.
Situación 1.
Resolver el triángulo ABC de la imagen
Solución. En este caso solo se indicarán cuales son los pasos a seguir. Resolver un
triángulo es, si no lo sabes, determinar las medidas de todos los ángulos interiores y
los lados de un triángulo. Hay varias formas de resolver un triángulo, dependiendo de
los datos que dispongamos, estas son
• El teorema “ la suma de los ángulos interiores de un triángulo es igual a 180
grados”
• Los teoremas del seno y del coseno
• Las fórmulas para el área de un triángulo
• El teorema de Pitágoras ( solo válido en triángulos rectángulos)
• El teorema de la tangente
Es este último el que enunciaremos.
Teorema. Sea un triángulo ABC, con los lados a, b, c opuestos a los ángulos A, B, y C,
tal como en la figura. Entonces se cumple que
a
a
Información extraída del sitio http://www.hiru.com/es/matematika/matematika_02500.html

2. .
Situación 2.b
Desde lo alto de un edificio situado frente a un océano, un observador ve un bote que
navega directamente hacia el edificio. Si el observador está a 30,5 metros sobre el nivel
del mar y si el ángulo de depresión del bote cambia de 25º a 40º durante el periodo de
observación, calcula la distancia que recorre el bote.
Solución. Como en la figura, sean A y B las posiciones del bote que corresponden a los
ángulos de 25º y 40º, respectivamente. Suponga que el observador está en el punto D, y
C es el punto 30,5 metros directamente abajo.
Denota con d la distancia que recorre el bote, y denote con k la distancia de B a C. Si
alpha y beta denotan los ángulos DAC y DBC, respectivamente, Entonces se deduce por
geometría (ángulos alternos internos) que α = 25º y β = 40º.
Del triángulo BCD
cot (β) = cot (40º) = k/30.5
k=30.5 cot (40º)
Del triángulo DAC
cot (α)= cot (25º) = ( d + k )/30.5
d + k = 30.5 cot (25º)
d = 30.5 cot (25º) - k
=30.5 cot (25º) – 30.5 (cot 40º)
= 30.5 (cot (25º) - cot (40º))
≈30.5(2.145 – 1.192) ≈ 29.06
b
Swokowski, Earl. Algebra y trigonometría con geometría analítica. Cengage Learning. Ed. 2009. Página
482

3. En consecuencia, el bote recorre aproximadamente 29 metros.
Situación 3c
Planeación de una ruta de ferrocarril.
En la figura se muestra una ruta de ferrocarril propuesta que pasa por tres ciudades,
localizadas en los puntos A, B y C. En B, la vía da vuelta hacia C en un ángulo theta.
a) Demuestre que la distancia total d de A a C está dada por d =20 tan (θ/2) +40 (d
es la longitud total de la ruta del ferrocarril).
b) Debido a las montañas entre A y C, el punto de inflexión B debe estar alejado al
menos 20 millas de A. ¿Hay una ruta que evite las montañas y mida exactamente
50 millas?
Solución. a) Nota que la longitud de la vía férrea de A hasta C es la suma de la longitud
entre A y B, más la longitud entre B y C. La distancia final de la línea ferroviaria entre
A y C depende del ángulo θ, el cual es desconocido, pero sabemos que es forzosamente
un ángulo agudo, al ser un ángulo interior de un triángulo rectángulo.
Llamemos O al vértice en que se forma el ángulo recto. Tenemos entonces el siguiente
esquema
c
Swokowski, Earl. Algebra y trigonometría con geometría analítica. Cengage Learning. Ed. 2009.
Página 542.

4. Para determinar la distancia x entre B y C – que llamaremos d(B,C)-, tenemos que
Un argumento similar nos permite determinar la longitud y
Para encontrar d(A,B), nada más notar que esta distancia es 40- y, o lo que es lo mismo
Así, la distancia vial entre A y C, esto es, d(A,C) = d (A,B)+d(B,C), o sea
Donde lo encerrado en paréntesis puede arreglarse con la formula para el ángulo mitad,
quedando finalmente como
Con lo que hemos demostrado lo pedido.
b) Dicho de otra manera, se nos pregunta si existe un ángulo θ, agudo, tal que
40 +20 tan (θ/2)=50
Luego de algunos despejes elementales, se tiene que el ángulo θ debe cumplir la
ecuación

5. Puesto que para un ángulo agudo, la tangente toma todos los valores positivos, esta
claro que tal ángulo θ existe.
Por medio de la calculadora, puede aproximarse su valor en radianes a
.
Situación 4.
Supón que las siguientes funciones están definidas en el mayor intervalo posible de los
números reales:
¿Son f(x) y g(x) la misma función? Explica claramente tu argumento, demostrando su
igualdad en caso de ser la misma función, o bien entregando un contraejemplo si son
funciones diferentes.
Solución. Un primer intento sería graficar ambas funciones, a ver como nos va.
Con f(x):
Y ahora con g(x):

6. Salvo la evidente diferencia en el color, ambas funciones parecen tener la misma
gráfica.
Un intento de demostración de la aparente igualdad puede construirse así:
Pero esta demostración es falsa.
La razón es simple, pero sublime para un inexperto. Sabemos que cot(x)= 1/tan(x),
siempre que el denominador sea distinto de cero. Luego la función f(x) estará bien
definida mientras la cotangente no se indetermine en ningún punto del dominio.
Las gráficas de f(x) y de g(x) parecen la misma, por que la gran mayoría de los
procesadores geométricos no son capaces de reconocer los puntos en que f(x) se
indetermina. Pero dichos puntos existen. Es mas, hay infinitos puntos de este
tipo..Cualquier valor de x en el que se cumpla que
es un punto que no pertenece al dominio de f(x), pero que si pertenece al de
g(x).Como ejemplo, verifica si existe f(π).
Este es un claro ejemplo que muestra que, aunque los procesadores geométricos son
muy poderosos, tienen fallas, por lo que el análisis matemático debe imponerse sobre
cualquier justificación gráfica.d
d
Marerial preparado por Héctor Mena Sandoval.