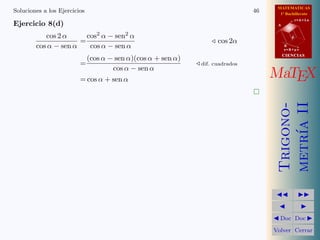
El documento trata sobre las razones trigonométricas de la suma de ángulos. Explica cómo calcular sen(α+β), cos(α+β) y tan(α+β) en términos de senα, cosα, senβ y cosβ. Además, presenta un ejemplo numérico para calcular sen75°, cos75° y tan75° a partir de los valores de sen30° y sen45°.

1. MATEMATICAS
1º Bachillerato
MaTEX
r=A+lu
Proyecto A
d
Razones B
s=B+mv
CIENCIAS
Trigonom´tricas II
e MaTEX
Fco Javier Gonz´lez Ortiz
a
metr´ II
Trigono-
ıa
Directorio
Tabla de Contenido
Inicio Art´
ıculo
c
2004 javier.gonzalez@unican.es Doc Doc
D.L.:SA-1415-2004 ISBN: 84-688-8267-4
Volver Cerrar

2. MATEMATICAS
1º Bachillerato
Tabla de Contenido A
r=A+lu
1. Razones trigonom´tricas de ..
e d
1.1. Suma de ´ngulos
a B
s=B+mv
1.2. Diferencia de ´ngulos
a CIENCIAS
1.3. El ´ngulo doble
a
´
1.4. Angulo mitad MaTEX
2. Ecuaciones trigonom´tricas
e
3. Ampliaci´no
3.1. Suma y diferencia de senos
metr´ II
Trigono-
3.2. Suma y diferencia de cosenos
3.3. Ejercicios
ıa
Soluciones a los Ejercicios
Doc Doc
Volver Cerrar

3. MATEMATICAS
Secci´n 1: Razones trigonom´tricas de ..
o e 3 1º Bachillerato
1. Razones trigonom´tricas de ..
e
r=A+lu
A
1.1. Suma de ´ngulos
a d
Se trata de calcular las razones de (α + β) en funci´n de las razones de α
o B
s=B+mv
y β. CIENCIAS
En la figura se tiene que
OA = cos β AB = sen β B M
MaTEX
Se tiene as´ que
ı,
metr´ II
Trigono-
sen(α + β) =P B = N M
=N A + AM
ıa
=OA sen α + AB cos α
= sen α cos β + cos α sen β A
β
cos(α + β) =OP = ON − P N α
=ON − BM
0 P N
=OA cos α − AB sen α
= cos β cos α − sen β sen α
Doc Doc
Volver Cerrar

4. MATEMATICAS
Secci´n 1: Razones trigonom´tricas de ..
o e 4 1º Bachillerato
Para calcular la tan(α + β) realizamos el cociente del seno entre el coseno
r=A+lu
A
sen(α + β)
tan(α + β) =
d
cos(α + β) B
s=B+mv
sen α cos β + cos α sen β CIENCIAS
=
cos α cos β − sen α sen β
=(dividiendo por cos α cos β) MaTEX
tan α + tan β
=
1 − tan α tan β
metr´ II
Trigono-
Razones de la suma de ´ngulos
a
ıa
sen(α + β) = sen α cos β + cos α sen β
cos(α + β) = cos β cos α − sen β sen α
(1)
tan α + tan β
tan(α + β) =
1 − tan α tan β
Doc Doc
Volver Cerrar

5. MATEMATICAS
Secci´n 1: Razones trigonom´tricas de ..
o e 5 1º Bachillerato
Ejemplo 1.1. A partir de 30o y 45o obtener el valor exacto de sen 75o ,cos 75o
r=A+lu
A
y tan 75o .
d
Soluci´n:
o B
s=B+mv
sen 75o = sen(30 + 45) = sen 30 cos 45 + cos 30 sen 45 CIENCIAS
√ √ √
1 2 3 2
= ·
2 2√ 2
√
+ ·
2 MaTEX
2+ 6
=
4
metr´ II
Trigono-
cos 75o = cos(30 + 45) = cos 30 cos 45 − sen 30 sen 45
√ √ √
3 2 1 2
ıa
= · − ·
√2 2
√ 2 2
6− 2
=
4
tan 30 + tan 45
tan 75o = tan(30 + 45) =
1 − tan 30 tan 45
√ √
(1/ 3) + 1 1+ 3
= √ =√
1 − (1/ 3) 3−1
Doc Doc
Volver Cerrar

6. MATEMATICAS
Secci´n 1: Razones trigonom´tricas de ..
o e 6 1º Bachillerato
1.2. Diferencia de ´ngulos
a
r=A+lu
A
Utilizando las razones de los ´ngulos opuestos y utilizando las f´rmulas
a o d
para la suma de ´ngulos se obtiene:
a B
s=B+mv
CIENCIAS
sen(α − β) = sen[α + (−β)]
= sen α cos(−β) + cos α sen(−β) MaTEX
= sen α cos β − cos α sen β
cos(α − β) = cos[α + (−β)]
metr´ II
Trigono-
= cos α cos(−β) − sen α sen(−β)
ıa
= cos α cos β + sen α sen β
tan(α − β) = tan[α + (−β)]
tan α + tan(−β)
=
1 − tan α tan(−β)
tan α − tan β
=
1 + tan α tan β
Doc Doc
Volver Cerrar

7. MATEMATICAS
Secci´n 1: Razones trigonom´tricas de ..
o e 7 1º Bachillerato
La diferencia de ´ngulos
a
r=A+lu
A
d
sen(α − β) = sen α cos β − cos α sen β B
s=B+mv
cos(α − β) = cos β cos α + sen β sen α CIENCIAS
(2)
tan α − tan β
tan(α − β) =
1 + tan α tan β MaTEX
Ejemplo 1.2. A partir de 30o y 45o hallar sen 15o y cos 15o .
Soluci´n:
o
metr´ II
Trigono-
sen 15o = sen(45 − 30) = sen 45 cos 30 − cos 45 sen 30
√ √ √
ıa
2 3 2 1
= −
√2 2√ 2 2
6− 2
=
4
cos 15o = cos(45 − 30) = cos 45 cos 30 + sen 30 sen 45
√ √ √
2 3 1 2
= +
√ 2√ 2 2
2
6+ 2
=
4
Doc Doc
Volver Cerrar

8. MATEMATICAS
Secci´n 1: Razones trigonom´tricas de ..
o e 8 1º Bachillerato
1.3. El ´ngulo doble
a
r=A+lu
A
A partir de las razones de la suma obtenemos: d
sen(2 α) = sen[α + α] = sen α cos α + cos α sen α B
s=B+mv
CIENCIAS
=2 sen α cos α
cos(2 α) = cos[α + α] = cos α cos α − sen α sen α MaTEX
= cos α − sen α
2 2
tan α + tan α
metr´ II
tan(2 α) = tan[α + α] =
Trigono-
1 − tan α tan α
2 tan α
ıa
=
1 − tan2 α
Razones del ´ngulo doble
a
sen(2 α) = 2 sen α cos α
cos(2 α) = cos2 α − sen2 α
(3)
2 tan α
tan(2 α) = Doc Doc
1 − tan2 α
Volver Cerrar

9. MATEMATICAS
Secci´n 1: Razones trigonom´tricas de ..
o e 9 1º Bachillerato
Ejemplo 1.3. A partir de las razones de 60o hallar sen 120o y cos 120o .
r=A+lu
A
Soluci´n:
o d
sen 120o = sen(2 · 60) =2 sen 60 cos 60 B
s=B+mv
√ √ CIENCIAS
3 1 3
=2 · =
2 2 2
cos 120o = cos(2 · 60) = cos2 60 − sen2 60 MaTEX
1 3 1
= − =−
4 4 2
metr´ II
Trigono-
1
Ejemplo 1.4. Si α est´ en el tercer cuadrante y cos α = − , obtener el valor
a
ıa
2
de sen 2 α y cos 2 α .
Soluci´n: Primero calculamos sen α
o
√
1 2 3 3
sen α = 1 − cos α = 1 − ( ) = =⇒ sen α = −
2 2
2 4 2
√ √
3 1 3
sen 2 α =2 sen α cos α = 2 · · =
2 2 2
1 3 1
cos 2 α = cos2 α − sen2 α = − = −
4 4 2
Doc Doc
Volver Cerrar

10. MATEMATICAS
Secci´n 1: Razones trigonom´tricas de ..
o e 10 1º Bachillerato
´
1.4. Angulo mitad A
r=A+lu
A partir del coseno del ´ngulo doble se tiene
a d
α α α B
cos 2 ( ) = cos2 − sen2 (4) s=B+mv
2 2 2 CIENCIAS
α
cos α = 1 − 2 sen2 (5)
2
α
cos α = 2 cos2 − 1 (6)
MaTEX
2
Despejando en las dos ultimas expresiones obtenemos las razones del seno y
coseno para el ´ngulo mitad
a
metr´ II
Trigono-
α 1 − cos α
sen2 = (7)
ıa
2 2
α 1 + cos α
cos2
= (8)
2 2
Dividiendo las dos expresiones anteriores
α 1 − cos α
tan2 = (9)
2 1 + cos α
Doc Doc
Volver Cerrar

11. MATEMATICAS
Secci´n 1: Razones trigonom´tricas de ..
o e 11 1º Bachillerato
Ejemplo 1.5. Con el ´ngulo mitad obtener el valor exacto de sen 15o ,
a
r=A+lu
A
cos 15o y tan 15o .
d
Soluci´n:
o B
√ √
s=B+mv
1 − cos 30 1 − 23 2− 3
CIENCIAS
sen 15 =
2 o
= =⇒ sen 15 =
o
2 2 4
√ √
MaTEX
1 + cos 30 1 + 23 2+ 3
cos 15 =
2 o
= =⇒ cos 15o =
2 2 4
metr´ II
Trigono-
√ √
1 − cos 30 1 − 23 2− 3
tan 15 =
2 o
= √ =⇒ tan 15 =
o
√
1 + cos 30
ıa
1 + 23 2+ 3
1
Ejercicio 1. Si α est´ en el tercer cuadrante y cos α = − , obtener el valor
a
5
α α α
de sen , cos y tan .
2 2 2
Doc Doc
Volver Cerrar

12. MATEMATICAS
Secci´n 2: Ecuaciones trigonom´tricas
o e 12 1º Bachillerato
2. Ecuaciones trigonom´tricas
e
r=A+lu
A
Llamamos ecuaci´n trigonom´trica a una ecuaci´n con razones trigonom´tri-
o e o e d
cas, donde se pretende calcular el ´ngulo inc´gnita α. No hay un m´todo
a o e B
s=B+mv
general de resoluci´n pero podemos indicar algunas pautas de resoluci´n,
o o CIENCIAS
como:
Sacar factor com´n cuando el t´rmino independiente es cero.
u e MaTEX
Procurar que todas las razones tengan el mismo angulo.
´
Y procurar obtener la misma raz´n trigonom´trica
o e
metr´ II
Trigono-
ıa
Doc Doc
Volver Cerrar

13. MATEMATICAS
Secci´n 2: Ecuaciones trigonom´tricas
o e 13 1º Bachillerato
1 r=A+lu
Ejemplo 2.1. Resolver la ecuaci´n cos α =
o A
2
1 d
Soluci´n: Conocemos que cos 60o =
o .
2
B
s=B+mv
Dibujamos un aspa como el de la figura a partir de 60o y obtenemos las CIENCIAS
soluciones entre 0 y 360.
A estas soluciones se le a˜aden un m´ltiplo cualquiera de vueltas con la
o
n
u
u
expresi´n 360o k, siendo k un n´mero entero.
MaTEX
y
1 α = 60o + 360o k
cos α = =⇒ π−α α = 60
metr´ II
Trigono-
2 α = 300o + 360o k

ıa
 α = π + 2kπ

 3
=⇒

 α = 5π
 + 2kπ 0 x
3
π+α 2π − α
Las soluciones las puedes expresar en grados o en radianes
Doc Doc
Volver Cerrar

14. MATEMATICAS
Secci´n 2: Ecuaciones trigonom´tricas
o e 14 1º Bachillerato
√
Ejemplo 2.2. Resolver la ecuaci´n tan α = − 3
o
r=A+lu
A
√
Soluci´n: Conocemos que tan 60o = 3.
o d
Dibujamos un aspa como el de la figura a partir de 60o y obtenemos las solu- B
ciones entre 0 y 360.
s=B+mv
CIENCIAS
y
tan α = −
√
3 =⇒
α
α
= 120o + 360o k
= 300o + 360o k
π−α α = 60 MaTEX


 α 2π

 = + 2 kπ
metr´ II
Trigono-
3
=⇒

 α 5π 0 x

 = + 2kπ
ıa
3
π+α 2π − α
En este caso como entre dos soluciones consecutivas hay 180o , todas las solu-
ciones se pueden expresar de la forma
2π
α= + kπ
3
Doc Doc
Volver Cerrar

15. MATEMATICAS
Secci´n 2: Ecuaciones trigonom´tricas
o e 15 1º Bachillerato
√
2
r=A+lu
Ejemplo 2.3. Resolver la ecuaci´n cos α = −
o
A
√ 2 d
2
Soluci´n: Conocemos que cos 45o =
o . B
2
s=B+mv
Dibujamos un aspa como el de la figura a partir de 45o y obtenemos las solu-
CIENCIAS
ciones entre 0 y 360 donde el coseno es negativo
√
MaTEX
y
2 α = 135 + 360 k o o
cos α = − =⇒
2 α = 225o + 360o k π−α α = 45
metr´ II
Trigono-

 α = 3 π + 2 kπ



4
ıa
=⇒

 α = 5π 0 x

 + 2kπ
4
π+α 2π − α
Doc Doc
Volver Cerrar

16. MATEMATICAS
Secci´n 2: Ecuaciones trigonom´tricas
o e 16 1º Bachillerato
Ejercicio 2. Resolver las ecuaciones trigonom´tricas:
e
r=A+lu
A
√
1 3 1
a) sen α = b) sen 2α = c) cos 3α = d
2 2 2 B
s=B+mv
Ejercicio 3. Resolver las ecuaciones trigonom´tricas:
e CIENCIAS
1 α 1
a) cos 2α = − b) tan = 1 c) cot(α − π) = − √
2 4 3 MaTEX
Ejercicio 4. Resolver las ecuaciones trigonom´tricas:
e
√
a) sec 2 α = 2 b) sen x = 3 cos x c) sen(2 α − 135o ) = 0
metr´ II
Trigono-
Ejercicio 5. Resolver las ecuaciones trigonom´tricas:
e
2 α
√
a) tan 3 α = −1 b) cosec =1 c) 2 cos 2 α = 3
ıa
4
Ejercicio 6. Resolver las ecuaciones trigonom´tricas:
e
(a) sen 2α = sen α (b) cos 2α = cos α
(c) sen α = cos α (d) cos α = cot α
√
(e) tan α = 2 sen α (f) sen α + 3 cos α = 0
(g) 2 sen(α − 30 ) = −1
o
(h) sen 2α cosec α = tan α + sec α Doc Doc
Volver Cerrar

17. MATEMATICAS
Secci´n 2: Ecuaciones trigonom´tricas
o e 17 1º Bachillerato
Ejercicio 7. Resolver las ecuaciones trigonom´tricas:
e
r=A+lu
A
d
(a) 2 − sen x = cos2 x + 7 sen2 x B
s=B+mv
CIENCIAS
(b) 2 sen2 x + 3 cos x = 0
MaTEX
(c) sen x + cos x = 1
metr´ II
Trigono-
(d) sen2 x + cos x + 1 = 0
ıa
√
(e) sen x + cos x = 2
(f) sen 2x − 2 sen 4x = 0
(g) 2 sen(α − 30o ) = −1
(h) sen 2α cosec α = tan α + sec α
Doc Doc
Volver Cerrar

18. MATEMATICAS
Secci´n 3: Ampliaci´n
o o 18 1º Bachillerato
3. Ampliaci´n
o
r=A+lu
A
3.1. Suma y diferencia de senos d
Del seno de la suma y diferencia de ´ngulos :
a B
s=B+mv
CIENCIAS
sen(α + β) = sen α cos β + cos α sen β
sen(α − β) = sen α cos β − cos α sen β
MaTEX
Si sumamos y restamos las dos identidades obtenemos
sen(α + β) + sen(α − β) = 2 sen α cos β
(10)
metr´ II
Trigono-
sen(α + β) − sen(α − β) = 2 cos α sen β
ıa
Si llamamos A = α + β y B = α − β las anteriores identidades son:
A+B A−B
sen A + sen B = 2 sen cos
2 2 (11)
A+B A−B
sen A − sen B = 2 cos sen
2 2
Doc Doc
Volver Cerrar

19. MATEMATICAS
Secci´n 3: Ampliaci´n
o o 19 1º Bachillerato
3.2. Suma y diferencia de cosenos
r=A+lu
A
Del seno de la suma y diferencia de ´ngulos :
a d
B
cos(α + β) = cos α cos β − sen α sen β s=B+mv
CIENCIAS
cos(α − β) = cos α cos β + sen α sen β
Si sumamos y restamos las dos identidades obtenemos MaTEX
cos(α + β) + cos(α − β) = 2 cos α cos β
(12)
cos(α + β) − cos(α − β) = −2 sen α sen β
metr´ II
Trigono-
Si llamamos A = α + β y B = α − β las anteriores identidades son:
ıa
A+B A−B
cos A + cos B = 2 cos cos
2 2 (13)
A+B A−B
cos A − cos B = −2 sen sen
2 2
Doc Doc
Volver Cerrar

20. MATEMATICAS
Secci´n 3: Ampliaci´n
o o 20 1º Bachillerato
Ejemplo 3.1. Convertir en productos las expresiones.
r=A+lu
A
a) sen 3x + sen x b) sen 3x − sen x d
c) cos 3x + cos x d ) cos 3x − cos x B
s=B+mv
CIENCIAS
e) cos 4x + cos 2x f ) cos 4x − cos 2x
g) cos 4x + cos 2y h) sen 2x + sen 2y MaTEX
Soluci´n:
o
a) sen 3x + sen x = 2 sen 2x cos x
metr´ II
Trigono-
b) sen 3x − sen x = 2 cos 2x sen x
c) cos 3x + cos x = 2 cos 2x cos x
ıa
d ) cos 3x − cos x = −2 sen 2x sen x
e) cos 4x + cos 2x = 2 cos 3x cos x
f ) cos 4x − cos 2x = −2 sen 3x sen x
g) cos 4x + cos 2y = 2 cos(2x + y) cos(2x − y)
h) sen 2x + sen 2y = 2 sen(x + y) cos(x − y)
Doc Doc
Volver Cerrar

21. MATEMATICAS
Secci´n 3: Ampliaci´n
o o 21 1º Bachillerato
3.3. Ejercicios
r=A+lu
A
Ejercicio 8. Simplificar las siguientes expresiones:
d
1 − cos 2 α 1 + cos 2 α
B
s=B+mv
(a) (b)
cos2 α cos2 α
CIENCIAS
1 − cos 2 α cos 2 α
(c)
sen2 α
(d)
cos α − sen α MaTEX
Ejercicio 9. Simplificar las siguientes expresiones:
(a) sen(45 + β) + cos(45 + β)
metr´ II
Trigono-
(b) sen(30 + β) + cos(60 + β)
(c) sen(30 + x) + sen(30 − x)
ıa
(d) cos(30 + x) − cos(30 − x)
Ejercicio 10. Demostrar la siguiente identidad:
sen 3x cos 3x
− =2
sen x cos x
2
Ejercicio 11. Si tan 2α = y α es del 3o cuadrante, hallar tan α
3
Ejercicio 12. ¿Existe alg´n ´ngulo menor de 360o cuya tangente sea igual
u a
a su cotangente?
Doc Doc
Volver Cerrar

22. MATEMATICAS
Soluciones a los Ejercicios 22 1º Bachillerato
Soluciones a los Ejercicios
r=A+lu
A
Ejercicio 1. Si α est´ en el tercer cuadrante, α/2 est´ en el segundo cuadrante
a a d
1 − cos α 1+ 1 3
B
2 α α s=B+mv
sen = = 5
=⇒ sen = CIENCIAS
2 2 2 2 5
cos2 =
α 1 + cos α
=
1− 15 α
=⇒ cos = −
2 MaTEX
2 2 2 2 5
sen 15 3
tan 15o = =−
metr´ II
Trigono-
cos 15 2
Ejercicio 1
ıa
Doc Doc
Volver Cerrar

23. MATEMATICAS
Soluciones a los Ejercicios 23 1º Bachillerato
Ejercicio 2.
r=A+lu
A
a) d

 α π B

 = + 2kπ s=B+mv
1 α = 30o + 2kπ 6 CIENCIAS
sen α = =⇒ =⇒
2 α = 150o + 2kπ 
 α 5π
= + 2kπ

6 MaTEX
b)

 π  α π
metr´ II
√  = + kπ
Trigono-
3  2α = + 2kπ 
3 6
sen 2α = =⇒ 2π =⇒
2  2α = + 2kπ 
 α π
= + kπ
ıa
3 
3
c)

 π 
 α π 2kπ
 3α = + 2kπ 
 = +
1 3 9 3
cos 3α = =⇒ 5π =⇒
2  3α = + 2kπ 
 5π 2kπ
3  α
 = +
9 3
Ejercicio 2
Doc Doc
Volver Cerrar

24. MATEMATICAS
Soluciones a los Ejercicios 24 1º Bachillerato
Ejercicio 3.
r=A+lu
A
a) d
 
2π  α π B
 2α
 = + 2kπ 
 = + kπ s=B+mv
1 3 3 CIENCIAS
cos 2α = − =⇒ 4π =⇒
2 
 2α 
 α 2π
= + 2kπ = + kπ
3

3 MaTEX
b)
 α π 
 = + 2kπ  α = π + 8kπ
metr´ II
Trigono-
α 4 4
tan = 1 =⇒ =⇒
4  α = 5π + 2kπ  α = 5π + 8kπ
ıa
4 4
1
c) cot(α − π) = − √
3

  5π
 α − π = 2π + 2kπ



 α = + 2kπ
√ 3
tan(α−π) = − 3 =⇒ 3 =⇒
 α − π = 5π + 2kπ
 

 α =
8π
+ 2kπ
3 
3
Ejercicio 3
Doc Doc
Volver Cerrar

25. MATEMATICAS
Soluciones a los Ejercicios 25 1º Bachillerato
Ejercicio 4.
r=A+lu
A
a) sec 2 α = 2 d

 α π B

 = + 2kπ s=B+mv
1 2α = 60o + 2kπ 6 CIENCIAS
cos 2 α = =⇒ =⇒
2 2α = 300o + 2kπ 
 α 5π
= + 2kπ

6 MaTEX
b)
 π
√ √  x = + 2kπ
3
metr´ II
Trigono-
sen x = 3 cos x ⇒ tan x = 3 =⇒
 x = 4π + 2kπ
3
ıa
c)


 3π
2 α − 135o

= 0 + 2kπ  α = +kπ
8
sen(2 α−135o ) = 0 =⇒
2 α − 135o = π + 2kπ 
 α 7π

 = +kπ
8
Ejercicio 4
Doc Doc
Volver Cerrar

26. MATEMATICAS
Soluciones a los Ejercicios 26 1º Bachillerato
Ejercicio 5.
r=A+lu
A
a) d

  π 2kπ B
 3α 3π  α
 = +
s=B+mv
 = + 2kπ 
4 3 CIENCIAS
tan 3 α = −1 =⇒ 4 =⇒

 3α 7π 
 7π 2 k π
= + 2kπ
4
 α
 =
12
+
3 MaTEX
α
b) cosec2 =1
4
 α
metr´ II
Trigono-
 π
 = + 2kπ
α 4 2 α = 2π + 8kπ
sen2 = ±1 =⇒ 3π =⇒
ıa
4  α =
 + 2kπ α = 6π + 8kπ
4 2
√
c) 2 cos 2 α = 3
 
π  α π
√  2α
 = + 2kπ 
 = +kπ
3 6 12
cos 2 α = =⇒ 10π
2  2α
 = + 2kπ 
 α 5π
 = +kπ
3 3
Ejercicio 5
Doc Doc
Volver Cerrar

27. MATEMATICAS
Soluciones a los Ejercicios 27 1º Bachillerato
Ejercicio 6(a)
r=A+lu
A
Utilizamos el seno del ´ngulo doble y sacamos factor com´n:
a u
d
sen 2α = sen α B
s=B+mv
2 sen α cos α = sen α CIENCIAS
2 sen α cos α − sen α =0
sen α (2 cos α − 1) =0 MaTEX

 α = 0 + kπ
sen α = 0 
1 =⇒ π 5π
cos α =
metr´ II
Trigono-
 α =
 + 2kπ + 2kπ
2 3 3
ıa
Doc Doc
Volver Cerrar

28. MATEMATICAS
Soluciones a los Ejercicios 28 1º Bachillerato
Ejercicio 6(b)
r=A+lu
A
Utilizamos el coseno del ´ngulo doble, pasando todo a cosenos y resolvemos
a
d
la ecuaci´n:
o B
s=B+mv
cos 2α = cos α CIENCIAS
cos α − sen2 α = cos α
2
cos2 α − (1 − cos2 α) = cos α MaTEX
2 cos2 α − cos α − 1 =0

 α = 0 + 2kπ
cos α =1 
metr´ II
Trigono-
1 =⇒ 2π 4π
cos α = −  α
 = + 2kπ + 2kπ
2 3 3
ıa
Doc Doc
Volver Cerrar

29. MATEMATICAS
Soluciones a los Ejercicios 29 1º Bachillerato
Ejercicio 6(c)
r=A+lu
A
Expresamos el coseno en funci´n del seno, elevamos al cuadrado y resolvemos
o
d
la ecuaci´n:
o B
s=B+mv
sen α = cos α CIENCIAS
sen α = 1 − sen2 α
sen2 α =1 − sen2 α
MaTEX
2 sen2 α =1
√
1 2
metr´ II
Trigono-
sen α = ± √ = ±
2 2
 √ 
3π
ıa
2  α = π

 sen α =

 + 2kπ + 2kπ
2 4 4
√ =⇒

 sen α =−
2  α = 5π + 2kπ


7π
+ 2kπ
2 4 4
Las que no tienen recuadro son del segundo y cuarto cuadrante que no
cumplen la ecuaci´n inicial. Esto suele ocurrir cuando se eleva al cuadrado o
o
hay denominadores
Doc Doc
Volver Cerrar

30. MATEMATICAS
Soluciones a los Ejercicios 30 1º Bachillerato
Ejercicio 6(d)
r=A+lu
A
Utilizamos la definici´n de la cotangente, operamos y sacamos factor com´n:
o u
d
cos α = cot α B
s=B+mv
cos α
cos α =
CIENCIAS
sen α
cos α sen α = cos α MaTEX
cos α sen α − cos α =0
cos α(sen α − 1) =0

metr´ II
Trigono-
 α π
cos α = 0
 = +k π
=⇒ 2
sen α = 1 π
ıa
 α
 = +2k π
2
La primera soluci´n incluye a la segunda, luego
o
π
α= +k π
2
Doc Doc
Volver Cerrar

31. MATEMATICAS
Soluciones a los Ejercicios 31 1º Bachillerato
Ejercicio 6(e)
r=A+lu
A
Utilizamos la definici´n de la tangente, operamos y sacamos factor com´n:
o u
d
tan α =2 sen α B
s=B+mv
sen α
=2 sen α
CIENCIAS
cos α
sen α =2 sen α cos α MaTEX
sen α (1 − 2 cos α) =0

 α = 0+k π
sen α = 0 
metr´ II
1 =⇒
Trigono-
π 5π
cos α =  α =
 +2k π +2k π
2 3 3
ıa
Doc Doc
Volver Cerrar

32. MATEMATICAS
Soluciones a los Ejercicios 32 1º Bachillerato
Ejercicio 6(f )
r=A+lu
A
Expresamos el coseno en funci´n del seno, elevamos al cuadrado y resolvemos
o
d
la ecuaci´n:
o
√ B
s=B+mv
sen α + 3 cos α =0 CIENCIAS
√
sen α + 3 1 − sen2 α =0
√
3 1 − sen2 α = − sen α
MaTEX
3 (1 − sen2 α) = sen2 α
4 sen2 α =3
metr´ II
Trigono-
√
3
sen α = ±
ıa
 2
 √
3 
 α = π + 2k π 2π
 sen α
 = 
 + 2k π
2 3 3
√ =⇒

 sen α 3 
 α = 4π 5π
=− 
 + 2k π + 2k π
2 3 3
Las que no tienen recuadro no cumplen la ecuaci´n inicial.
o
Doc Doc
Volver Cerrar

33. MATEMATICAS
Soluciones a los Ejercicios 33 1º Bachillerato
Ejercicio 6(g)
r=A+lu
A
2 sen(α − 30o ) = − 1 d
1 B
sen(α − 30o ) = − s=B+mv
2 CIENCIAS
α − 30o = 210o + 2kπ 330o + 2kπ
α = 240o + 2k π 330o + 2k π MaTEX
metr´ II
Trigono-
ıa
Doc Doc
Volver Cerrar

34. MATEMATICAS
Soluciones a los Ejercicios 34 1º Bachillerato
Ejercicio 6(h)
r=A+lu
A
sen 2α cosec α = tan α + sec α d
sen α 1 B
2 sen α cos α cosec α = + s=B+mv
cos α cos α CIENCIAS
sen α + 1
2 cos α =
cos α MaTEX
2 cos2 α = sen α + 1
2 (1 − sen2 α) = sen α + 1
metr´ II
Trigono-
2 sen2 α + sen α − 1 =0

1 
 π 5π
ıa
 α =+ 2kπ + 2kπ
sen α = 5 6
2 =⇒
sen α = −1 
 α 3π
 = + 2kπ
2
Las que no tienen recuadro no verifican la ecuaci´n inicial.
o
Doc Doc
Volver Cerrar

35. MATEMATICAS
Soluciones a los Ejercicios 35 1º Bachillerato
Ejercicio 7(a)
r=A+lu
A
2 − sen x = cos2 x + 7 sen2 x d
2 − sen x =1 + 6 sen2 x B
s=B+mv

 sen x = 1
CIENCIAS

6 sen x + sen x − 1 =0 =⇒ 3
2
 sen x = − 1
 MaTEX
2
1 1
sen x = con la calculadora x = arc sen 19,47o
3 3
metr´ II
Trigono-
x = 19,47 + 2 kπ
o
ıa
x = 160,53o + 2 kπ

 x = 7π + 2 kπ


1 
6
sen x = − =⇒
2  x = 11π + 2 kπ



6
Doc Doc
Volver Cerrar

36. MATEMATICAS
Soluciones a los Ejercicios 36 1º Bachillerato
Ejercicio 7(b)
r=A+lu
A
2 sen2 x + 3 cos x =0 d
2 (1 − cos2 x) + 3 cos x =0 B
s=B+mv
CIENCIAS
cos x=2
2 cos x − 3 cos x − 2 =0 =⇒
2
1
cos x = −
2 MaTEX
cos x = 2 no tiene soluci´n pues −1 ≤ cos x ≤ 1
o

 x = 2π + 2 kπ


metr´ II

Trigono-
1 3
cos x = − =⇒
2  x = 4π + 2 kπ


ıa

3
Doc Doc
Volver Cerrar

37. MATEMATICAS
Soluciones a los Ejercicios 37 1º Bachillerato
Ejercicio 7(c)
r=A+lu
A
sen x + cos x =1 d
(sen x − 1)2 = cos2 x B
s=B+mv
CIENCIAS
sen2 x − 2 sen x + 1 = cos2 x
2 sen2 x − 2 sen x =0
MaTEX
sen x = 1
2 sen x(sen x − 1) =0 =⇒
sen x = 0
metr´ II
Trigono-
π
sen x = 1 =⇒ x = + 2 kπ
2
ıa
x = 0 + 2 kπ
sen x = 0 =⇒
x = π + 2 kπ
La que no tiene recuadro no cumple la ecuaci´n inicial. Comprobarlo.
o
Doc Doc
Volver Cerrar

38. MATEMATICAS
Soluciones a los Ejercicios 38 1º Bachillerato
Ejercicio 7(d)
r=A+lu
A
sen2 x + cos x + 1 =0 d
1 − cos2 x + cos x + 1 =0 B
s=B+mv
CIENCIAS
cos x = 2
cos x − cos x − 2 =0 =⇒
2
cos x = −1
cos x = 2 no tiene soluci´n pues −1 ≤ cos x ≤ 1
o
MaTEX
cos x = −1 =⇒ x = π + 2 kπ
metr´ II
Trigono-
ıa
Doc Doc
Volver Cerrar

39. MATEMATICAS
Soluciones a los Ejercicios 39 1º Bachillerato
Ejercicio 7(e)
r=A+lu
A
√
sen x + cos x = 2 d
√
(sen x − 2)2 = cos2 x
B
s=B+mv
√ CIENCIAS
sen2 x − 2 2 sen x + 2 = cos2 x
√
√
2 sen x − 2 2 sen x + 1 =0 =⇒
2
sen x =
2 MaTEX
2

√  x = π + 2 kπ

2 4
metr´ II
Trigono-
sen x = =⇒
2  x = 3π + 2 kπ

4
ıa
La que no tiene recuadro no cumple la ecuaci´n inicial. Comprobarlo.
o
Doc Doc
Volver Cerrar

40. MATEMATICAS
Soluciones a los Ejercicios 40 1º Bachillerato
Ejercicio 7(f )
r=A+lu
A
sen 2x − 2 sen 4x =0 d
sen 2x − 4 sen 2x cos 2x =0 B
s=B+mv
 CIENCIAS
 sen 2x =0
sen 2x(1 − 2 cos 2x) =0 =⇒ 1
 cos 2x =
2
MaTEX
kπ
sen 2x = 0 =⇒ x = 0+
2
metr´ II
Trigono-

 π  x = π + kπ
 2x = + 2 kπ 

ıa
1 3 6
cos 2x = =⇒ =⇒
2  2x = 5π + 2 kπ 
 x = 5π
3  + kπ
6
Doc Doc
Volver Cerrar

41. MATEMATICAS
Soluciones a los Ejercicios 41 1º Bachillerato
Ejercicio 7(g)
r=A+lu
A
2 sen(α − 30o ) = − 1 d
1 B
sen(α − 30o ) = − s=B+mv
2 CIENCIAS
α − 30o = 210o + 2kπ 330o + 2kπ
α = 240o + 2k π 330o + 2k π MaTEX
metr´ II
Trigono-
ıa
Doc Doc
Volver Cerrar

42. MATEMATICAS
Soluciones a los Ejercicios 42 1º Bachillerato
Ejercicio 7(h)
r=A+lu
A
sen 2α cosec α = tan α + sec α d
sen α 1 B
2 sen α cos α cosec α = + s=B+mv
cos α cos α CIENCIAS
sen α + 1
2 cos α =
cos α MaTEX
2 cos2 α = sen α + 1
2 (1 − sen2 α) = sen α + 1
metr´ II
Trigono-
2 sen2 α + sen α − 1 =0


 α π 5π
ıa
1 
 = + 2kπ + 2kπ
sen α = 5 6
2 =⇒
sen α = −1 
 α 3π

 = + 2kπ
2
Doc Doc
Volver Cerrar

43. MATEMATICAS
Soluciones a los Ejercicios 43 1º Bachillerato
Ejercicio 8(a)
r=A+lu
A
1 − cos 2 α 1 − cos2 α + sen2 α
= cos 2α
d
cos2 α cos2 α B
s=B+mv
2 sen2 α CIENCIAS
= for. fundamental
cos2 α
=2 tan2 α
MaTEX
metr´ II
Trigono-
ıa
Doc Doc
Volver Cerrar

44. MATEMATICAS
Soluciones a los Ejercicios 44 1º Bachillerato
Ejercicio 8(b)
r=A+lu
A
1 + cos 2 α 1 + cos2 α − sen2 α
= cos 2α
d
cos2 α cos2 α B
s=B+mv
2 cos2 α CIENCIAS
= for. fundamental
cos2 α
=2 MaTEX
metr´ II
Trigono-
ıa
Doc Doc
Volver Cerrar

45. MATEMATICAS
Soluciones a los Ejercicios 45 1º Bachillerato
Ejercicio 8(c)
r=A+lu
A
1 − cos 2 α 1 − cos2 α + sen2 α
= cos 2α
d
sen2 α sen2 α B
s=B+mv
2 sen2 α CIENCIAS
= for. fundamental
sen2 α
=2 MaTEX
metr´ II
Trigono-
ıa
Doc Doc
Volver Cerrar

46. MATEMATICAS
Soluciones a los Ejercicios 46 1º Bachillerato
Ejercicio 8(d)
r=A+lu
A
cos 2 α cos2 α − sen2 α
= cos 2α
d
cos α − sen α cos α − sen α B
s=B+mv
(cos α − sen α)(cos α + sen α)
CIENCIAS
= dif. cuadrados
cos α − sen α
= cos α + sen α
MaTEX
metr´ II
Trigono-
ıa
Doc Doc
Volver Cerrar

47. MATEMATICAS
Soluciones a los Ejercicios 47 1º Bachillerato
Ejercicio 9(a) Sumando las expresiones:
r=A+lu
A
sen(45 + β) = sen 45 cos β + cos 45 sen β d
B
cos(45 + β) = cos 45 cos β − sen 45 sen β s=B+mv
CIENCIAS
se obtiene √
sen(45 + β) + cos(45 + β) = 2 cos β
MaTEX
metr´ II
Trigono-
ıa
Doc Doc
Volver Cerrar

48. MATEMATICAS
Soluciones a los Ejercicios 48 1º Bachillerato
Ejercicio 9(b) Sumando las expresiones:
r=A+lu
A
sen(30 + β) = sen 30 cos β + cos 30 sen β d
√ B
1 3 s=B+mv
= cos β + sen β CIENCIAS
2 2
cos(60 + β) = cos 60 cos β − sen 60 sen β MaTEX
√
1 3
= cos β − sen β
2 2
metr´ II
Trigono-
se obtiene
sen(30 + β) + cos(60 + β) = cos β
ıa
Doc Doc
Volver Cerrar

49. MATEMATICAS
Soluciones a los Ejercicios 49 1º Bachillerato
Ejercicio 9(c) Sumando las expresiones:
r=A+lu
A
sen(30 + x) = sen 30 cos x + cos 30 sen x d
√ B
1 3 s=B+mv
= cos x + sen x CIENCIAS
2 2
sen(30 − x) = sen 30 cos x − cos 30 sen x MaTEX
√
1 3
= cos x − sen x
2 2
metr´ II
Trigono-
se obtiene
sen(30 + x) + sen(30 − x) = cos x
ıa
Doc Doc
Volver Cerrar

50. MATEMATICAS
Soluciones a los Ejercicios 50 1º Bachillerato
Ejercicio 9(d) Restando las expresiones:
r=A+lu
A
cos(30 + x) = cos 30 cos x − sen 30 sen x d
√ B
3 1 s=B+mv
= cos x − sen x CIENCIAS
2 2
cos(30 − x) = cos 30 cos x + sen 30 sen x MaTEX
√
3 1
= cos x + sen x
2 2
metr´ II
Trigono-
se obtiene
cos(30 + x) − cos(30 − x) = − sen x
ıa
Doc Doc
Volver Cerrar

51. MATEMATICAS
Soluciones a los Ejercicios 51 1º Bachillerato
Ejercicio 10. Quitamos denominadores:
r=A+lu
A
sen 3x cos x − cos 3x sen x = 2 sen x cos x d
En el miembro de la izquierda convertimos los productos en sumas
B
s=B+mv
CIENCIAS
1
sen 3x cos x = (sen 4x + sen 2x)
2
1
MaTEX
cos 3x sen x = (sen 4x − sen 2x)
2
y restando se obtiene
metr´ II
Trigono-
sen 3x cos x − cos 3x sen x = sen 2x = 2 sen x cos x
Ejercicio 10
ıa
Doc Doc
Volver Cerrar

52. MATEMATICAS
Soluciones a los Ejercicios 52 1º Bachillerato
Ejercicio 11. De la tangente del ´ngulo doble se tiene
a
r=A+lu
A
2 tan α
tan 2α = (haciendo tan α = a) d
1 − tan2 α B
2 2a
s=B+mv
= (operando) CIENCIAS
3 1 − a2
0 =2a2 + 6a − 2
√
(resolviendo) MaTEX
−3 ± 13
a = tan α = (α ∈ 3o cuadrante)
2√
−3 + 13
metr´ II
Trigono-
tan α =
2
Ejercicio 11
ıa
Doc Doc
Volver Cerrar

53. MATEMATICAS
Soluciones a los Ejercicios 53 1º Bachillerato
Ejercicio 12. Planteamos el problema como una ecuaci´n. Sea α el ´ngulo
o a
r=A+lu
A
buscado, entonces
d
tan α = cot α B
s=B+mv
1 CIENCIAS
tan α =
tan α
tan2 α =1 MaTEX
tan α = ± 1
α = 45o , 135o , 225o , 315o
metr´ II
Trigono-
Ejercicio 12
ıa
Doc Doc
Volver Cerrar