Este documento presenta conceptos básicos sobre variables aleatorias discretas. En 3 oraciones: Introduce variables aleatorias discretas como funciones que asignan valores numéricos a resultados de experimentos aleatorios. Explica que la función de probabilidad asigna a cada valor de la variable aleatoria la probabilidad de que tome ese valor, de modo que la suma de las probabilidades sea 1. Presenta ejemplos como lanzar monedas para ilustrar variables aleatorias y sus funciones de probabilidad.

1. MATEMATICAS
2º Bachillerato
MaTEX
r=A+lu
Proyecto A
d
B
s=B+mv
Variables Aleatorias SOCIALES
MaTEX
Aleatorias
Fco Javier Gonz´lez Ortiz
a
Variables
Directorio
• Tabla de Contenido
• Inicio Art´
ıculo
Tabla N(0,1)
c 2004 gonzaleof@unican.es Doc Doc
8 de Junio de 2004 Versi´n 1
o
Volver Cerrar

2. MATEMATICAS
2º Bachillerato
Tabla de Contenido A
r=A+lu
1. Variable Aleatoria Discreta d
1.1. Funci´n de Probabilidad
o B
s=B+mv
1.2. Funci´n de Distribuci´n
o o SOCIALES
1.3. Media o esperanza de una variable aleatoria
1.4. Varianza y desviaci´n t´
o ıpica de una variable aleatoria MaTEX
1.5. Ejercicios
Aleatorias
2. La Distribuci´n Binomial
o
Variables
• Experiencias binomiales • N´meros combinatorios
u
2.1. Distribuci´n Binomial
o
2.2. Ejercicios
3. Variable Aleatoria Continua
3.1. Funci´n de Distribuci´n
o o
4. La Distribuci´n Normal
o
4.1. La normal N (0; 1)
• Manejo de la tabla • Tipificar una variable normal
4.2. Ejercicios
Tabla N(0,1)
5. Aproximaci´n de la distribuci´n binomial por la normal
o o
5.1. Ejercicios
Soluciones a los Ejercicios
Soluciones a los Tests Doc Doc
Volver Cerrar

3. MATEMATICAS
Secci´n 1: Variable Aleatoria Discreta
o 3 2º Bachillerato
r=A+lu
1. Variable Aleatoria Discreta A
Definici´n 1.1 Una variable aleatoria discreta X es una funci´n que asigna
o o d
valores num´ricos a los sucesos elementales de un espacio muestral
e B
s=B+mv
X : Ω −→ R SOCIALES
ωi −→ xi
Ejemplo 1.1. Lanzamos dos monedas y definimos la variable aleatoria X,
MaTEX
Aleatorias
n´mero de caras obtenidas. Siendo C obtener cara y X obtener cruz, como
u
el espacio muestral es Ω = {CC, CX, XC, XX} entonces se tiene
Variables
X : Ω −→ R
CC → 2
CX → 1
XC → 1
XX → 0
Ejemplo 1.2. Lanzamos una moneda, si sacamos cara C recibimos 1 euro y
si sacamos cruz X pagamos 1 euro. ¿ C´mo es la variable aleatoria X que
o
mide la ganancia?.
Tabla N(0,1)
El espacio muestral es Ω = {C, X} entonces se tiene
X : Ω −→ R
C → 1
X → −1 Doc Doc
Volver Cerrar

4. MATEMATICAS
Secci´n 1: Variable Aleatoria Discreta
o 4 2º Bachillerato
r=A+lu
1.1. Funci´n de Probabilidad
o A
Definici´n 1.2 Es la aplicaci´n que asigna a cada valor de la variable aleato-
o o d
ria discreta X la probabilidad de que la variable tome dicho valor B
s=B+mv
px : X −→ [0, 1] SOCIALES
xi −→ P (X = xi )
Ejemplo 1.3. Lanzamos dos monedas y definimos la variable aleatoria X,
MaTEX
Aleatorias
n´mero de caras obtenidas. Siendo C obtener cara y X obtener cruz. La
u
funci´n de probabilidad de X es
o
Variables
1
px (2) = P (X = 2) = P (“CC ) =
4
2
px (1) = P (X = 1) = P (“CX, XC ) =
4
1
px (0) = P (X = 0) = P (“XX ) =
4
Es habitual expresar la funci´n de probabilidad en una tabla de la forma
o
xi 0 1 2
1 2 1
px (xi ) Tabla N(0,1)
4 4 4
Observa que se tiene que cumplir
n
px (xi ) = 1 (1) Doc Doc
i=1
Volver Cerrar

5. MATEMATICAS
Secci´n 1: Variable Aleatoria Discreta
o 5 2º Bachillerato
r=A+lu
Ejemplo 1.4. Lanzamos una moneda, si sacamos cara C recibimos 1 euro y A
si sacamos crus X pagamos 1 euro. Describir la funci´n de probabilidad de
o
d
la variable aleatoria X que mide la ganancia. B
xi 1 −1 s=B+mv
SOCIALES
px (xi ) 1/2 1/2
Ejemplo 1.5. La funci´n de probabilidad de la variable aleatoria X viene
o
MaTEX
Aleatorias
dada por la tabla.
Variables
xi −2 −1 0 1 2
px (xi ) 0.08 0.32 0.05 a 0.32
Hallar el valor de a, P (X = 1), P (X ≥ 1) y P (X ≤ −1).
Soluci´n:
o
n
• Como px (xi ) = 1 ⇒ 0.08 + 0.32 + 0.05 + a + 0.32 = 1; a = 0.23
i=1
• P (X = 1) = px (1) = a = 0.23
• P (X ≥ 1) = P (X = 1) + P (X = 2) = 0.23 + 0.32 = 0.55 Tabla N(0,1)
• P (X ≤ −1) = P (X = −2) + P (X = −1) = 0.08 + 0.32 = 0.4
Doc Doc
Volver Cerrar

6. MATEMATICAS
Secci´n 1: Variable Aleatoria Discreta
o 6 2º Bachillerato
r=A+lu
1.2. Funci´n de Distribuci´n
o o A
Definici´n 1.3 Es la aplicaci´n FX (xi ) que asigna a cada valor xi de la
o o d
variable aleatoria discreta X la probabilidad de que la variable tome valores B
s=B+mv
menores o iguales que xi SOCIALES
FX (xi ) = P (X ≤ xi ) (2)
MaTEX
Ejemplo 1.6. La funci´n de probabilidad de la variable aleatoria X viene
o
Aleatorias
dada por la tabla.
Variables
xi 0 1 2 3
px (xi ) 0.1 0.2 0.4 0.3
Hallar la funci´n de distribuci´n de X.
o o
Soluci´n: De la definici´n (1.3) se tiene
o o
FX (0) = P (X ≤ 0) = px (0) = 0.1
FX (1) = P (X ≤ 1) = px (0) + px (1) = 0.3
FX (2) = P (X ≤ 2) = px (0) + px (1) + px (2) = 0.7
FX (3) = P (X ≤ 1) = px (0) + px (1) + px (2) + px (3) = 1
Tabla N(0,1)
xi 0 1 2 3
Fx (xi ) 0.1 0.3 0.7 1
Doc Doc
Volver Cerrar

7. MATEMATICAS
Secci´n 1: Variable Aleatoria Discreta
o 7 2º Bachillerato
r=A+lu
Ejemplo 1.7. La funci´n de probabilidad de la variable aleatoria X viene
o A
dada por la tabla.
d
xi 0 1 2 3 B
s=B+mv
px (xi ) 0.2 0.3 0.1 0.5 SOCIALES
Representar la funci´n de probabilidad y la funci´n de distribuci´n de X
o o o MaTEX
Soluci´n: Juntamos en una tabla la funci´n de probabilidad y la funci´n de
o o o
Aleatorias
distribuci´n de X
o
Variables
xi 0 1 2 3
px (xi ) 0.2 0.3 0.1 0.4
FX (xi ) 0.2 0.5 0.6 1
p(x) F(x)
1 1
0.6 0.6
0.5 0.5
0.4 0.4
0.3 0.3 Tabla N(0,1)
0.2 0.2
0.1 0.1
0 1 2 3 X 0 1 2 3 X
Doc Doc
Volver Cerrar

8. MATEMATICAS
Secci´n 1: Variable Aleatoria Discreta
o 8 2º Bachillerato
r=A+lu
1.3. Media o esperanza de una variable aleatoria A
Definici´n 1.4 Se llama media o esperanza de una variable aleatoria X y
o d
se representa por µ al valor B
s=B+mv
n SOCIALES
µ = x1 · p(x1 ) + x2 · p(x2 ) + · · · xn · p(xn ) = xi · p(xi ) (3)
i=1 MaTEX
Aleatorias
Ejemplo 1.8. Lanzamos dos monedas. Si salen dos caras recibimos 3 eu-
Variables
ros, si sale una cara recibimos 1 euro y si no sale ninguna cara pagamos 5
euros.¿Cu´l es la ganancia media del juego?
a
Soluci´n: Hallamos la funci´n de probabilidad de la ganancia X en euros:
o o
xi 3 1 −5
px (xi ) 1/4 1/2 1/4
La ganancia media del juego es la media o esperanza de X
µ =x1 · p(x1 ) + x2 · p(x2 ) + x3 · p(x3 )
1 1 1
=3 · + 1 · − 5 · = 0
4 2 4 Tabla N(0,1)
Cuando en un juego la ganancia esperada µ = 0 se llama juego justo. Si
µ > 0 es un juego con ventaja y si µ < 0 es un juego en desventaja.
Doc Doc
Volver Cerrar

9. MATEMATICAS
Secci´n 1: Variable Aleatoria Discreta
o 9 2º Bachillerato
r=A+lu
Ejemplo 1.9. Hallar la media de la variable aleatoria X, dada por la funci´n
o A
de probabilidad.
d
xi 0 1 2 3 B
s=B+mv
px (xi ) 0.1 0.2 0.4 0.3 SOCIALES
Soluci´n: De la definici´n (1.4) se tiene
o o
MaTEX
µ =x1 · p(x1 ) + x2 · p(x2 ) + x3 · p(x3 ) + x4 · p(x4 )
Aleatorias
=0 · 0.1 + 1 · 0.2 + 2 · 0.4 + 3 · 0.3 = 1.9
Variables
Ejemplo 1.10. Hallar la media de la variable aleatoria X, dada por la
funci´n de probabilidad.
o
xi 0 1 2 3
px (xi ) 0.3 0.2 0.1 0.4
Soluci´n: De la definici´n (1.4) se tiene
o o
µ =x1 · p(x1 ) + x2 · p(x2 ) + x3 · p(x3 ) + x4 · p(x4 )
Tabla N(0,1)
=0 · 0.3 + 1 · 0.2 + 2 · 0.1 + 3 · 0.4 = 1.6
Doc Doc
Volver Cerrar

10. MATEMATICAS
Secci´n 1: Variable Aleatoria Discreta
o 10 2º Bachillerato
r=A+lu
1.4. Varianza y desviaci´n t´
o ıpica de una variable aleatoria A
Definici´n 1.5 Se llama varianza de una variable aleatoria X y se repre-
o d
senta por σ 2 al valor B
s=B+mv
n SOCIALES
σ 2 = x2 · p(x1 ) + x2 · p(x2 ) + · · · x2 · p(xn ) − µ2 = x2 · p(xi ) − µ2 (4)
1 2 n
i=1
i
MaTEX
Aleatorias
A partir de la varianza se define la desviaci´n t´
o ıpica σ como la ra´ cuadrada
ız
de la varianza.
Variables
Ejemplo 1.11. Hallar la varianza y la desviaci´n t´
o ıpica de la variable aleato-
ria X, dada por la funci´n de probabilidad.
o
xi 0 1 2 3
px (xi ) 0.1 0.2 0.4 0.3
Soluci´n: Primero se calcula la media µ
o
µ =0 · 0.1 + 1 · 0.2 + 2 · 0.4 + 3 · 0.3 = 1.9
De la definici´n (1.5) se tiene
o
σ 2 =x2 · p(x1 ) + x2 · p(x2 ) + · · · x2 · p(xn ) − µ2
1 2 n
Tabla N(0,1)
=02 · 0.1 + 12 · 0.2 + 22 · 0.4 + 32 · 0.3 − 1.92 = 0.89
√
σ = 0.89 = 0.94
Doc Doc
Volver Cerrar

11. MATEMATICAS
Secci´n 1: Variable Aleatoria Discreta
o 11 2º Bachillerato
r=A+lu
1.5. Ejercicios A
Ejercicio 1. La funci´n de probabilidad de una variable aleatoria discreta
o d
X es. B
s=B+mv
xi 0 1 2 3 4 SOCIALES
px (xi ) 0.1 a b c 0.2
MaTEX
Sabiendo que P (X ≤ 2) = 0.75 y que P (X ≥ 2) = 0.75, halla su esperanza
Aleatorias
matem´tica y su desviaci´n t´
a o ıpica.
Variables
Ejercicio 2. Una persona en un juego recibe 15 cts cuando saca una sota
o un caballo y recibe 5 cts si saca un rey o un as de una baraja espa˜ola
n
de 40 cartas. Si saca cualquier otra carta paga 4 cts . ¿Cu´l es la ganancia
a
esperada en este juego?
Ejercicio 3. Se tienen tres urnas: la A que contiene dos bolas negras y cuatro
rojas, la B tres negras y tres rojas; y la C con una negra y cinco rojas.
UA = {2 N ; 4 R} UB = {3 N ; 3 R} UC = {1 N ; 5 R}
Se elige una urna al azar y se extrae una bola de ella. Si se saca roja se
Tabla N(0,1)
reciben 3 euros y si se saca negra no se recibe nada. ¿Cu´l es la ganancia
a
esperada?
Doc Doc
Volver Cerrar

12. MATEMATICAS
Secci´n 2: La Distribuci´n Binomial
o o 12 2º Bachillerato
r=A+lu
2. La Distribuci´n Binomial
o A
• Experiencias binomiales d
Toda experiencia aleatoria que presenta dos resultados posibles, uno que fi- B
s=B+mv
jamos como “´xito” y lo contrario como “fracaso” se suele denominar de tipo
e SOCIALES
Bernouilli.
Por ejemplo las siguientes experiencias son de tipo Bernouilli: MaTEX
• Jugar a cara o cruz.
Aleatorias
• El nacimiento de un ni˜o (var´n o mujer)
n o
Variables
• Obtener un “4” en el lanzamiento de un dado.
• Obtener un n´mero “par” en el lanzamiento de un dado.
u
• Obtener “copas” al extraer una carta de la baraja espa˜ola.
n
• La fabricaci´n de una pieza en un factor´ (aceptable o defectuosa).
o ıa
• El resultado de una operaci´n (´xito o fracaso).
o e
• El lanzamiento a una canasta (encestar o fallar).
• Aprobar o suspender un examen.
Tabla N(0,1)
Doc Doc
Volver Cerrar

13. MATEMATICAS
Secci´n 2: La Distribuci´n Binomial
o o 13 2º Bachillerato
r=A+lu
Cuando se realizan n pruebas independientes de tipo Bernouilli decimos A
que es una experiencia aleatoria de tipo Binomial.
d
B
Por ejemplo las siguientes experiencias son de tipo Binomial: s=B+mv
SOCIALES
• Jugar 10 veces a cara o cruz .
• Observar 30 nacimientos de un beb´ (ni˜a o ni˜o)
e n n MaTEX
• Obtener el “4” en el lanzamiento de 15 dados.
Aleatorias
• Obtener “copas” al extraer una carta 8 veces de la baraja espa˜ola.
Variables
n
• La fabricaci´n de 1000 piezas en un factor´ (aceptable o defectuosa).
o ıa
• El resultado de 50 operaciones (´xito o fracaso).
e
• El lanzamiento a una canasta n veces (encestar o fallar).
Tabla N(0,1)
Doc Doc
Volver Cerrar

14. MATEMATICAS
Secci´n 2: La Distribuci´n Binomial
o o 14 2º Bachillerato
r=A+lu
• N´meros combinatorios
u A
Lanzamos una moneda 5 veces. Sea el suceso C =“sacar cara” como “´xito”,y
e d
el suceso contrario X como “fracaso”. B
¿ De cu´ntas formas se puede presentar el suceso “sacar dos caras”?
a s=B+mv
SOCIALES
Es como colocar dos C en 5 casillas. La primera C dispone de 5 sitios,
luego la segunda dispone de 4 sitios. Eso har´ 5 · 4 = 20 posibilidades. Pero
ıa
5·4
MaTEX
como las caras C son indistinguibles dividimos por 2. Eso hace = 10.
Aleatorias
2
en efecto
Variables

CCXXX XCXCX  
CXCXX XCXXC 

5·4 5
CXXCX XXCCX = = 10
 2 2
CXXXC XXCXC  

XCCXX XXXCC

5
El n´mero combinatorio
u se lee 5 sobre 2 y se calcula de la forma siguiente:
2
5 5·4
= = 10 Tabla N(0,1)
2 2·1
Las formas de obtener 3 caras en los cinco lanzamientos corresponde de forma
a an´loga a
a
5 5·4·3 Doc Doc
= = 10
3 3·2·1
Volver Cerrar

15. MATEMATICAS
Secci´n 2: La Distribuci´n Binomial
o o 15 2º Bachillerato
r=A+lu
Las formas de obtener 4 caras en seis lanzamientos de una moneda ser´
ıa A
6 6·5·4·3
= = 15 d
4 4·3·2·1 B
s=B+mv
Las formas de aparecer 5 defectuosas en 40 piezas fabricadas ser´
ıa SOCIALES
40
5
=
40 · 39 · 38 · 37 · 36
5·4·3·2·1
= 658008 MaTEX
Aleatorias
En general las formas de obtener k ´xitos en n intentos corresponde a
e
Variables
n n · (n − 1) · · · (n − k + 1)
= (5)
k k!
Para extender la f´rmula anterior se toma 0! = 1.
o
Ejercicio 4. Calcula los siguientes n´mero combinatorios
u
Tabla N(0,1)
4 6 8 10
a) b) c) d)
1 2 3 2
5 7 9 13
e) f) g) h)
0 3 4 2 Doc Doc
Volver Cerrar

16. MATEMATICAS
Secci´n 2: La Distribuci´n Binomial
o o 16 2º Bachillerato
r=A+lu
Ejemplo 2.1. En el lanzamiento de un dado Considera como “´xito” ele A
suceso E =“sacar un 4” y como fracaso el suceso contrario F con p = P (E) =
d
1 5
y q = P (F ) = . Queremos hallar la probabilidad de obtener un ´xito en
e B
6 6 s=B+mv
tres dados. Esto puede ocurrir como se muestra en la tabla SOCIALES
Dado 1 Dado 2 Dado 3 Probabilidad MaTEX
1 5 5
E F F · · = p q2
Aleatorias
6 6 6
Variables
5 1 5
F E F · · = p q2
6 6 6
5 5 1
F F E · · = p q2
6 6 6
3 p q2
3
Como hay formas distintas,la probabilidad de obtener un ´xito en tres
e
1
intentos es:
3
P (X = 1) = p q2
1
Tabla N(0,1)
Si generalizamos el ejemplo anterior obtenemos la distribuci´n bimomial.
o
Doc Doc
Volver Cerrar

17. MATEMATICAS
Secci´n 2: La Distribuci´n Binomial
o o 17 2º Bachillerato
r=A+lu
2.1. Distribuci´n Binomial
o A
Definici´n 2.1 Una variable aleatoria X se llama binomial si su valor en
o d
igual al n´mero de ´xitos que ocurren en n pruebas independientes,teniendo
u e B
s=B+mv
todas ellas la misma probabilidad de ´xito, que designamos por p. Su funci´n
e o SOCIALES
de probabilidad es
n k n−k
MaTEX
P (X = k) = p (1 − p) , para k = 0, 1, . . . , n; (6)
Aleatorias
k
Variables
Si una variable X sigue la distribuci´n binomial de par´metros n y p suele
o a
designarse como
X ∼ B(n; p)
Las constantes n y p son los par´metros de la distribuci´n; obviamente, n 0
a o
es un n´mero entero y 0 ≤ p ≤ 1. La probabilidad de obtener fracaso es 1 − p
u
y se designa con al letra q de forma que p + q = 1.
El c´lculo de la media , la varianza y la desviaci´n t´
a o ıpica es algo laborioso
y resulta
Tabla N(0,1)
µ = n·p
σ2 = n · p · q (7)
√
σ = n·p·q
Doc Doc
Volver Cerrar

18. MATEMATICAS
Secci´n 2: La Distribuci´n Binomial
o o 18 2º Bachillerato
r=A+lu
Ejemplo 2.2. Tiramos una moneda 6 veces y contamos el n´mero de caras
u A
X. Hallar la funci´n de probabilidad y representarla.
o
d
Soluci´n: Se tiene que
o B
s=B+mv
SOCIALES
0.35
X es B(n = 6; p = 1/2)
p(X=k)
6
0.3
MaTEX
P (X = 0) = p0 q 6 = 0.0156 0.25
Aleatorias
0
0.2
Variables
6
P (X = 1) = p1 q 5 = 0.0938
1 0.15
6 0.1
P (X = 2) = p2 q 4 = 0.2344
2 0.05
6 3 3 0
P (X = 3) = p q = 0.3125 0 1 2 3 4 5 6
3 Nº de caras
6
P (X = 4) = p4 q 2 = 0.2344
4 1
µ = np = 10 =5
6 2
P (X = 5) = p5 q 1 = 0.0938 11
Tabla N(0,1)
5 σ 2 = npq = 10 = 2.5
6 22
P (X = 6) = p6 q 0 = 0.0156
6
Doc Doc
Volver Cerrar

19. MATEMATICAS
Secci´n 2: La Distribuci´n Binomial
o o 19 2º Bachillerato
r=A+lu
Ejemplo 2.3. Se extraen cinco bolas con reemplazamiento de una urna que A
tiene 6 bolas blancas y 8 negras. ¿Qu´ es mas probable, sacar 2 rojas o 3
e
d
rojas?. B
s=B+mv
Soluci´n: Sea ´xito sacar roja, con p = 6/14,
o e SOCIALES
Se tiene que
6
0.35
0.3
p(X=k) MaTEX
X es B(n = 5; p = )
Aleatorias
14 0.25
Variables
Probabilidad de sacar 2 bolas ro-
0.2
jas:
2 3 0.15
5 6 8
P (X = 2) =
2 14 14 0.1
= 0.3427 0.05
Probabilidad de sacar 3 bolas ro- 0 1 2 3 4 5
jas: Nº de bolas rojas
3 2
5 6 8
P (X = 3) = Tabla N(0,1)
3 14 14
= 0.2570
Es m´s probable obtener 2 rojas.
a
Doc Doc
Volver Cerrar

20. MATEMATICAS
Secci´n 2: La Distribuci´n Binomial
o o 20 2º Bachillerato
r=A+lu
2.2. Ejercicios A
Ejercicio 5. La probabilidad de que cierto jugador de baloncesto enceste d
una canasta de 3 puntos es 0.3. ¿Cu´l es la probabilidad de que enceste,
a B
s=B+mv
exactamente dos canastas de cinco lanzamientos? SOCIALES
Ejercicio 6. La probabilidad de que un estudiante que ingresa en la Univer-
sidad se licencie en 5 a˜os es de 0.4. Se eligen al azar 10 estudiantes. Calcular
n
MaTEX
Aleatorias
la probabilidad de que:
Variables
a) ninguno se licencie en 5 a˜os.
n
b) todos se licencien en 5 a˜os.
n
c) un unico estudiante se licencie en 5 a˜os.
´ n
Ejercicio 7. Una m´quina produce 12 piezas defectuosas de cada mil que
a
fabrica. Hallar la probabilidad de que al examinar 40 piezas::
a) s´lo haya una defectuosa.
o
b) no haya ninguna defectuosa.
Ejercicio 8. En un grupo de 20 estudiantes de un instituto se ha comprobado Tabla N(0,1)
que cada alumno falta a clase el 4% de los d´
ıas. Calcular la probabilidad de
que en un d´ determinado:
ıa
a) no se registre ninguna falta.
b) falten a clase menos de tres estudiantes. Doc Doc
Volver Cerrar

21. MATEMATICAS
Secci´n 2: La Distribuci´n Binomial
o o 21 2º Bachillerato
r=A+lu
c) falte a clase un unico estudiante.
´ A
Ejercicio 9. En una determinada ciudad, la probabilidad del nacimiento de d
una ni˜a es del 56%. Seleccionamos una familia de cinco hijos. Calcular la
n B
s=B+mv
probabilidad de que SOCIALES
a) tenga exactamente tres ni˜as.
b) tenga al menos dos ni˜as.
n
n
MaTEX
Aleatorias
c) ¿cu´l es el n´mero medio de hijas en las familias con cinco hijos?
a u
Variables
Ejercicio 10. A una fiesta han sido invitadas 8 personas. Cada persona
puede acudir o no con independencia de que lo hagan las dem´s. Si la prob-
a
abilidad de que acuda cada una es 0.85, calcular:
a) la probabilidad de asistan todas.
b) la probabilidad de asistan m´s de 6 personas.
a
c) la probabilidad de asista al menos la mitad.
Ejercicio 11. Si el 20% de las piezas producidas por una m´quina son defec-
a
tuosas, ¿cu´l es la probabilidad de que entre cuatro piezas elegidas al azar, a
a Tabla N(0,1)
lo sumo 2 sean defectuosas?
Ejercicio 12. La probabilidad de que un esquiador debutante se caiga en la
pista es 0,4. Si lo intenta 5 veces, calcula la probabilidad de que se caiga al
menos 3 veces. Doc Doc
Volver Cerrar

22. MATEMATICAS
Secci´n 3: Variable Aleatoria Continua
o 22 2º Bachillerato
r=A+lu
3. Variable Aleatoria Continua A
Diremos que una variable aleatoria es continua cuando puede tomar cualquier d
valor en un intervalo. Por ejemplo, el peso o la altura de una persona. Para B
s=B+mv
concretar, consideremos que representamos en un histograma las medida de SOCIALES
la alturas X de los chicos de 15 a˜os. Si tomamos m´s y m´s observaciones
n a a
y haciendo clases cada vez m´s finas, el histograma tender´ a una curva
a a MaTEX
que describir´ el comportamiento de la variable estudiada, como muestra la
a
Aleatorias
figura.
Variables
Eso hace pensar en una funci´n matem´tica f (x) que modelice la frecuen-
o a
cia relativa de la altura para la poblaci´n de los chicos de 15 a˜os.
o n
A dicha funci´n f (x) se le llama funci´n de densidad.
o o
y
f (x)
Tabla N(0,1)
1.53 1.83 x
altura Doc Doc
Volver Cerrar

23. MATEMATICAS
Secci´n 3: Variable Aleatoria Continua
o 23 2º Bachillerato
r=A+lu
Definici´n 3.1 Una variable aleatoria X se dice que es continua cuando
o A
tiene asociada una funci´n de densidad f (x) que cumple
o
d
1. f (x) ≥ 0 para todos los valores donde est´ definida.
a B
s=B+mv
∞
SOCIALES
2. f (x) dx = 1. (El ´rea bajo la curva es uno)
a
−∞
La probabilidad se determina con MaTEX
Aleatorias
b
P (a x b) = f (x) dx (8)
Variables
a
que corresponde al ´rea de la regi´n limitada por f (x), el eje x y las rectas
a o
x=ayx=b
y
f (x)
Tabla N(0,1)
a b x
P (a x b) Doc Doc
Volver Cerrar

24. MATEMATICAS
Secci´n 3: Variable Aleatoria Continua
o 24 2º Bachillerato
r=A+lu
3.1. Funci´n de Distribuci´n
o o A
Definici´n 3.2 Es la aplicaci´n FX (x) que asigna a cada valor x de la vari-
o o d
able aleatoria continua X la probabilidad de que la variable tome valores B
s=B+mv
menores o iguales que x SOCIALES
FX (x) = P (X ≤ x) (9)
MaTEX
Ejemplo 3.1. Hallar la funci´n de distribuci´n de la variable aleatoria con-
o o
Aleatorias
tinua X que tiene por funci´n de densidad.
o
Variables
2x 0 x 1
f (x) =
0 en el resto
Soluci´n: De la definici´n (9) se tiene
o o
x f(x)
F (x) =P (X ≤ x) = 2x dx 2
0
x · 2x
=´rea del tri´ngulo gris =
a a = x2 2x
2
F (x) = x2 0x1 Tabla N(0,1)
x 1 X
Doc Doc
Volver Cerrar

25. MATEMATICAS
Secci´n 3: Variable Aleatoria Continua
o 25 2º Bachillerato
r=A+lu
Ejemplo 3.2. La variable aleatoria X del ejemplo anterior tiene como funci´n
o A
de distribuci´n
o
d
F (x) = x2 0x1 B
s=B+mv
Hallar las siguientes probabilidades: SOCIALES
a) P (x 0.5) b) P (x 0.2) c) P (0.2 x 0.5)
d ) P (x 0.5) e) P (x 0.2) f ) P (0.1 x 0.8) MaTEX
Aleatorias
Soluci´n:
o
Variables
a) P (x 0.5) = F (0.5) = 0.52 = 0.25
b) P (x 0.2) = F (0.2) = 0.22 = 0.04
c) P (0.2 x 0.5) = F (0.5) − F (0.2) = 0.25 − 0.04 = 0.21
d ) P (x 0.5) = 1 − F (0.5) = 1 − 0.25 = 0.75
e) P (x 0.2) = 1 − F (0.2) = 1 − 0.04 = 0.96
f ) P (0.1 x 0.8) = F (0.8) − F (0.1) = 0.64 − 0.01 = 0.63
Para hallar P (a x ≤ b) utilizamos la expresi´n:
o Tabla N(0,1)
P (a x ≤ b) = FX (b) − FX (a) (10)
Doc Doc
Volver Cerrar

26. MATEMATICAS
Secci´n 4: La Distribuci´n Normal
o o 26 2º Bachillerato
r=A+lu
4. La Distribuci´n Normal
o A
La funci´n de distribuci´n normal juega un papel central en la estad´
o o ıstica ya d
que, adem´s de sus interesantes propiedades de reproductividad y de aprox-
a B
s=B+mv
imaci´n de otras distribuciones, sirve para modelizar una gran cantidad de
o SOCIALES
situaciones pr´cticas.
a
Definici´n 4.1 Distribuci´n Normal. Una variable aleatoria X se dice
o o MaTEX
que tiene una distribuci´n de probabilidades normal con media µ y varianza
o
Aleatorias
σ 2 y se denomina N (µ, σ 2 ) si su funci´n de densidad es de la forma:
o
Variables
(x − µ)2
1 −
f (x) = √ e 2σ 2 , −∞ x ∞.
σ 2π
La media y varianza de una variable normal coinciden con los par´metros µ
a
y σ 2 de la misma.
En la figura se muestra la
funci´n de densidad y se
o
aprecia que es sim´trica re-
e
specto de x = µ y los Tabla N(0,1)
puntos de inflexi´n de la
o
funci´n de densidad se en-
o
cuentran a una distancia σ µ−σ µ µ+σ z
de la media.
Doc Doc
Volver Cerrar

27. MATEMATICAS
Secci´n 4: La Distribuci´n Normal
o o 27 2º Bachillerato
r=A+lu
En la figura se muestran dos distribuciones normales, con media µ = 0 y A
desviaciones t´
ıpicas σ = 1 y σ = 0.5. Como las dos tienen la misma media
d
µ = 0, la funci´n roja es mas alargada pues tiene menos variabilidad que la
o B
azul. s=B+mv
SOCIALES
MaTEX
Aleatorias
Variables
Tabla N(0,1)
-3 -2 -1 0 1 2 3 Doc Doc
Volver Cerrar

28. MATEMATICAS
Secci´n 4: La Distribuci´n Normal
o o 28 2º Bachillerato
r=A+lu
4.1. La normal N (0; 1) A
Primero estudiaremos la normal t´ ıpica, que tiene media µ = 0 y desviaci´n
o d
t´
ıpica σ = 1, N (0; 1) y se designa con la letra z. B
s=B+mv
SOCIALES
Para calcular las probabilidades
P (Z ≤ z0 ) = Φ(z0 ) MaTEX
se dise˜a una tabla que pro-
n Φ(z0 )
Aleatorias
porciona las respectivas probabil-
Variables
idades. z0 z
• Manejo de la tabla
A partir de este momento cuando necesites calcular probabilidades con la
normal N (0; 1), pulsa en el icono de la derecha
Tabla N(0,1)
y luego regresas al lugar donde estabas con el icono de la derecha
Volver Tabla N(0,1)
Ahora vas a aprender a a manejar la tabla N (0; 1).
Doc Doc
Volver Cerrar

29. MATEMATICAS
Secci´n 4: La Distribuci´n Normal
o o 29 2º Bachillerato
r=A+lu
Caso I P (Z ≤ z0 ) y z0 es positivo. A
Para calcular P (Z ≤ 1.25) = Φ(1.25), procedemos de la siguiente forma.
d
Buscamos en la tabla de la N (0; 1) el valor 1.25. En la primera columna B
de la tabla se busca el valor 1.2 y en esta fila nos desplazamos hasta la s=B+mv
SOCIALES
columna con cabecera 0.05, obteniendo el valor 0.8944.
Caso II P (Z ≤ −z0 ) y −z0 es negativo. MaTEX
Se utiliza por simetr´ la siguiente propiedad
ıa
Aleatorias
P (Z ≤ −z0 ) = Φ(−z0 ) = 1 − Φ(z0 )
Variables
Para calcular P (Z ≤ −1.34) = 1 − Φ(1.34), procedemos de la misma
forma. Buscamos en la tabla de la N (0; 1) el valor 1.34. En la primera
columna de la tabla se busca el valor 1.3 y en esta fila nos desplazamos
hasta la columna con cabecera 0.04, obteniendo el valor 0.9099. Luego
P (Z ≤ −1.34) = 1 − Φ(1.34) = 1 − 0.9099 = 0, 0901
Caso III P (z0 ≤ Z ≤ z1 )
Se calcula Φ(z1 ) y Φ(z0 ) y se restan, por la f´rmula
o
P (z0 ≤ Z ≤ z1 ) = Φ(z1 ) − Φ(z0 ) Tabla N(0,1)
As´ por ejemplo
ı
P (1.25 ≤ Z ≤ 1.34) = Φ(1.34) − Φ(1.25) = 0.9099 − 0.8944 = 0, 0155
Doc Doc
Volver Cerrar

30. MATEMATICAS
Secci´n 4: La Distribuci´n Normal
o o 30 2º Bachillerato
r=A+lu
Ejemplo 4.1. Si z es normal Nz (0; 1) hallar: A
P (z ≤ 0) P (z ≤ 1) P (z ≤ 2) d
B
Soluci´n:
o s=B+mv
SOCIALES
Utiliza la Tabla N(0,1) MaTEX
Aleatorias
Variables
P (z ≤ 0) = Φ(0) = 0.5
Φ(0)
0 z
P (z ≤ 1) = Φ(1) = 0.8413
Φ(1)
1 z
P (z ≤ 2) = Φ(2) = 0.97725 Tabla N(0,1)
Φ(2)
2 z Doc Doc
Volver Cerrar

31. MATEMATICAS
Secci´n 4: La Distribuci´n Normal
o o 31 2º Bachillerato
r=A+lu
Ejemplo 4.2. Si z es normal Nz (0; 1) hallar: A
P (z ≤ −1) P (z 1) P (z 2) d
B
Soluci´n:
o s=B+mv
SOCIALES
Utiliza la Tabla N(0,1) MaTEX
Aleatorias
Φ(−1)
Variables
P (z ≤ −1) = Φ(−1) = 1−Φ(1) = 0.1587
−1 z
P (z 1) = 1 − Φ(1) = 0.1587
Φ(1)
1 z
P (z 2) = 1 − Φ(2) = 0.02275 Tabla N(0,1)
Φ(2)
2 z Doc Doc
Volver Cerrar

32. MATEMATICAS
Secci´n 4: La Distribuci´n Normal
o o 32 2º Bachillerato
r=A+lu
Ejemplo 4.3. Si z es normal Nz (0; 1) hallar: A
P (−1 z 1) P (0 z 2) P (1 z 2) d
B
Soluci´n:
o s=B+mv
SOCIALES
Utiliza la Tabla N(0,1) MaTEX
Aleatorias
Variables
P (−1 z 1) =Φ(1) − Φ(−1)
=2 Φ(1) − 1
=0, 6826
−1 1 z
P (0 z 2) =Φ(2) − Φ(0) =
=0.97725 − 0.5
=0, 47725
0 2 z
Tabla N(0,1)
P (1 z 2) =Φ(2) − Φ(1)
=0, 13595
1 2 z Doc Doc
Volver Cerrar

33. MATEMATICAS
Secci´n 4: La Distribuci´n Normal
o o 33 2º Bachillerato
Ahora vas a manejar la tabla en forma inversa. Nos dan la probabilidad
r=A+lu
A
y calculamos el valor de la variable z0 que acumula dicha probabilidad.
d
Ejemplo 4.4. Hallar z0 de la normal Nz (0; 1) en cada caso: B
s=B+mv
SOCIALES
P (z z0 ) = 0.7019 P (z z1 ) = 0.8997 P (z z2 ) = 0.9625
Soluci´n:
o MaTEX
Utiliza la Tabla N(0,1)
Aleatorias
Variables
• Φ(z0 ) = 0.7019, se busca en la parte central de la tabla normal Nz (0; 1)
la probabilidad 0.7019, observando su fila 0.5 y su columna 0.03, luego
Φ(z0 ) = 0.7019 =⇒ z0 = 0.53
• Φ(z1 ) = 0.8997, se busca en la parte central de la tabla normal Nz (0; 1)
la probabilidad 0.8997, observando su fila 1.2 y su columna 0.08, luego
Φ(z1 ) = 0.8997 =⇒ z1 = 1.28
• Φ(z2 ) = 0.9625, se busca en la parte central de la tabla normal Nz (0; 1)
la probabilidad 0.9625, observando su fila 1.7 y su columna 0.08, luego
Tabla N(0,1)
Φ(z2 ) = 0.9625 =⇒ z2 = 1.78
Doc Doc
Volver Cerrar

34. MATEMATICAS
Secci´n 4: La Distribuci´n Normal
o o 34 2º Bachillerato
r=A+lu
• Tipificar una variable normal A
Cuando tenemos una variable normal N (µ; σ), para calcular las probabil- d
idades se efect´a un cambio de variable que la convierte en una del tipo
u B
s=B+mv
N (0; 1): SOCIALES
X −µ
X ∼ N (µ; σ) =⇒ Z = ∼ N (0; 1)
σ
A esta variable se la llama normalizada o tipificada. De esta forma, s´lo es
o
MaTEX
Aleatorias
necesario disponer de la tabla correspondiente a la N (0, 1) para realizar un
c´lculo dado, ya que
a
Variables
x0 − µ
PX (X ≤ x0 ) = PZ Z ≤ .
σ
Ejemplo 4.5. Si X es normal N (5; 2) hallar P (X 8).
Soluci´n:
o
Tipificamos
X −5 8−5
P (X 8) =P
2 2 Tabla N(0,1)
=P (z 1.5) = Φ(1.5)
=0.9332 5 8 X
Doc Doc
Volver Cerrar

35. MATEMATICAS
Secci´n 4: La Distribuci´n Normal
o o 35 2º Bachillerato
r=A+lu
Ejemplo 4.6. Si X es normal N (5; 2) hallar: Utiliza la Tabla N(0,1) A
P (X 8) P (X 2) P (2 X 8) d
B
s=B+mv
Soluci´n:
o SOCIALES
P (X 8) =P
X −5
8−5 MaTEX
2 2
Aleatorias
=P (z 1.5) = Φ(1.5)
Variables
=0.9332 5 8 X
X −5 2−5
P (X 2) =P
2 2
=P (z −1.5)
=1 − Φ(1.5) = 0.0668
2 5 X
2−5 8−5
P (2 X 8) =P z
2 2
=P (−1.5 z 1.5)
Tabla N(0,1)
=Φ(1.5) − Φ(−1.5)
=0.8664
2 5 8 X
Doc Doc
Volver Cerrar

36. MATEMATICAS
Secci´n 4: La Distribuci´n Normal
o o 36 2º Bachillerato
r=A+lu
Ejercicio 13. En una distribuci´n normal N (18; 4), hallar las siguientes
o A
probabilidades:
d
a) P (x 18)
B
b) P (x 20) s=B+mv
SOCIALES
c) P (x 16, 5)
d) P (x 11)
e) P (19 x 23)
MaTEX
f ) P (11 x 25)
Aleatorias
Variables
Utiliza la Tabla N(0,1)
Ejercicio 14. En la distribuci´n normal Nz (0; 1), hallar el valor de z0 en
o
cada caso
a) P (z z0 ) = 0.50
b) P (z z0 ) = 0.8729 Tabla N(0,1)
c) P (z z0 ) = 0.3300
d) P (z z0 ) = 0.9015
e) P (z z0 ) = 0.9971
f ) P (z z0 ) = 0.1190 Doc Doc
Volver Cerrar

37. MATEMATICAS
Secci´n 4: La Distribuci´n Normal
o o 37 2º Bachillerato
r=A+lu
Ejemplo 4.7. Si la estatura X de 500 estudiantes es normal de media 172 A
cm y desviaci´n t´
o ıpica 5 cm, hallar el n´mero de estudiantes con estatura
u
d
a) entre 170 y 175 cm b) mayor de 180 cm B
s=B+mv
SOCIALES
Soluci´n:
o
Por comodidad, tipificamos los valores que vamos a usar
170 − 172 175 − 172 180 − 172
MaTEX
z1 = = −0.4 z2 = = 0.6 z3 = = 1.6
Aleatorias
5 5 5
Variables
P (170 X 175) =P (−0.4 z 0.6)
=Φ(0.6) − Φ(−0.4)
=0.3811
N = 500 × 0.3811 ≈ 190 estudiantes −0.4 0.6 z
P (X 180) =P (z 1.6)
=1 − Φ(1.6) Tabla N(0,1)
=0.0548
N = 500 × 0.0548 ≈ 27 estudiantes 1.6 z
Doc Doc
Volver Cerrar

38. MATEMATICAS
Secci´n 4: La Distribuci´n Normal
o o 38 2º Bachillerato
r=A+lu
4.2. Ejercicios A
Ejercicio 15. La temperatura T durante el mes de mayo est´ distribuida de
a d
forma normal con media 21o y desviaci´n t´
o ıpica 4o . Hallar el n´mero de d´
u ıas B
s=B+mv
esperados en que haya una temperatura entre 19o y 23o . SOCIALES
Ejercicio 16. El tiempo en d´ de duraci´n de los focos producidos por una
ıas o
empresa, es una variable normal de media 780 y desviaci´n t´
o ıpica de 40 d´ıas.
MaTEX
Aleatorias
Calc´lese el porcentaje de focos con una duraci´n superior a 800 d´
u o ıas.
Variables
Ejercicio 17. Los pesos de los individuos de una poblaci´n se distribuyen
o
normalmente con media 70 kg y desviaci´n t´
o ıpica 5 kg. Calcular:
a) La probabilidad de que el peso de un individuo est´ comprendido entre
e
65 y 80 kg.
b) La probabilidad de que un individuo pese m´s de 100 kg.
a
Ejercicio 18. En una panader´ se cortan panecillos con un peso que se
ıa
ajusta a una variable normal de media 100 g y desviaci´n t´
o ıpica 9 g. ¿Cu´l a
es la probabilidad de obtener un panecillo cuyo peso oscile entre 80 g y la
media? Tabla N(0,1)
Ejercicio 19. La distribuci´n de la duraci´n de un embarazo en mujeres
o o
es aproximadamente normal con media 266 d´ y desviaci´n t´
ıas o ıpica 16 d´
ıas.
Calcular:
Doc Doc
a) La probabilidad de que un embarazo dure m´s de 242 d´
a ıas.
Volver Cerrar

39. MATEMATICAS
Secci´n 4: La Distribuci´n Normal
o o 39 2º Bachillerato
r=A+lu
b) El 20% de los embarazos duran menos de ¿cu´ntos d´
a ıas? A
c) El 50% de los embarazos duran menos de ¿cu´ntos d´
a ıas? d
B
Ejercicio 20. Una empresa instala en una ciudad 20.000 bombillas. La du- s=B+mv
SOCIALES
raci´n de una bombilla sigue una distribuci´n normal con media 302 d´ y
o o ıas
desviaci´n t´
o ıpica 40 d´
a
ıas. Calcular:
a) ¿Cu´ntas bombillas se espera que se fundan antes de 365 d´
ıas?
MaTEX
Aleatorias
b) ¿Cu´ntas bombillas durar´n m´s de 400 d´
a a a ıas?
Variables
Ejercicio 21. Una compa˜´ de autobuses conoce que el retraso en la llegada
nıa
sigue una ley normal con media 5 minutos, y que el 68.26% de los autobuses
llega con un retraso comprendido entre los 2 y los 8 minutos:
a) ¿Cu´l es la desviaci´n t´
a o ıpica?.
b) ¿Cu´l es la probabilidad de que un autob´s llegue antes de la hora?.
a u
c) ¿Cu´l es la probabilidad de que un autob´s se retrase de m´s de 10
a u a
minutos?.
Ejercicio 22. Cierto tipo de bater´ dura un promedio de 3 a˜os, con una
ıa n
Tabla N(0,1)
desviaci´n t´
o ıpica de 0,5 a˜os. Suponiendo que la duraci´n de las bater´ es
n o ıas
una variable normal:
a) ¿Qu´ porcentaje de bater´ se espera que duren entre 2 y 4 a˜os?.
e ıas n
b) Si una bater´ lleva funcionando 3 a˜os, ¿ cu´l es la probabilidad de
ıa n a Doc Doc
que dure menos de 4,5 a˜os?
n
Volver Cerrar

40. MATEMATICAS
Secci´n 4: La Distribuci´n Normal
o o 40 2º Bachillerato
r=A+lu
Ejercicio 23. En un examen de matem´ticas, en el que se ha evaluado de
a A
0 a 20 puntos, el 67% de los alumnos ha obtenido una puntuaci´n igual o
o
d
menor que 12,2 y el 9% ha obtenido puntuaci´n superior a 16,7. Suponiendo
o B
que la distribuci´n de las puntuaciones sea normal, calcular su media y su
o s=B+mv
SOCIALES
desviaci´n t´
o ıpica.
Ejercicio 24. Un estudio de un fabricante de televisores indica que la du- MaTEX
raci´n media de un televisor es de 10 a˜os, con una desviaci´n t´
o n o ıpica de
Aleatorias
0,7 a˜os. Suponiendo que la duraci´n media de los televisores sigue una
n o
Variables
distribuci´n normal,
o
a) Calcula la probabilidad de que un televisor dure m´s de 9 a˜os.
a n
b) Calcula la probabilidad de que dure entre 9 y 11
Tabla N(0,1)
Doc Doc
Volver Cerrar

41. MATEMATICAS
Secci´n 5: Aproximaci´n de la distribuci´n binomial por la normal
o o o 41 2º Bachillerato
r=A+lu
5. Aproximaci´n de la distribuci´n binomial por la normal
o o A
Supongamos que X en una variable aleatoria con distribuci´n de probabil-
o d
idad binomial B(n, p) y que el par´metro n tiende a infinito mientras que
a B
s=B+mv
el par´metro p permanece constante. Entonces, puede demostrarse que la
a SOCIALES
funci´n de distribuci´n 1 de la variable aleatoria
o o
Z=
X − np
(11)
MaTEX
np(1 − p)
Aleatorias
Variables
tiende a la funci´n de distribuci´n normal est´ndar. Esto justifica que, si
o o a
np 5 y np(1 − p) 5, se use la aproximaci´n
o
x − np
FX (x) Φ , para x = 0, 1, . . . , n. (12)
np(1 − p)
La aproximaci´n (12) puede mejorarse con la llamada correcci´n por con-
o o
tinuidad, de forma que
x − np + 0.5
FX (x) Φ , para x = 0, 1, . . . , n. (13)
np(1 − p)
Tabla N(0,1)
1 Doc Doc
Debe notarse que la funci´n de probabilidad binomial no tiende a la funci´n de den-
o o
sidad normal est´ndar.
a
Volver Cerrar

42. MATEMATICAS
Secci´n 5: Aproximaci´n de la distribuci´n binomial por la normal
o o o 42 2º Bachillerato
r=A+lu
A
El gr´fico muestra como se
a 0.35
aproxima la binomial a la 0.3
n=12 d
normal, a medida que n au- n=18
B
s=B+mv
0.25
menta n=24
SOCIALES
0.2
0.15
n=30 MaTEX
n=60
Aleatorias
0.1
Variables
0.05
0
0 2 4 6 8 10 12 14 16 18 20
1
Ejemplo 5.1. Sea X binomial B 100; que tiene de media µ = np = 50
2
√ 1 1
yσ= npq = 100 · · = 5. Si aproximamos por una normal N (50; 5),
2 2
se tiene
• Con la Binomial el valor exacto es P (X ≤ 55) = 0.8644
Tabla N(0,1)
• Con la aproximaci´n por la normal el valor es
o
55.5 − 50
P (X ≤ 55) =P z≤ = Φ (1.1) = 0.8643
5
Doc Doc
Volver Cerrar

43. MATEMATICAS
Secci´n 5: Aproximaci´n de la distribuci´n binomial por la normal
o o o 43 2º Bachillerato
r=A+lu
Ejemplo 5.2. Aproximando con una distribuci´n normal, calcular la proba-
o A
bilidad de que al lanzar una moneda 100 veces, el n´mero de caras obtenido
u
d
est´ comprendido entre 46 y 55.
e B
s=B+mv
SOCIALES
45.5 − 50 55.5 − 50
P (46 ≤ X ≤ 55) =P z
5 5 MaTEX
=Φ (1.1) − Φ (−1.1) = 0.7287
Aleatorias
Variables
Utiliza la Tabla
Ejemplo 5.3. El 90% de los miembros de un club pasan sus vacaciones en
la playa. Calcular aproximando con una distribuci´n normal, la probabilidad
o
de que en un grupo de 60 miembros del club, 50 o menos vayan a la playa en
sus vacaciones .
√ √ Tabla N(0,1)
X ∼ B(60; 0.9) ⇒ µ = n p = 60·0.9 = 54 σ= npq = 60 · 0.9 · 0.1 = 2, 32
50.5 − 54
P (X ≤ 50) =P z = Φ (−1, 51) = 1 − Φ(1.51) = 0.0655
2.32 Doc Doc
Volver Cerrar

44. MATEMATICAS
Secci´n 5: Aproximaci´n de la distribuci´n binomial por la normal
o o o 44 2º Bachillerato
r=A+lu
5.1. Ejercicios A
Ejercicio 25. Se lanza una moneda 200 veces. Hallar la probabilidad de d
a) Obtener a lo m´s 95 caras
a B
s=B+mv
SOCIALES
b) Obtener m´s de 110 caras
a
Ejercicio 26. En cierto pa´ la probabilidad de que nazca una ni˜a es 0.58.
ıs n MaTEX
Si se producen en un a˜o 1000 nacimientos, ¿cu´l es la probabilidad de que
n a
Aleatorias
el n´mero de ni˜as nacidas est´ comprendido entre 501 y 550?
u n e
Variables
Ejercicio 27. El 4 % de las reservas de un vuelo no son utilizadas. Seg´n esta
u
observaci´n, una compa˜ia de aviaci´n vende 150 billetes para 140 plazas. ¿
o n o
Cu´l es la probabilidad de que todos los pasajeros consigan plaza?
a
Ejercicio 28. Un concesionario de autom´viles vende a particulares veh´
o ıculos
de la misma marca. Sabiendo que la probabilidad de que este tipo de veh´ ıculos
est´ en servicio dos a˜os despu´s es de 0.8, determinar la probabilidad de que
e n e
de 4000 autom´viles vendidos, m´s de 3120 est´n en servicio dentro de dos
o a e
a˜os.
n
Ejercicio 29. Se lanza un dado 600 veces. Hallar la probabilidad de Tabla N(0,1)
a) Obtener a lo m´s 95 –seises–
a
b) Obtener m´s de 110 –seises–
a
Doc Doc
Volver Cerrar

45. MATEMATICAS
Secci´n 5: Aproximaci´n de la distribuci´n binomial por la normal
o o o 45 2º Bachillerato
r=A+lu
Test. Responde a las cuestiones: A
1. Sea X ≡ B(100; 0.5) entonces su media es: d
(a) µ = 100 (b) µ = 50 (c) otro B
s=B+mv
2. Sea X ≡ B(100; 0.5) entonces su varianza es: SOCIALES
2 2
(a) σ = 100 (b) σ = 25 (c) otro
3. Sea X es una variable aleatoria discreta el significado de FX (a) es :
MaTEX
Aleatorias
(a) P (X a) (b) P (X a) (c) P (X ≤ a)
Variables
4. Sea X es una variable aleatoria continua el significado de FX (a) es :
(a) P (X a) (b) P (X ≤ a) (c) las dos
5. Sea X es una variable aleatoria discreta se tiene:
(a) P (X a) = 1 − FX (x) (b) P (X ≥ a) = 1 − FX (x)
6. Si X ≡ B(4; 0.2) se puede aproximar a una normal:
(a) Si (b) No
7. Si X ≡ B(40; 0.2) se puede aproximar a una normal:
(a) Si (b) No
Tabla N(0,1)
Doc Doc
Volver Cerrar

46. MATEMATICAS
2º Bachillerato
r=A+lu
z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09
A
Tabla Normal N(0; 1)
0.0 .5000 .5040 .5080 .5120 .5160 .5199 .5239 .5279 .5319 .5359
0.1 .5398 .5438 .5478 .5517 .5557 .5596 .5636 .5675 .5714 .5753 d
0.2 .5793 .5832 .5871 .5910 .5948 .5987 .6026 .6064 .6103 .6141
0.3 .6179 .6217 .6255 .6293 .6331 .6368 .6406 .6443 .6480 .6517 B
s=B+mv
0.4 .6554 .6591 .6628 .6664 .6700 .6736 .6772 .6808 .6844 .6879 SOCIALES
0.5 .6915 .6950 .6985 .7019 .7054 .7088 .7123 .7157 .7190 .7224
0.6
0.7
0.8
.7257
.7580
.7881
.7291
.7611
.7910
.7324
.7642
.7939
.7357
.7673
.7967
.7389
.7704
.7995
.7422
.7734
.8023
.7454
.7764
.8051
.7486
.7794
.8078
.7517
.7823
.8106
.7549
.7852
.8133
MaTEX
Aleatorias
0.9 .8159 .8186 .8212 .8238 .8264 .8289 .8315 .8340 .8365 .8389
1.0 .8413 .8438 .8461 .8485 .8508 .8531 .8554 .8577 .8599 .8621
Variables
1.1 .8643 .8665 .8686 .8708 .8729 .8749 .8770 .8790 .8810 .8830
1.2 .8849 .8869 .8888 .8907 .8925 .8944 .8962 .8980 .8997 .9015
1.3 .9032 .9049 .9066 .9082 .9099 .9115 .9131 .9147 .9162 .9177
1.4 .9192 .9207 .9222 .9236 .9251 .9265 .9279 .9292 .9306 .9319
1.5 .9332 .9345 .9357 .9370 .9382 .9394 .9406 .9418 .9429 .9441
1.6 .9452 .9463 .9474 .9484 .9495 .9505 .9515 .9525 .9535 .9545
1.7 .9554 .9564 .9573 .9582 .9591 .9599 .9608 .9616 .9625 .9633
1.8 .9641 .9649 .9656 .9664 .9671 .9678 .9686 .9693 .9699 .9706
1.9 .9713 .9719 .9726 .9732 .9738 .9744 .9750 .9756 .9761 .9767
2.0 .9772 .9778 .9783 .9788 .9793 .9798 .9803 .9808 .9812 .9817
2.1 .9821 .9826 .9830 .9834 .9838 .9842 .9846 .9850 .9854 .9857
2.2 .9861 .9864 .9868 .9871 .9875 .9878 .9881 .9884 .9887 .9890
2.3 .9893 .9896 .9898 .9901 .9904 .9906 .9909 .9911 .9913 .9916
2.4 .9918 .9920 .9922 .9925 .9927 .9929 .9931 .9932 .9934 .9936
2,5 .9938 .9940 .9941 .9943 .9945 .9946 .9948 .9949 .9951 .9952 Tabla N(0,1)
2.6 .9953 .9955 .9956 .9957 .9959 .9960 .9961 .9962 .9963 .9964
2.7 .9965 .9966 .9967 .9968 .9969 .9970 .9971 .9972 .9973 .9974
2.8 .9974 .9975 .9976 .9977 .9977 .9978 .9979 .9979 .9980 .9981
2.9 .9981 .9982 .9982 .9983 .9984 .9984 .9985 .9985 .9986 .9986
3.0 .9987 .9987 .9987 .9988 .9988 .9989 .9989 .9989 .9990 .9990
Doc Doc
Φ(−z) = 1 − Φ(z)
Volver Cerrar

47. MATEMATICAS
Soluciones a los Ejercicios 47 2º Bachillerato
r=A+lu
Soluciones a los Ejercicios A
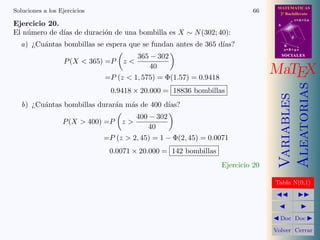
Ejercicio 1. Planteamos tres ecuaciones con tres inc´gnitas
o d
4 B
s=B+mv
p(xi ) = 1 ⇒0.1 + a + b + c + 0.2 = 1 SOCIALES
i=0
P (X ≤ 2) = 0.75 ⇒px (0) + px (1) + px (2) = 0.75 MaTEX
P (X ≥ 2) = 0.75 ⇒px (2) + px (3) + px (4) = 0.75
Aleatorias
Variables
luego 
a + b + c = 0.7 
a + b = 0.65 a = 0.15 b = 0.5 c = 0.05
b + c = 0.55

La esperanza de x, E[x] = µ es
µ =0 · 0.1 + 1 · 0.15 + 2 · 0.5 + 3 · 0.05 + 4 · 0.2 = 2.8
La varianza de x, σ 2 es
σ 2 =02 · 0.1 + 12 · 0.15 + 22 · 0.5 + 32 · 0.05 + 42 · 0.2 − 2.82
Tabla N(0,1)
=2.04
√
σ = 2.04 = 1.43
Ejercicio 1
Doc Doc
Volver Cerrar

48. MATEMATICAS
Soluciones a los Ejercicios 48 2º Bachillerato
r=A+lu
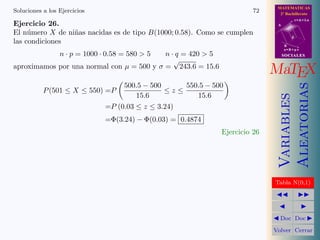
Ejercicio 2. Hallamos la funci´n de probabilidad para la ganancia X del
o A
juego, teniendo en cuenta que
d
8 B
P (X = 15) = P ( una sota o un caballo ) = s=B+mv
40 SOCIALES
8
P (X = 5) = P ( un rey o un as ) =
40 MaTEX
24
P (X = −4) = P ( otra carta ) =
Aleatorias
40
Variables
xi 15 5 −4
8 8 24
px (xi )
40 40 40
La ganancia esperanza de x, E[x] = µ es
8 8 24 64
µ =15 · +5· −4· = = 1.6 cts
40 40 40 40
Ejercicio 2
Tabla N(0,1)
Doc Doc
Volver Cerrar

49. MATEMATICAS
Soluciones a los Ejercicios 49 2º Bachillerato
r=A+lu
Ejercicio 3. A
Sea N bola negra, del diagrama se tiene 2 d
a) Probabilidad de sacar bola negra: 6 B
2N s=B+mv
SOCIALES
1 2 1 1 1 1 1 4R
P (N ) = · + · + · = 1 4
3 6 3 2 3 6 3 3 UA 6 MaTEX
y la probabilidad de sacar bola roja: 1
Aleatorias
2
2 3N
Variables
P (R) = 1 − P (N ) =
3 1 3R
1
3
b) La ganancia esperada es: UB 2
1 1
E[G] = 3 · P (R) + 0 · P (N ) 3 6
2 1 1N
= 3 · + 0 · = 2 euros 5R
3 3 5
UC 6
Ejercicio 3
Tabla N(0,1)
Doc Doc
Volver Cerrar

50. MATEMATICAS
Soluciones a los Ejercicios 50 2º Bachillerato
r=A+lu
Ejercicio 4. A
4 4 6 6·5 d
a) = =4 b) = = 15
1 1 2 2·1 B
s=B+mv
8 8·7·6 10 10 · 9 SOCIALES
c) = = 56 d) = = 45
3 3·2·1 2 2·1
5 7 7·6·5 MaTEX
e) =1 f) = = 35
0 3 3·2·1
Aleatorias
9 9·8·7·6 13 13 · 12
Variables
g) = = 126 h) = = 78
4 4·3·2·1 2 2·1
Ejercicio 4
Tabla N(0,1)
Doc Doc
Volver Cerrar

51. MATEMATICAS
Soluciones a los Ejercicios 51 2º Bachillerato
r=A+lu
Ejercicio 5. A
Sea X el n´mero de encestes en cinco lanzamientos
u
d
X es B(n = 5; p = 0.3) B
s=B+mv
SOCIALES
La probabilidad de que enceste, exactamente dos canastas de cinco
lanzamientos
5 2 3
MaTEX
P (X = 2) = (0.3) (0.7) = 0.3087
Aleatorias
2
Variables
Ejercicio 5
Tabla N(0,1)
Doc Doc
Volver Cerrar

52. MATEMATICAS
Soluciones a los Ejercicios 52 2º Bachillerato
r=A+lu
Ejercicio 6. A
Se tiene que el n´mero X de alumnos que se licencian en 5 a˜os
u n
d
X es B(n = 10; p = 0.4) B
s=B+mv
SOCIALES
a) la probabilidad de que ninguno se licencie en 5 a˜os.
n
P (X = 0) =
10 0
(0.4) (0.6)
10
= 0.0060 MaTEX
0
Aleatorias
b) la probabilidad de que todos se licencien en 5 a˜os.
n
Variables
10 10 0
P (X = 10) = (0.4) (0.6) = 0.0001
10
c) la probabilidad de que un unico estudiante se licencie en 5 a˜os.
´ n
10 1 9
P (X = 1) = (0.4) (0.6) = 0.0403
1
Ejercicio 6
Tabla N(0,1)
Doc Doc
Volver Cerrar

53. MATEMATICAS
Soluciones a los Ejercicios 53 2º Bachillerato
r=A+lu
Ejercicio 7. A
Se tiene que el n´mero de piezas defectuosas X
u
d
X es B(n = 40; p = 0.012) B
s=B+mv
SOCIALES
a) la probabilidad de que s´lo haya una defectuosa.
o
P (X = 1) =
40 1
(0.012) (0.988)
39
= 0.6170 MaTEX
1
Aleatorias
b) la probabilidad de que no haya ninguna defectuosa.
Variables
40 0 40
P (X = 0) = (0.012) (0.988) = 0.299
0
Ejercicio 7
Tabla N(0,1)
Doc Doc
Volver Cerrar

54. MATEMATICAS
Soluciones a los Ejercicios 54 2º Bachillerato
r=A+lu
Ejercicio 8. A
Se tiene que el n´mero de alumnos que faltan X
u
d
X es B(n = 20; p = 0.04) B
s=B+mv
SOCIALES
a) la probabilidad de que no se registre ninguna falta.
P (X = 0) =
20 0
(0.04) (0.96)
20
= 0.4420 MaTEX
0
Aleatorias
b) la probabilidad de que falten a clase menos de tres estudiantes.
Variables
20 0 20 20 1 19
P (X 3) = (0.04) (0.96) + (0.04) (0.96) +
0 1
20 2 18
+ (0.04) (0.96) = 0.9561
2
c) la probabilidad de que falte a clase un unico estudiante.
´
20 1 19
P (X = 1) = (0.04) (0.96) = 0.3683
1
Ejercicio 8 Tabla N(0,1)
Doc Doc
Volver Cerrar

55. MATEMATICAS
Soluciones a los Ejercicios 55 2º Bachillerato
r=A+lu
Ejercicio 9. A
En una familia de 5 hijos, se tiene que el n´mero de ni˜as X
u n
d
X es B(n = 5; p = 0.56) B
s=B+mv
SOCIALES
a) la probabilidad de que tenga exactamente tres ni˜as.
n
P (X = 3) =
5 3 2
(0.56) (0.44) = 0.3400 MaTEX
3
Aleatorias
b) la probabilidad de que tenga al menos dos ni˜as.
n
Variables
5 2 3 5 3 2
P (X ≥ 2) = (0.56) (0.44) + (0.56) (0.44) +
2 3
5 4 1 5 5 0
(0.56) (0.44) + (0.56) (0.44) = 0.8235
4 5
c) el n´mero medio de hijas en las familias con cinco hijos es la media de
u
esta binomial
µ = np = 5 · 0.56 = 2, 8
Ejercicio 9 Tabla N(0,1)
Doc Doc
Volver Cerrar

56. MATEMATICAS
Soluciones a los Ejercicios 56 2º Bachillerato
r=A+lu
Ejercicio 10. A
Se tiene que el n´mero de asistentes X
u
d
X es B(n = 8; p = 0.85) B
s=B+mv
SOCIALES
a) la probabilidad de asistan todas.
P (X = 8) =
8 8 0
(0.85) (0.15) = 0.3847 MaTEX
8
Aleatorias
b) la probabilidad de asistan m´s de 6 personas.
a
Variables
8 7 1 8 8 0
P (X ≥ 7) = (0.85) (0.15) + (0.85) (0.15) = 0.6223
7 8
c) la probabilidad de asista al menos la mitad.
8 4 8 4 5 3
P (X ≥ 4) = (0.85) (0.15) + (0.85) (0.15) +
4 5
8 6 2 8 7 1
(0.85) (0.15) + (0.85) (0.15) +
6 7
8 8 0 Tabla N(0,1)
(0.85) (0.15) = 0.7273
8
Ejercicio 10
Doc Doc
Volver Cerrar

57. MATEMATICAS
Soluciones a los Ejercicios 57 2º Bachillerato
r=A+lu
Ejercicio 11. A
Se tiene que el n´mero de piezas defectuosas X
u
d
X es B(n = 4; p = 0.2) B
s=B+mv
SOCIALES
luego, la probabilidad de que entre cuatro piezas elegidas al azar, a lo sumo
2 sean defectuosas es
4 0 4 4 1 3
MaTEX
P (X ≤ 2) = (0.2) (0.8) + (0.2) (0.8) +
Aleatorias
0 1
Variables
4 2 2
(0.2) (0.8) = 0.9728
2
Ejercicio 11
Tabla N(0,1)
Doc Doc
Volver Cerrar

58. MATEMATICAS
Soluciones a los Ejercicios 58 2º Bachillerato
r=A+lu
Ejercicio 12. A
Sea X el n´mero de veces que se cae el patinador, se tiene que
u
d
X es B(n = 5; p = 0.4) B
s=B+mv
SOCIALES
luego, la probabilidad de que de que se caiga al menos 3 veces.
p(X ≥ 3) =
5 3 2
(0.4) (0.6) +
5 4 1
(0.4) (0.6) + MaTEX
3 4
Aleatorias
5 5 0
(0.4) (0.6) = 0.3174
Variables
5
Ejercicio 12
Tabla N(0,1)
Doc Doc
Volver Cerrar

59. MATEMATICAS
Soluciones a los Ejercicios 59 2º Bachillerato
r=A+lu
Ejercicio 13. A
X − 18
Se tipifica con z = d
4
B
a) P (x 18) = Φ(0) = 0.50 s=B+mv
SOCIALES
b) P (x 28) = Φ(2.5) = 0.9938
c) P (x 16.4) = 1 − Φ(−0.4) = Φ(0.4) = .6554 MaTEX
d ) P (x 11) = Φ(−1.75) = 1 − Φ(1.75) = 1 − 0.9599 = 0.0401
Aleatorias
e) P (19 x 23) = Φ(1.25) − Φ(0.25) = 0.8944 − 0.5987 = 0.2957
Variables
f ) P (11 x 25) = Φ(1.75) − Φ(−1.75) = 2 Φ(1.75) − 1 = 0, 9198
Ejercicio 13
Tabla N(0,1)
Doc Doc
Volver Cerrar

60. MATEMATICAS
Soluciones a los Ejercicios 60 2º Bachillerato
r=A+lu
Ejercicio 14. A
a) P (z z0 ) = Φ(z0 ) = 0.50 ⇒ z0 = 0 d
b) P (z z0 ) = Φ(z0 ) = 0.8729 ⇒ z0 = 1.14 B
s=B+mv
SOCIALES
c) P (z z0 ) = Φ(z0 ) = 0.3300 ⇒ Φ(−z0 ) = 0.6700 ⇒ z0 = −0.44
d ) P (z z0 ) = 1 − Φ(z0 ) = 0.9015 = Φ(1.29) ⇒ z0 = −1.29 MaTEX
e) P (z z0 ) = Φ(z0 ) = 0.9971 ⇒ z0 = 2.76
Aleatorias
f ) P (z z0 ) = 1 − Φ(z0 ) = 0.1190 ⇒ Φ(z0 ) = 0.8810 ⇒ z0 = 1.18
Variables
Ejercicio 14
Tabla N(0,1)
Doc Doc
Volver Cerrar

61. MATEMATICAS
Soluciones a los Ejercicios 61 2º Bachillerato
r=A+lu
Ejercicio 15. A
La temperatura T ∼ N (21; 4):
d
B
19 − 21 23 − 21 s=B+mv
P (19 T 23) =P z SOCIALES
4 4
=P (−0.5 z 0.5) = Φ(0.5) − Φ(0.5) = 0, 383 MaTEX
Aleatorias
0.383 × 30 ≈ 11 d´
ıas
Variables
Ejercicio 15
Tabla N(0,1)
Doc Doc
Volver Cerrar

62. MATEMATICAS
Soluciones a los Ejercicios 62 2º Bachillerato
r=A+lu
Ejercicio 16. A
El tiempo X ∼ N (780; 40):
d
B
800 − 780 s=B+mv
P (X 800) =P X SOCIALES
40
=P (z 0.5) = 1 − Φ(0.5) = 0, 3085 MaTEX
Aleatorias
Ejercicio 16
Variables
Tabla N(0,1)
Doc Doc
Volver Cerrar

63. MATEMATICAS
Soluciones a los Ejercicios 63 2º Bachillerato
r=A+lu
Ejercicio 17. A
El peso X de un individuo es X ∼ N (70; 5):
d
a) La probabilidad de que el peso de un individuo est´ comprendido
e B
s=B+mv
entre 65 y 80 kg. SOCIALES
65 − 70 80 − 70
P (65 X 80) =P
5
z
5 MaTEX
=P (−1 z 2) = Φ(2) − Φ(−1)
Aleatorias
Variables
=Φ(2) + Φ(1) − 1 = 0.8185
b) La probabilidad de que un individuo pese m´s de 100 kg.
a
100 − 70
P (X 100) =P z
5
=P (z 6) = 1 − Φ(6) ≈ 0
Ejercicio 17
Tabla N(0,1)
Doc Doc
Volver Cerrar

64. MATEMATICAS
Soluciones a los Ejercicios 64 2º Bachillerato
r=A+lu
Ejercicio 18. A
El peso X es X ∼ N (100; 9):
d
B
80 − 100 100 − 100 s=B+mv
P (80 X 100) =P z SOCIALES
9 9
=P (−2.22 z 0) = Φ(0) − Φ(−2.22) MaTEX
=Φ(0) + Φ(2.22) − 1 = 0.4868
Aleatorias
Variables
Ejercicio 18
Tabla N(0,1)
Doc Doc
Volver Cerrar

65. MATEMATICAS
Soluciones a los Ejercicios 65 2º Bachillerato
r=A+lu
Ejercicio 19. A
El n´mero de d´ de duraci´n X ∼ N (266; 16):
u ıas o
d
a) La probabilidad de que un embarazo dure m´s de 242 d´
a ıas. B
s=B+mv
242 − 266 SOCIALES
P (X 242) =P z
16
=P (z −1.5) = Φ(1.5) = 0.3811
MaTEX
Aleatorias
b) El 20% de los embarazos duran menos de ¿cu´ntos d´
a ıas?
Variables
P (X x0 ) =0.2 = Φ(−0.84)
x0 − 266
⇒ − 0.84 = ⇒ x0 = 252, 56 d´
ıas
16
c) El 50% de los embarazos duran menos de ¿cu´ntos d´
a ıas?
P (X x0 ) =0.5 = Φ(0)
x0 − 266
⇒0 = ⇒ x0 = 266 d´
ıas
16
Ejercicio 19 Tabla N(0,1)
Doc Doc
Volver Cerrar

66. MATEMATICAS
Soluciones a los Ejercicios 66 2º Bachillerato
r=A+lu
Ejercicio 20. A
El n´mero de d´ de duraci´n de una bombilla es X ∼ N (302; 40):
u ıas o
d
a) ¿Cu´ntas bombillas se espera que se fundan antes de 365 d´
a ıas? B
s=B+mv
365 − 302 SOCIALES
P (X 365) =P z
40
=P (z 1, 575) = Φ(1.57) = 0.9418
MaTEX
Aleatorias
0.9418 × 20.000 = 18836 bombillas
Variables
b) ¿Cu´ntas bombillas durar´n m´s de 400 d´
a a a ıas?
400 − 302
P (X 400) =P z
40
=P (z 2, 45) = 1 − Φ(2, 45) = 0.0071
0.0071 × 20.000 = 142 bombillas
Ejercicio 20
Tabla N(0,1)
Doc Doc
Volver Cerrar

67. MATEMATICAS
Soluciones a los Ejercicios 67 2º Bachillerato
r=A+lu
Ejercicio 21. A
Se sabe que el tiempo de retraso X en minutos es X ∼ N (5; σ) y que
d
P (2 X 8) = 0.6826: B
s=B+mv
a) ¿Cu´l es la desviaci´n t´
a o ıpica?. SOCIALES
2−5 8−5 3 3
P (2 X 8) =P
σ
z
σ
=P − z
σ σ MaTEX
Aleatorias
3 3 3
=Φ −Φ − = 2Φ − 1 = 0.6826
Variables
σ σ σ
3 3
⇒Φ( ) = 0.8413 = Φ(1) ⇒ = 1 ⇒ σ = 3
σ σ
b) probabilidad de que llegue puntual o antes de la hora
0−5
P (X 0) =P z = Φ(−1.67) = 1 − Φ(1.67) = 0, 0475
3
c) prob. de que llegue con un retraso de m´s de 10 minutos?
a
10 − 5
P (X 10) =P z = 1 − Φ(1.67) = 0, 0475 Tabla N(0,1)
3
Ejercicio 21
Doc Doc
Volver Cerrar

68. MATEMATICAS
Soluciones a los Ejercicios 68 2º Bachillerato
r=A+lu
Ejercicio 22. A
Se sabe que el tiempo de duraci´n X en a˜os es X ∼ N (3; 0.5)
o n
d
a) ¿Qu´ porcentaje de bater´ se espera que duren entre 2 y 4 a˜os?.
e ıas n B
s=B+mv
2−3 4−3 SOCIALES
P (2 X 4) =P z
0.5 0.5
=Φ (2) − Φ (−2) = 2 Φ (2) − 1 = 0, 9544
MaTEX
Aleatorias
b) Si una bater´ lleva funcionando 3 a˜os, ¿ cu´l es la probabilidad de
ıa n a
Variables
que dure menos de 4,5 a˜os?
n
P (3 X 4.5)
P (X 4.5|X 3) =
P (X 3)
Φ(3) − Φ(0) 0.4987
= = = 0.9974
1 − Φ(0) 0.5
Ejercicio 22
Tabla N(0,1)
Doc Doc
Volver Cerrar

69. MATEMATICAS
Soluciones a los Ejercicios 69 2º Bachillerato
r=A+lu
Ejercicio 23. A
Se sabe que la puntuaci´n X de un alumno es X ∼ N (µ; σ) con µ y σ
o
d
desconocidas. B
s=B+mv
SOCIALES
12.2 − µ
P (X ≤ 12.2) =P z = 0.6700 = Φ(0.44)
σ MaTEX
12.2 − µ
⇒ = 0.44 (1)
Aleatorias
σ
Variables
16.7 − µ
P (X 16.7) =1 − P z = 0.09 = 1 − Φ(1.34)
σ
16.7 − µ
⇒ = 1.34 (2)
σ
Resolviendo el sistema con (1) y (2)
12.2 − µ = 0.44 σ
4.5 = 0.9 σ =⇒ σ = 5 µ = 10
16.7 − µ = 1.34 σ
Ejercicio 23
Tabla N(0,1)
Doc Doc
Volver Cerrar

70. MATEMATICAS
Soluciones a los Ejercicios 70 2º Bachillerato
r=A+lu
Ejercicio 24. A
Se sabe que la duraci´n media de los televisores sigue una distribuci´n
o o
d
normal, B
X ∼ N (µ = 10; σ = 0.7) s=B+mv
SOCIALES
a) Calcula la probabilidad de que un televisor dure m´s de 9 a˜os.
a n
P (X 9) =1 − P z
9 − 10 MaTEX
0.7
Aleatorias
=1 − Φ(−1.43) = Φ(1.43) = 0.9236
Variables
b) Calcula la probabilidad de que dure entre 9 y 11
9 − 10 11 − 10
P (9 X 11) =P z
0.7 0.7
=Φ (1.43) − Φ (−1.43)
=2 Φ (1.43) − 1 = 0, 8473
Ejercicio 24
Tabla N(0,1)
Doc Doc
Volver Cerrar

71. MATEMATICAS
Soluciones a los Ejercicios 71 2º Bachillerato
r=A+lu
Ejercicio 25. A
1
El n´mero X de caras es de tipo B(200; ). Como se cumplen las
u d
2
condiciones n · p = √ 5 y n · q = 100 5, aproximamos por una normal
100 B
s=B+mv
con µ = 100 y σ = 25 = 5 SOCIALES
a) Obtener a lo m´s 95 caras
a
95.5 − 100
MaTEX
P (X ≤ 95) =P z≤
Aleatorias
5
Variables
=P (z ≤ −0.9) = Φ(−0.9) = 1 − Φ(0.9) = 0, 1841
b) Obtener m´s de 110 caras
a
P (X 110) =1 − P (X ≤ 110)
110.5 − 100
=1 − P z≤
5
=1 − P (z ≤ 2.1) = 1 − Φ(2.1) = 0.0179
Ejercicio 25
Tabla N(0,1)
Doc Doc
Volver Cerrar

72. MATEMATICAS
Soluciones a los Ejercicios 72 2º Bachillerato
r=A+lu
Ejercicio 26. A
El n´mero X de ni˜as nacidas es de tipo B(1000; 0.58). Como se cumplen
u n
d
las condiciones B
s=B+mv
n · p = 1000 · 0.58 = 580 5
n · q = 420 5 SOCIALES
√
aproximamos por una normal con µ = 500 y σ = 243.6 = 15.6
MaTEX
500.5 − 500 550.5 − 500
Aleatorias
P (501 ≤ X ≤ 550) =P ≤z≤
15.6 15.6
Variables
=P (0.03 ≤ z ≤ 3.24)
=Φ(3.24) − Φ(0.03) = 0.4874
Ejercicio 26
Tabla N(0,1)
Doc Doc
Volver Cerrar

73. MATEMATICAS
Soluciones a los Ejercicios 73 2º Bachillerato
r=A+lu
Ejercicio 27. Sea X el n´mero de reservas anuladas de entre los 150
u A
billetes, entonces, como X ∼ B(150; 0.04). Para que todos los pasajeros
d
consigan plaza se necesitan al menos 10 anulaciones, luego por la B
distribuci´n binomial
o s=B+mv
SOCIALES
i=9
150 i 150−i
P (X ≥ 10) = 1 − P (X ≤ 9) = 1 −
i=0
i
p q MaTEX
Aleatorias
Este c´lculo se puede evitar aproximando a la normal. Como se cumplen las
a
Variables
condiciones
n · p = 150 · 0.04 = 6 5 n · q = 144 5
aproximamos por una normal con
√ √
µ=n·p=6 σ = n · p · q = 5.76 = 2.4
P (X ≥ 10) =1 − P (X ≤ 9)
9.5 − 6
=1 − P z≤
2.4
=1 − P (z ≤ 1.46) = 1 − Φ(1.46) = 0.0721
Tabla N(0,1)
Ejercicio 27
Doc Doc
Volver Cerrar

74. MATEMATICAS
Soluciones a los Ejercicios 74 2º Bachillerato
r=A+lu
Ejercicio 28. El n´mero de veh´
u ıculos X de los 4.000 autom´viles vendidos
o A
que estar´ en servicio dentro de dos a˜os es B(4000; 0.8), luego por
a n
√ d
aproximaci´n a la normal N (np, npq), tendremos
o B
s=B+mv
3119.5 − 3200 SOCIALES
P (X 3120) =1 − P z √
640
=1 − Φ(−3.18) = Φ(3.18) = 0.9993 MaTEX
Aleatorias
Ejercicio 28
Variables
Tabla N(0,1)
Doc Doc
Volver Cerrar

75. MATEMATICAS
Soluciones a los Ejercicios 75 2º Bachillerato
r=A+lu
Ejercicio 29. A
1
El n´mero X de “seises” es de tipo B(600; ). Como se cumplen las
u d
6
condiciones n · p = √ 5 y n · q = 500 5, aproximamos por una normal
100 B
s=B+mv
con µ = 100 y σ = 83.33 = 9.13 SOCIALES
a) Obtener a lo m´s 95 –seises–
a
95.5 − 100
MaTEX
P (X ≤ 95) =P z≤
Aleatorias
9.13
Variables
=P (z ≤ −0.49) = Φ(−0.49) = 1 − Φ(0.49) = 0.3121
b) Obtener m´s de 110 –seises–
a
P (X 110) =1 − P (X ≤ 110)
110.5 − 100
=1 − P z≤
9.13
=1 − P (z ≤ 1.15) = 1 − Φ(1.15) = 0.1251
Ejercicio 29
Tabla N(0,1)
Doc Doc
Volver Cerrar

76. MATEMATICAS
Soluciones a los Tests 76 2º Bachillerato
r=A+lu
Soluciones a los Tests A
Soluci´n al Test: En efecto, X es una variable aleatoria continua el
o d
significado de FX (a) es B
s=B+mv
a SOCIALES
f (x) dx = P (X a) = P (X ≤ a)
ya que
−∞
MaTEX
Aleatorias
a
P (X ≤ a) = P (X a) + P (X = a) = P (X a) + f (x) dx = P (X a)
Variables
a
a
con f (x) dx = 0 Final del Test
a
Tabla N(0,1)
Doc Doc
Volver Cerrar

77. MATEMATICAS
2º Bachillerato
r=A+lu
A
Index
d
distribuci´n binomial, 12
o B
media, 17 s=B+mv
SOCIALES
probabilidad, 17
varianza, 17
distribuci´n normal, 26
o
MaTEX
Aleatorias
manejo de la tabla, 28
Variables
funci´n de distribuci´n, 6
o o
funci´n de probabilidad, 4
o
n´meros combinatorios, 14
u
variable aleatoria
continua, 22
discreta, 3
media, 8
varianza, 10 Tabla N(0,1)
Doc Doc
Volver Cerrar
77