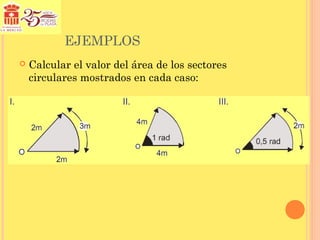
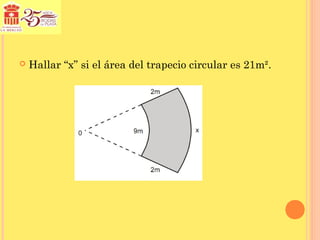
Este documento trata sobre conceptos geométricos relacionados con círculos y sectores circulares. Explica que un arco es una porción de una circunferencia y que la longitud de un arco se calcula multiplicando el radio por el ángulo central en radianes. También define el sector circular como la región delimitada por dos radios y el arco correspondiente, y que su área se calcula como la mitad del producto del radio al cuadrado por el ángulo central en radianes. Finalmente, introduce el concepto de trapecio circular.

1. ARCO Y SECTOR
CIRCULAR
Marzo, 2013.

2. ARCO DE UN SECTOR
CIRCULAR
 El Arco es una porción cualquiera de una
circunferencia.

3. LONGITUD DE ARCO
 En una circunferencia de radio “R” un ángulo
central de “π” radianes determina una longitud
de arco “L”, que se calcula multiplicando el
número de radianes “π” y el radio de la
circunferencia “R”.

4. SECTOR CIRCULAR
 Se llama sector circular a la región circular
limitada por dos radios y el arco
correspondiente.

5.  El área de un sector circular es igual al
semiproducto de la longitud de su radio elevado
al cuadrado y la medida de su ángulo central, en
radianes; es decir:

6. OTRAS FÓRMULAS

7. EJEMPLOS
 Calcular el valor del área de los sectores
circulares mostrados en cada caso:

8. OBSERVACIONES
 El incremento de un mismo radio “R” en un
sector circular inicial de área “S” (figura 1);
produce un incremento de área proporcional a los
números impares de “S”, que el estudiante
podría comprobar (figura 2).

9. ÁREA DE UN TRAPECIO
CIRCULAR
 Se llama trapecio circular a aquella región
circular formada por la diferencia de dos sectores
circulares concéntricos.

10. EJEMPLOS
 Calcular el valor del área del trapecio circular y
encontrar la medida del ángulo central en la
figura mostrada:

11.  Hallar “x” si el área del trapecio circular es 21m².

12.  De la figura mostrada, calcular el área de la
región sombreada, si el arco ABC tiene por
longitud 4π m.