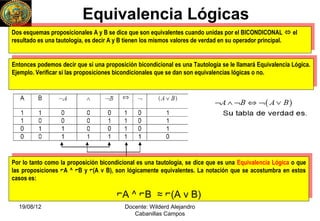
1. Equivalencia Lógicas
Dos esquemas proposicionales AA y B se dice que son equivalentes cuando unidas por el BICONDICONAL elel
Dos esquemas proposicionales y B se dice que son equivalentes cuando unidas por el BICONDICONAL 
resultado es una tautología, es decir AA y B tienen los mismos valores de verdad en su operador principal.
resultado es una tautología, es decir y B tienen los mismos valores de verdad en su operador principal.
Entonces podemos decir que sisi una proposición bicondicional es una Tautología se le llamará Equivalencia Lógica.
Entonces podemos decir que una proposición bicondicional es una Tautología se le llamará Equivalencia Lógica.
Ejemplo. Verificar sisi las proposiciones bicondicionales que se dan son equivalencias lógicas o no.
Ejemplo. Verificar las proposiciones bicondicionales que se dan son equivalencias lógicas o no.
Por lo tanto como lala proposición bicondicional es una tautología, sedice que es una Equivalencia Lógica oo que
Por lo tanto como proposición bicondicional es una tautología, se dice que es una Equivalencia Lógica que
las proposiciones ⌐A ^^⌐B y y⌐(A ν νB), son lógicamente equivalentes. La notación que se acostumbra en estos
las proposiciones ⌐A ⌐B ⌐(A B), son lógicamente equivalentes. La notación que se acostumbra en estos
casos es:
casos es:
⌐A ⌐B ≈ ⌐(A B)
⌐A ^^⌐B ≈ ⌐(A ννB)
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

2. Determinar sisi las proposiciones siguientes son
equivalentes:
Determinar las proposiciones siguientes son
equivalentes:
A= “Si “Si Juan Aprobó los exámenes
exámenes de admisión,
admisión, ingreso
A= Juan Aprobó los de a a lala ingreso
universidad”.
universidad”.
B= “No es elel caso que Juan apruebe los exámenes de admisión y y no
B= “No es caso que Juan apruebe los exámenes de admisión no
ingrese a a la universidad”
ingrese la universidad”
Solución:
Solución:
Escribiendo en forma simbólica:
Escribiendo en forma simbólica:
pp = Juan Aprobó los exámenes de admisión
= Juan Aprobó los exámenes de admisión
q = Juan ingresó a la universidad.
q = Juan ingresó a la universidad.
Entonces AA = p qq y y BB = ~(p ^ ~q)
Entonces = p  = ~(p ^ ~q)
Uniendo bicondicionalmente estos dos esquemas se tiene: (p  q) ~(p ~q)
Uniendo bicondicionalmente estos dos esquemas se tiene: (p q) ~(p ^^ ~q)
Demostrando con lala tabla de verdad:
Demostrando con tabla de verdad:
p q pq  ~(p ^ ~q)
V V V V V F
V F F V F V
F V V V V F
F F V V V F
Como en lala tabla los valores finales es una tautología las proposiciones A y B son equivalentes.
Como en tabla los valores finales es una tautología las proposiciones A y B son equivalentes.
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

3. De las siguientes proposiciones, cuáles son equivalentes:
De las siguientes proposiciones, cuáles son equivalentes:
1.1. Es necesario que Juan no estudie en lala USS para que Luis viva en Chiclayo.
Es necesario que Juan no estudie en USS para que Luis viva en Chiclayo.
2.2. No es cierto que Luis viva en Chiclayo y y que Juan estudie en lala USS.
No es cierto que Luis viva en Chiclayo que Juan estudie en USS.
3.3. Luis
Luis no no vive
vive en en Chiclayo
Chiclayo y y JuanJuan no no estudia
estudia en
en lala USS.
USS.
Solución:
Solución:
pp==Juan estudia en la USS.
Juan estudia en la USS.
qq==Luis vive en Chiclayo. Entonces:
Luis vive en Chiclayo. Entonces:
1. qq ~p
1.  ~p 2. ~(q ^^p)
2. ~(q p) 3. ~q ^^~p
3. ~q ~p
p q q  ~p  ~(q ^ p)  ~q ^ ~p
V V F V F V V F
V F V V V F F F
F V V V V F F F
F F V V V F V V
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

4. EJERCICIOS:
Simbolizar las proposición:
“Hay que cancelar 1000 soles y ser accionista para
ingresar al club” es: (p ∧q) → r
Pagar 1000 soles o ser accionista y no ingresar al
club. (p v q) ∧ ∼r
Pagar 1000 soles y ser accionista o no ingresar al club.
( p ∧ q) v ∼r
Pagar 1000 soles y no ser accionista y estar en el club.
( p ∧ ∼q) ∧ r
DETERMINAR CUAL DE LOS ESQUEMAS ANTERIORES SON EQUIVALENTES
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

5. Desarrollar:
1) ~(p q)  ~[ (~q)  (~p) ]
2)[ p  (q r ) ]  [ (p ^ ~r )  ~q]
3)[(~p ^ q) r ]  [r ^ ~(p ν~q)]
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

6. LEYES DE LA EQUIVALENCIA LÓGICA
Las leyes de equivalencias más conocidas son:
A. Ley de la Doble Negación: ∼∼p ≡ p
B. Ley de Idempotencia de la Conjunción y la Disyunción:
p∧p≡p
p∨p≡p
C. Leyes Conmutativas:
p∧q≡q∧p
p∨q≡q∨p
p↔q≡q↔p
D. Leyes Asociativas:
(p ∧ q) ∧ r ≡ p ∧ (q ∧ r)
(p ∨ q) ∨ r ≡ p ∨ (q ∨ r)
(p ↔ q) ↔ r ≡ p ↔ (q ↔ r)
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

7. E. Leyes Distributivas:
p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
p→ (q ∨ r) ≡ (p → q) ∨ (p → r)
p→ (q ∧ r) ≡ (p → q) ∧ (p → r)
F. Leyes de Identidad:
p∧V≡p
p∨F≡p
p∧F≡F
p∨V≡V
G. Leyes de D`Morgan:
∼(p ∧ q) ≡ (∼p ∨ ∼q)
∼(p ∨ q) ≡ (∼p ∧ ∼q)
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

8. H. Leyes de la Absorción:
p ∧ (p ∨ q) ≡ p
p ∧ (∼p ∨ q) ≡ p ∧ q
p ∨ (p ∧ q) ≡ p
p ∨ (∼p ∧ q) ≡ p∨ q
I. Leyes del Condicional:
p → q ≡ ∼p ∨ q
∼(p → q) ≡ p ∧ ∼q
J. Leyes del Bicondicional:
p ↔ q ≡ (p→ q) ∧ (q→ p)
p ↔ q ≡ (p ∧ q) ∨ (∼p ∧ ∼q) ≡ ∼(p ∆ q)
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

9. OBSERVACIÓN:
K. Leyes de Contraposición: Estas leyes
p → q ≡ ∼q → ∼p permiten la
p ↔ q ≡ ∼q ↔ ∼p transformación y
L. Leyes de Exportación: simplificación de
(p ∧ q) → r ≡ p → (q → r) un esquema
molecular en otro
M. Ley del Tercio Excluido: más simple,
∼p ∨ p ≡ V cambiando una o
N. Ley de la Contradicción: más expresiones
∼p ∧ p ≡ F componentes del
O. Reducción al Absurdo: esquema por sus
p → q ≡ (p ∧ ∼q) → F equivalentes
lógicos.
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

10. Ejemplos:
b) Simplificar: [∼(p → q) ∧ (∼q ∨ p)] ∨ p
Tenemos:
[∼ (∼p ∨ q) ∧ (∼q ∨ p)] ∨ p Condicional
[(∼∼p ∧ ∼q) ∧ (∼q ∨ p)] ∨ p Morgan
{p ∧ ∼q ∧ (∼q ∨ p)} ∨ p Doble negación
(p ∧ ∼q) ∨ p Absorción
p ∨ (p ∧ ∼q) Conmutativa
p Absorción
Luego: [∼(p→ q) ∧ (∼q ∨ p)] ∨ p ≡ p
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

11. a) Simplificar el esquema: ∼(p ↔ q) ∨ (∼p → q)
Tenemos:
∼[(p ∧ q) ∨ (∼p ∧ ∼q)] ∨ (∼∼p ∨ q) Bicondicional y condicional
[∼(p ∧ q) ∧ ∼(∼p ∧ ∼ q)] ∨ (p ∨ q) Morgan
[(∼p ∨ ∼q) ∧ (∼∼p ∨ ∼∼q)] ∨ (p ∨ q) Morgan
[(∼p ∨ ∼ q) ∧ (p ∨ q)] ∨ (p ∨ q) Doble negación
(p ∨ q) ∨ [(p ∨ q) ∧ (∼p ∨ ∼ q) Conmutativa
(p ∨ q) Absorción
Por lo tanto: ∼(p ↔ q) ∨ (∼p→ q) ≡ (p ∨ q)
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

12. ¿QUÉ ES UN ARGUMENTO?
Un argumento es una proposición compuesta del tipo
Si (p1 ∧ p2 ∧ p3 ∧ ..... ∧ pk) entonces q
Premisas → Conclusión
Ejemplo
Si Roxana gana la beca, estudiará en la Universidad Señor de Sipan. Y Roxana
ganó la beca.
Por lo tanto, estudiará en la Universidad Señor de Sipan.
Este argumento tiene dos premisas.
Las premisas son: “Si Roxana gana la beca entonces estudiará en la
Universidad Señor de Sipan” y “ Roxana se ganó la beca”.
La conclusión es: “Roxana estudiará en la Universidad Señor de Sipan”.
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

13. ¿QUÉ ES UNA IMPLICACIÓN?
La implicación lógica es la relación entre dos formulas proposicionales a través
del conectivo lógico CONDICONAL y cuyo resultado es una tautología
Ejemplos: Determinar la validez de la siguiente implicación
[(p ^ ~q) ^ (~p r)]  (p ν ~q)
p q r [(p ^ ~q) ^ (~p r)]  (p ν ~q)
V V V V F F F F F V V V V F
V V F V F F F F V F V V V F
V F V V V V F F F V V V V V
V F F V V V V F V F V V V V
F V V F F F F V V V V F F F
F V F F F F F V F F V F F F
F F V F F V F V V V V F V V
F F F F F V F V F F V F V V
El resultado del esquema molecular es una tautología por lo tanto es una implicación
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

14. LA INFERENCIA LÓGICA
La Inferencia: Es un proceso mental lógico de pasar de un conjunto de
proposiciones llamadas premisas a una conclusión y suele indicarse a través
de expresiones como: Luego, en consecuencia, por lo tanto, por consiguiente
etc. Existen dos tipos de inferencias.
•La Inferencia inmediata: Se caracteriza porque la conclusión se
desprende o deriva sobre la base de una sola premisa.
Ejemplo:
Toda papaya es fruta
Alguna fruta es papaya
•La inferencia mediata: Se caracteriza porque la conclusión se deriva de
dos o más premisas.
Ejemplo:
Todo contador conoce la elaboración de un balance económico
José es contador
José conoce la elaboración de un balance económico
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

15. Las inferencias lógicas son implicaciones o condicionales de forma:
Horizontal Vertical
p1 ∧ p2 ∧ …. ∧ pm ⇒ q p1 p2
pm
∴q
Donde: p1, p2, p3…, pm representan a cada una de las premisas y “q” es la conclusión
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

16. El Método abreviado
Cuando el número de variables pasa de tres se torna tedioso el
método de la tabla de verdad; para contrarrestar este
inconveniente se utiliza el método abreviado cuyo procedimiento
consiste.
•Suponer que en la condicional: el antecedente es verdadero y el
consecuente es falso.
•Determinar los valores de las variables del consecuente de
manera que expresen la falsedad de este.
•Reemplazar en el antecedente los valores obtenidos del
consecuente, para encontrar los valores de las demás variables.
•Si se verifica la estructura de la condicional con dichos valores la
inferencia es inválida, sin embargo, si obtenemos una proposición
simple con dos valores de verdad se concluye que es una
contradicción y por lo tanto la inferencia será válida.
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

17. Ejemplo:
Si la tormenta continúa, nos quedaremos en casa; si nos quedamos en casa, no
iremos al concierto. Luego si la tormenta continúa no iremos al concierto.
Fórmula p: La tormenta continúa (p → q)
q: nos quedamos en casa q→ ∼r
r : iremos al concierto _______
p→ ∼r
[( p → q) ∧ ( q → ∼ r) ] → (p → ∼ r)
V → F
* p → ∼ r ≡ F ; V (p) ≡ V V ( r) ≡ V
* p → q ≡ V ; V (p) ≡ V V ( q) ≡ V
* q → ∼ r ≡ V ; V (q) ≡ V V ( r) ≡ F
Observamos que r tiene dos valores luego la inferencia es válida.
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

18. INFERENCIA LÓGICA
Si de una oomas proposiciones llamadas premisas, se deduce lalaafirmación de una proposición, llamada
Si de una mas proposiciones llamadas premisas, se deduce afirmación de una proposición, llamada
conclusión se dice que se ha construido una inferencia.
conclusión se dice que se ha construido una inferencia.
Ejemplos: Determinar sisi p ν q es una consecuencia valida de:
Ejemplos: Determinar p ν q es una consecuencia valida de:
~p  ~q, ~q  r,r,
~q 
~p  ~q, ~~ r
r
p q r ( ~p  ~q ) ^ (~q  r) ^ (~r)  ( p ν q)
V V V V V V F F V V
V V F V V V V V V V
V F V V V V F F V V
V F F V F F F V V V
F V V F F V F F V V
F V F F F V F V V V
F F V V V V F F V F
F F F V F F F V V F
1 3 2 5 4 7 6
Como elel resultado es una tautología la inferencia es valida
Como resultado es una tautología la inferencia es valida
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

19. Determinar lala validez de la inferencia siguiente:
Determinar validez de la inferencia siguiente:
Sí elel triángulo es isósceles entonces tiene dos lados iguales. Pero el triángulo no tiene dos lados
Sí triángulo es isósceles entonces tiene dos lados iguales. Pero el triángulo no tiene dos lados
iguales: por lo tanto no es isósceles.
iguales: por lo tanto no es isósceles.
Solución:
Solución:
p= El triángulo es isósceles.
p= El triángulo es isósceles.
q= El triángulo tiene dos lados iguales.
q= El triángulo tiene dos lados iguales.
El esquema de lala inferencia sería: [(p q) ^^ (~q) ] (~p)
El esquema de inferencia sería: [(p  q) (~q) ]  (~p)
p q ( p  q ) ^ (~q)  (~p)
V V V F F V F
V F F F V V F
F V V F F V V
F F V V V V V
1 3 2 5 4
Como el resultado es una tautología la inferencia es valida
Como el resultado es una tautología la inferencia es valida
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

20. EJEMPLOS
Si llovió entonces hubo nubes. No hubo nubes, por tanto, no llovió.
La simbolización es: Luego, la simbolización completa es:
p = llovió y p→ q
q =hubo nubes ~q
~p
p q ( p → q) ^ ~q → ~p
V V V F F V F
V F F F V V F
F V V F F V V
F F V V V V V
1 3 2 5 4
Como el resultado es una tautología la inferencia es valida
Como el resultado es una tautología la inferencia es valida
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

21. Si se levanta aire húmedo, entonces refrescará. Si refresca entonces se formarán
nubes, no se levanta aire húmedo. Por tanto, no se formarán nubes.
La simbolización es: Luego, la simbolización completa es:
p= Se levanta aire húmedo y p→q
q=refrescará q→r
r=se formarán nubes. ~p
~r
p q r [ (p → q) ^ (q → r) ] ^ ~p → ~r
V V V V V V F F V F
V V F V F F F F V V
V F V F F V F F V F
V F F F F V F F V V
F V V V V V V V F F
F V F V F F F V V V
F F V V V V V V F F
F F F V V V V V V V
1 3 2 5 4 7 6
Como el resultado no es una tautología la inferencia no es valida
Como el resultado no es una tautología la inferencia no es valida
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

22. El amor es ciego y los hombres no son conscientes del hecho de que el amor es ciego, o el amor es
ciego y las mujeres sacan ventaja de ello. Si los hombres no son conscientes de que el amor es ciego,
entonces el amor no es ciego. En conclusión, las mujeres sacan ventaja de ello.
Amor ciego: p
Hombres no conscientes: ~ q
Mujeres sacan ventaja: r
FORMALIZAMOS: ((p ^ ~q) v (p ^ r)) ^(~q → ~p) →r
P q r ((p ^ ~ q) v (p ^ r)) ^ (~ q → ~ p) → r
V V V V F F V V V V V V F V V F V V V
V V F V F F V F V F F F F V V F V V F
V F V V V V F V V V V F V F F F V V V
V F F V V V F V V F F F V F F F V V F
F V V F F F V F F F V F F V V V F V V
F V F F F F V F F F F F F V V V F V F
F F V F F V F F F F V F V F V V F V V
F F F F F V F F F F F F V F V V F V F
Como el resultado es una tautología la inferencia es valida
Como el resultado es una tautología la inferencia es valida
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

23. Cuando Eduardo no juega al baloncesto, juega al tenis;
cuando juega al tenis, juega al fútbol; no juega al fútbol. Por tanto, Eduardo juega al
baloncesto.
Eduardo juega baloncesto: p
Eduardo juega tenis: q
Eduardo juega fútbol: r
FORMALIZAMOS: ((~p → q) ^ (q → r)) ^ ~r → p
p q r ((~ p → q) ^ (q → r)) ^ ~ r → p
V V V F V V V V V V V F F V V V
V V F F V V V F V F F F V F V V
V F V F V V F V F V V F F V V V
V F F F V V F V F V F V V F V V
F V V V F V V V V V V F F V V F
F V F V F V V F V F F F V F V F
F F V V F F F F F V V F F V V F
F F F V F F F F F V F F V F V F
Como el resultado es una tautología la inferencia es valida
Como el resultado es una tautología la inferencia es valida
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

24. Resolver: Traducir a forma simbólica y comprobar la validez
de los enunciados.
1. Si usted gana el premio mayor, entonces se hará millonario. Se hace
usted millonario, entonces podrá vivir mejor. Usted gana el premio
mayor luego: p. : gana el premio mayor q. : es millonario r. : podré vivir mejor.
{[(p → q) ^ (q → r)] ^ p} → r
2. Si la enfermedad del paciente tiene un diagnóstico de tuberculosis
,entonces la bacteria que posee es el bacilo de Koch .Se sabe que la
bacteria que posee no es bacilo de Koch. En consecuencia.
p. : la enfermedad tiene un diagnóstico de tuberculosis q. : la bacteria es el bacilo de Koch.
[(p → q) ^ ~ q ] → ~ p
3. El argumento: Eres Ingeniero o Matemático. Pero no eres
profesional en matemáticas. Por tanto: eres profesional en Ingeniería
[(p v q) ^ ~ q] → p
4. La proposición Si caigo, ve que camino Si me levanto, camino. Por
ya que caigo bien se
me levanto.
tanto.
p : Me caigo q : Me levanto r : camino [(p → q) ^ (q → r) ] → (p → r)
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

25. Reglas de Inferencia.
Cuando aparecen tres o más proposiciones simples en
un argumento resulta tedioso estar utilizando las tablas
de verdad para verificar su valides, existe un método
más conveniente para verificar si un argumento es
válido o no, es deducir las conclusiones de sus
premisas por una secuencia de argumentos más
cortos y más elementales que sabemos válidos. A
estos nuevos argumentos más cortos, que son válidos,
se les llama Reglas de Inferencia.
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

26. Modus Ponendo Ponens
Esta regla de inferencia se aplica cuando aparecen como premisas
una condicional y el antecedente de esa condicional para obtener
como conclusión al consecuente de la condicional. Consideremos
algunos ejemplos en donde se aplica la regla de Inferencia del
Modus Ponendo Pones.
Ejm. Nº1
Si estudio mucho, entonces pasaré el examen….premisa 1 A B P1
Estudio mucho…………………………………………premisa 2 A P2
Pasaré el examen……………………………………...conclusión. B Conclusión
Ejm. Nº2
Si no hace frió, entonces el lago no se helará….premisa 1 ⌐C  ⌐ D P1
No hace frió……………………………………………premisa 2
El lago no se helará………………………………….conclusión ⌐C P2
⌐ D Conclusión
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

27. Modus Tollendo Tollens
Esta regla de inferencia se aplica cuando se tiene como premisas a
una proposición condicional y como otra de las premisas a la
negación del consecuente de la condicional, para obtener como
conclusión la negación del antecedente.
Si llovió entonces hubo nubes………….…premisa 1 A B P1
⌐B P2
No hubo nubes………………………… …premisa 2 ⌐ A Concusión
No llovió………………………………… …. conclusión.
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

28. Regla de Adjunción
Esta regla será denotada con “A” y consiste en lo siguiente.
Supongamos que se tienen las proposiciones verdaderas:
Cinco es mayor que tres
Y la segunda es:
Tres es menor que cuatro
Como ambas son verdaderas, entonces también lo es la
proposición:
Cinco es mayor que tres y tres es menor que cuatro
Al simbolizar las proposiciones se tiene lo siguientes:
A P1
B P2 A ^ B Conclusión
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

29. Regla de Simplificación
Esta regla la denotaremos con “S” y es recíproca a la anterior,
es decir, si se tiene la proposición verdadera:
Cinco es mayor que tres y tres es menor que cuatro
Podemos deducir las proposiciones verdaderas:
La primera de ellas es: cinco es mayor que tres
Y la segunda es: tres es menor que cuatro
Ahora al simbolizar las proposiciones se tiene:
A^B P1
A Conclusión
B Conclusión
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

30. Ley de Silogismo Hipotético
La abreviatura que utilizaremos es “S.H.” y si se tienen las
premisas:
Si voy a la Universidad entonces asisto a clases
Si asisto a clases entonces entiendo los temas
Al utilizar la Ley del Silogismo Hipotético concluimos:
Si voy a la Universidad entonces entiendo los temas
Al simbolizar estas proposiciones se tiene lo siguiente:
A=voy a la Universidad B=asisto a clases y C=entiendo los temas.
Luego la simbolización completa es:
AB P1
BC P2
AC Conclusión
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

31. Ley de Silogismo Disyuntivo
Esta ley afirma:
Sí se niega uno de los miembros de una premisa disyuntiva,
se concluye en la afirmación del otro miembro.
Ejemplo:
X es número par o múltiplo de 5……..p v q
X no es par……………………………. ~p
X es múltiplo de 5………………….. q ó
X es número par o múltiplo de 5……..p v q
X no es múltiplo de 5.………………. ~q
X es par………………………….……. p
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos

32. Reglas de Inferencia
Nombre de la Regla Implicación lógica
Simplificación (p ∧ q) ⇒ p
Amplificación p ⇒ (p∨ q)
Modus Ponens [ p ∧ ( p → q)] ⇒ q
Modus Tollens [( p → q) ∧ ¬q ] ⇒ ¬p
Silogismo hipotético [(p → q) ∧ (q → r)] ⇒ (p → r)
Silogismo disyuntivo [( p ∨ q) ∧ ¬p)] ⇒ q
Reducción (p ∧ q) = p
(p ∧ q) = q
19/08/12 Docente: Wilderd Alejandro
Cabanillas Campos