Sexto 4
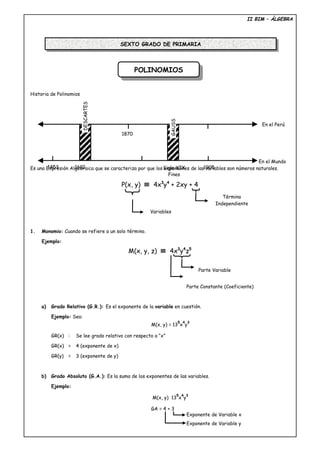
- 1. POLINOMIOSPOLINOMIOS II BIM – ÁLGEBRA Historia de Polinomios Es una Expresión Algebraica que se caracteriza por que los exponentes de las variables son números naturales. P(x, y) ≡ 4x3 y4 + 2xy + 4 1. Monomio: Cuando se refiere a un solo término. Ejemplo: M(x, y, z) ≡ 4x3 y4 z5 a) Grado Relativo (G.R.): Es el exponente de la variable en cuestión. Ejemplo: Sea: M(x, y) = 13 5 x 4 y 3 GR(x) : Se lee grado relativo con respecto a “x” GR(x) = 4 (exponente de x) GR(y) = 3 (exponente de y) b) Grado Absoluto (G.A.): Es la suma de los exponentes de las variables. Ejemplo: M(x, y) 13 5 x 4 y 3 GA = 4 + 3 SEXTO GRADO DE PRIMARIA 1870 1453 1610 1905 En el Perú En el Mundo Siglo XIX Fines DESCARTES GAUSS Término Independiente Variables Parte Variable Parte Constante (Coeficiente) Exponente de Variable x Exponente de Variable y
- 2. II BIM – ÁLGEBRA GA = 7 Monomio M(x, y, z) Parte Constante (Coeficiente) Parte Variable GA GR(x) GR(y) GR(z) 39x 3 y -4 zx3– 4 5x 2 yz 3 18z -4x 5 y 4 8 2. Polinomio: Es la agrupación por adición de monomios no semejantes. Ejemplo: P(x; y) ≡ 2xy3 + 4y4 – 3x + 2 Polinomio de 4 términos P(x) = x 4 + x 3 – x 2 + 2x + 3 Polinomio de ________________ P(y) = ax 2 + bx + c Polinomio de ________________ P(x; y) = x + y Polinomio de ________________ ( ) a) Grado Relativo (G.R.): Se calcula el grado relativo de la variable en cuestión de cada monomio y se toma el mayor grado relativo como grado relativo de dicha variable en el polinomio. P(x; y) = 2x3 y4 + 5x5 y3 + 2xy2 Entonces: GR (x) = 5 GR(y) = 4 AHORA TU: P(x, y) ≡ 3x 3 y + 2xy + 4x 2 y – x 5 y GR(x) = GR(y) = b) Grado Absoluto (G.A.): De la misma manera se calcula en cada monomio el GA y se toma al mayor. P(x; y) = 2x3 y4 + 5x5 y3 + 2xy2 ⇒ GA = 8 Término Independiente GR(x) = 3 GR(y) = 4 GR(x) = 5 GR(y) = 3 GR(x) = 1 GR(y) = 2 GA = 7 GA = 8 GA = 3
- 3. II BIM – ÁLGEBRA ¡AHORA! P(x, y) ≡ 3x 3 y + 2xy + 4xy 2 – x 5 y GA. = Polinomio P(x, y, z) GA GR(x) GR(y) GR(z) x 6 + xy + x 3 y 4 z x + y + z zxy + x 2 y 3 + 4 a + abx + bx 2 3x 3 + 4y 4 -x 3 y 4 + x 5 + y 8 4z 3 + 4z – 3 VALOR NUMÉRICO Cuando mas variables adoptan un valor, los monomios o polinomios arrojan un valor que se denomina valor numérico. Ejemplo: P(x) = 4x + 14 → P(1) = 4 . 1 + 14 = 18 P(1) = 18 → P(2) = 4 . 2 + 14 = 22 P(2) = 22 → P(3) = 4 . 3 + 14 = 26 P(3) = 26 → M(x; y) = 4x 2 y 3 ↓ ↓ M(2, 1) ⇒ x = 2 y = 1 M(2, 1) = 4(2) 2 (1) 3 M(2, 1) = 16 → P(x, y) = 4x + 5xy ↓ ↓ P(2, 3) x = 2 y = 3 P(2, 3) = 4(2) + 5(2)(3) P(2, 3) = 38 ¡AHORA TU! P(x, y) = 4xy + 2x 2 y P(2, 1) = P(1, 2) = P(1, 1) = M(x) = 4x M(2) = M(3) = M(4) =
- 4. II BIM – ÁLGEBRA 1. Dado el monomio: M(x, y) = -3abx a+3 y b De GR(x) = 7 y GA = 10 Calcular: El coeficiente a) -36 b) 36 c) 12 d) -12 e) N.A. 2. Si el siguiente monomio: M(x, y, z) = -4x a+1 y b+2 z 4 Es de GA = 14 y GR(y) = GR(z) Calcular: “a . b” a) 15 b) 10 c) 5 d) 3 e) 6 3. Si el monomio: M(a; b) = -4xya x+2 b y+5 Donde GR(a) = 5 GR(b) = 7 Calcular: “El coeficiente” a) 24 b) -24 c) 25 d) 26 e) 12 4. Si en el monomio: M(w, t, ψ) = -2a 2 b 3 w a+3 t b+2 ψ 6 El GA = 17 y GR(w) = 5 Calcular: “El coeficiente” a) 512 b) 251 c) -512 d) 251 e) 521 5. Si: GA = 15 2 3 )y(GR 2 )z(GR )x(GR === De: M(x, y, z) = -4x a y b+2 z c+3 Calcular: 7 cba A ++ = a) 5 b) 4 c) 3 d) 2 e) 1 6. Si: GA = 10; GR(x) = 5 del polinomio: P(x, y) = 4x a+1 y b + 5x a+2 y b+1 + 3x a y b+2 Calcular: A = a + b a) 1 b) 2 c) 3 d) 4 e) N.A. 7. Dado el polinomio: P(x, y) = x a y b+2 + x a+1 y b+4 + x a+5 y b + ab Si: GR(x) = 7 GR(y) = 6 Calcular el término independiente: a) 5 b) 6 c) 7 d) 12 e) N.A. 8. Si: P(x, y) = ax a+b y c+2 + bx a+b+1 y c+3 + cx a+b+3 y c + abc Es de GR(x) = 14 GR (y) = 6 Calcular la suma de coeficientes: a) 3 b) 4 c) 5 d) 7 e) N.A. 9. Si: P(x, y, z) = x a y b z c + x a+1 y b+1 z c-1 + x a + 2y b - 2z c Donde: GA(x) = 4 GR(y) = 5 GR(z) = 3 Calcular el grado absoluto. EJERCICIOS DE APLICACIÓNEJERCICIOS DE APLICACIÓN
- 5. II BIM – ÁLGEBRA Rpta.: __________________ 10. Dado el polinomio: P(x) = x a+3 + x a+4 + x a+2 + 2a Calcular el término independiente si GA = 8. Rpta.: __________________ 11. Calcular “A” Si: M(x) = 2x 4 Si: )1(M )2(M)0(M A + = Rpta.: __________________ 12. Calcular: P(7) Si: P(x) = -x 5 + 7x 4 + 2x – 10 Rpta.: __________________ 13. Si: P(x) = 2x + 4 Calcular: M = P (P (P (P ( 3 ) ) ) ) Rpta.: __________________ 14. Si: P(x) = 2x – 1 Q(x) = x + 3 Calcular: P(Q(x)) Rpta.: __________________ 15. Si: P(x) = x + 5 Q(x) = x + 2 Calcular: P(Q(x)) Rpta.: __________________ TAREA DOMICILIARIA 1. Dado el monomio: M(x, y) = 4abx a y b Si: GR(x) = 2 GA = 7 Calcular: “El Coeficiente” a) 10 b) 20 c) 30 d) 40 e) 50 2. En el siguiente monomio: M(x, y, z) = 3x m+1 y p+2 z 2 GA = 12 GR(x) = GR(y) Calcular: m . P a) 12 b) 13 c) 14 d) 15 e) 16 3. Si el monomio: M(ψ,θ) = 2xyψ x+4 θ y+2 Donde: GR(ψ) = 7 GR(θ) = 5 Calcular el coeficiente: a) 18 b) 19 c) 20 d) 21 e) 24 4. Si el monomio: M(x, y, z) = 2a 2 b 3 c 4 x a+5 y b+4 z c+3 Si: GA = 15 GR(x) = 6 GR(z) = 4 Calcular el coeficiente: a) 2 b) 4 c) 5
- 6. II BIM – ÁLGEBRA d) 16 e) 14 5. Si: GA = 24 5 )x(GR )y(GR = M(x, y) = 2x a+b y a-b Calcular: a . b a) 96 b) 108 c) 64 d) 25 e) 15 6. Si: P(x) = x a+4 + x a+3 + x a-4 GA = 7 Calcular : a3 a) 3 b) 4 c) 5 d) 6 e) 7 7. Si : P(x, y) = 2x a+1 y b-1 + x a+3 y b-4 + x a+2 y b-2 GR(x) = 5 GR(y) = 3 Calcular el GA a) 1 b) 2 c) 3 d) 4 e) N.A. 8. Si: P(x) = ax a + (a + 1)x a+1 + (a + 2)x a-4 Es de GA = 5 Calcular la suma de coeficientes: a) 14 b) 15 c) 16 d) 17 e) 18 9. P(x, y, z) = x a y b z c + x a+1 y b+1 z c-1 + x a y b z c GR(x) = 4 GR(y) = 5 GR(z) = 3 Calcular el grado absoluto. a) 1 b) 14 c) 12 d) 10 e) N.A. 10. Dado el polinomio: P(x, y) = x a y b + x a+1 y b+2 + x a+3 y b-3 Si el GA = 7 Además a – b = 2 Calcular: A = a b a) 1 b) 2 c) 3 d) 4 e) 5
- 7. II BIM – ÁLGEBRA d) 16 e) 14 5. Si: GA = 24 5 )x(GR )y(GR = M(x, y) = 2x a+b y a-b Calcular: a . b a) 96 b) 108 c) 64 d) 25 e) 15 6. Si: P(x) = x a+4 + x a+3 + x a-4 GA = 7 Calcular : a3 a) 3 b) 4 c) 5 d) 6 e) 7 7. Si : P(x, y) = 2x a+1 y b-1 + x a+3 y b-4 + x a+2 y b-2 GR(x) = 5 GR(y) = 3 Calcular el GA a) 1 b) 2 c) 3 d) 4 e) N.A. 8. Si: P(x) = ax a + (a + 1)x a+1 + (a + 2)x a-4 Es de GA = 5 Calcular la suma de coeficientes: a) 14 b) 15 c) 16 d) 17 e) 18 9. P(x, y, z) = x a y b z c + x a+1 y b+1 z c-1 + x a y b z c GR(x) = 4 GR(y) = 5 GR(z) = 3 Calcular el grado absoluto. a) 1 b) 14 c) 12 d) 10 e) N.A. 10. Dado el polinomio: P(x, y) = x a y b + x a+1 y b+2 + x a+3 y b-3 Si el GA = 7 Además a – b = 2 Calcular: A = a b a) 1 b) 2 c) 3 d) 4 e) 5
