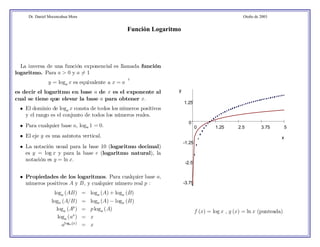
Este documento explica las funciones logarítmicas. Define la función logarítmica como la inversa de una función exponencial, donde el logaritmo en base a de x es el exponente al que se debe elevar a para obtener x. Detalla que el dominio de una función logarítmica son los números positivos y el rango son los números reales, y que para cualquier base a, loga1 = 0. También enumera algunas propiedades clave de los logaritmos, como que loga(AB) = loga(A) + loga(B).

1. Dr. Daniel Mocencahua Mora Otoño de 2003
La inversa de una función exponencial es llamada función
logaritmo. Para a > 0 y a6= 1
y = loga x es equivalente a x = ax
es decir el logaritmo en base a de x es el exponente al
cual se tiene que elevar la base a para obtener x.
• El dominio de loga x consta de todos los números positivos
y el rango es el conjunto de todos los números reales.
• Para cualquier base a, loga1 = 0.
• El eje y es una asíntota vertical.
• La notación usual para la base 10 (logaritmo decimal)
es y = logx y para la base e (logaritmo natural), la
notación es y = lnx.
• Propiedades de los logaritmos. Para cualquier base a,
números positivos A y B, y cualquier número real p :
loga (AB) = loga
(A)+ loga (B)
loga (A/B) = loga
(A) − loga (B)
loga (Ap) = p loga (A)
loga (ax) = x
aloga(x) = x
0 1.25 2.5 3.75 5
1.25
0
-1.25
-2.5
-3.75
x
y
f (x) = log x , g (x) = lnx (punteada)
Función Logaritmo
y