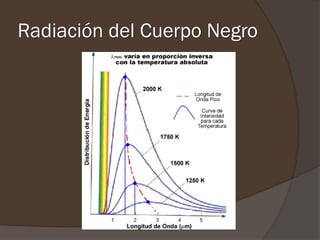
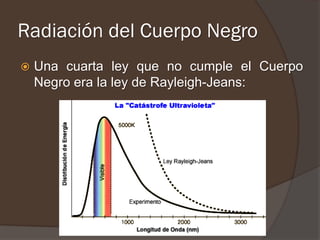
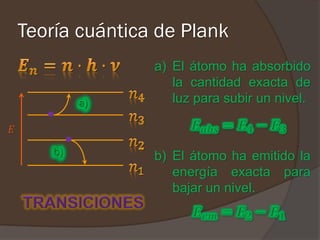
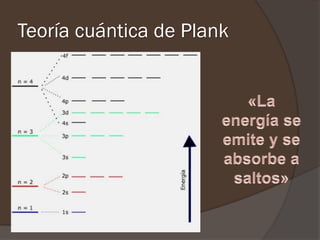
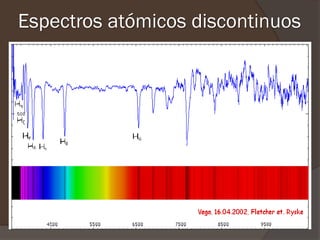
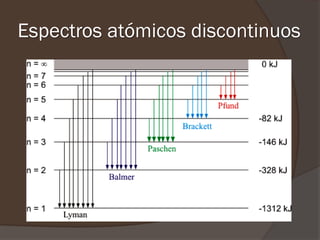
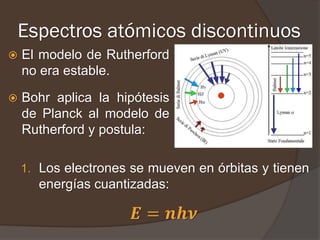
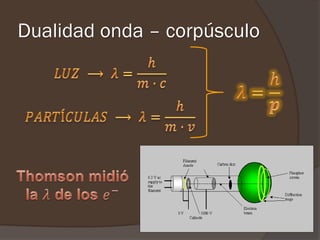
El documento describe la radiación del cuerpo negro y las leyes que lo rigen. Explica la teoría cuántica de Planck y cómo resolvió problemas con las leyes previas mediante la hipótesis de que la energía de los osciladores atómicos está cuantizada. También cubre efectos como el fotoeléctrico y cómo Einstein los explicó usando la naturaleza cuántica de la luz.

1. TEMA 10

2. Radiación del Cuerpo Negro

3. Radiación del Cuerpo Negro
 Todos los cuerpos emiten energía
electromagnética de diferentes longitudes de
onda en función de su temperatura.
 A esta energía se la llama radiación térmica.
 Cuerpo negro: absorbe toda la radiación que
entra en el.
 El cuerpo negro cumple tres leyes deducidas
de las leyes de Maxwell y de la termodinámica.

4. Radiación del Cuerpo Negro
1. Ley de Kirchhoff:

5. Radiación del Cuerpo Negro
2. Ley de desplazamiento de Wien

6. Radiación del Cuerpo Negro

7. Radiación del Cuerpo Negro
3. Ley de Stefan – Boltzman

8. Radiación del Cuerpo Negro
 Una cuarta ley que no cumple el Cuerpo
Negro era la ley de Rayleigh-Jeans:

9. Teoría cuántica de Plank

10. Teoría cuántica de Plank
 Propuso que cada átomo del cuerpo negro
oscilaba con una frecuencia 𝜈 característica
y propuso una hipótesis:

11. Teoría cuántica de Plank
 La energía de los osciladores atómicos está
cuantizada.
 La energía emitida por un cuerpo es un
múltiplo entero de CUANTOS (valor mínimo
de energía).

12. Teoría cuántica de Plank
a) El átomo ha absorbido
la cantidad exacta de
luz para subir un nivel.
𝐸
b) El átomo ha emitido la
energía exacta para
bajar un nivel.

13. Teoría cuántica de Plank

14.  Halla el intervalo de energía, en eV,
correspondiente al espectro visible.
 Datos:
 𝜆 𝑟𝑜𝑗𝑜 = 760 𝑛𝑚
 𝜆 𝑣𝑖𝑜𝑙𝑒𝑡𝑎 = 380 𝑛𝑚
 ℎ = 6′ 63 · 10−34 𝐽 · 𝑠
 𝑐 = 3 · 108 𝑚/𝑠
 1 𝑒𝑉 = 1′ 602 · 10−19 𝐽

15.  Aplicamos la hipótesis de Planck:
Δ𝐸 = 𝐸 𝑣𝑖𝑜𝑙𝑒𝑡𝑎 − 𝐸 𝑟𝑜𝑗𝑜 = ℎ𝜈 𝑣𝑖𝑜𝑙𝑒𝑡𝑎 − ℎ𝜈 𝑟𝑜𝑗𝑜
𝑐 𝑐 1 1
Δ𝐸 = ℎ − =ℎ· 𝑐 −
𝜆𝑣 𝜆𝑟 𝜆𝑣 𝜆𝑟
𝑚 1 1
Δ𝐸 = 6′ 63 · 10−34 𝐽· 𝑠·3 · 108 · ′ −7 𝑚
− ′
𝑠 3 8 · 10 7 6 · 10−7 𝑚
Δ𝐸 = 2′ 61 · 10−19 𝐽 = 1′ 64 𝑒𝑉

16. Efecto fotoeléctrico

17. Efecto fotoeléctrico
 Hertz publicó en 1887 que una lámina de zinc
iluminada con uv emitía partículas.
 ¡¡¡nada más demostrar que la luz es una onda
se publica un experimento en el que la luz se
comporta como una partícula!!!

18. Efecto fotoeléctrico
 Para determinar la 𝐸 𝑐 máxima con la que
salen los electrones se busca el valor del
potencial que es capaz de frenarlos:
«potencial de frenado».
 Si aumentamos la intensidad de la luz
aumenta el nº de 𝑒 − emitidos por unidad de
tiempo, pero no su velocidad.

19. Efecto fotoeléctrico
 Si disminuimos la frecuencia de la luz
incidente disminuye la energía de los 𝑒 −
arrancados al metal.
 Por debajo de una «frecuencia umbral 𝜈0 » no
se desprende ningún 𝑒 − . Para cada metal
existe una 𝜈0 característica.

20. Efecto fotoeléctrico
 En 1905, Einstein soluciona parte del
problema:

21. Efecto fotoeléctrico
 Conclusiones:
1. La luz está cuantizada y su energía
depende de la frecuencia de radiación y no
de su intensidad.
2. En el efecto fotoeléctrico, la energía máxima
de los 𝑒 − es directamente proporcional a la
frecuencia de la luz incidente.

22.  La frecuencia umbral del potasio es de
5′ 3 · 1014 𝑠 −1 .
 ¿Cuál es el potencial de frenado de los
electrones si se utiliza una luz de frecuencia
7′ 5 · 1014 𝐻𝑧?
 ℎ = 6′ 63 · 10−34 𝐽 · 𝑠
 𝑒 = −1′ 60 · 10−19 𝐶

23.  Aplicamos la ecuación del efecto fotoeléctrico:
ℎ𝜈 = 𝑊 + 𝐸 𝑐 = ℎ𝜈0 + 𝑞𝑉
ℎ 𝜈 − 𝜈0
𝑉=
𝑞
6′ 63 · 10−34 𝐽 · 𝑠 7′ 5 · 1014 𝐻𝑧 − 5′ 3 · 1014 𝐻𝑧
𝑉=
−1′ 60 · 10−19 𝐶
𝑉 = −0′ 912 𝑉

24. Espectros atómicos discontinuos

25. Espectros atómicos discontinuos
 Explicación de Balmer y Rydberg:
𝑅 = 1′ 09677 · 107 𝑚−1
1 1 1
= 𝑅 2− 2
𝜆 𝑛1 𝑛2

26. Espectros atómicos discontinuos

27. Espectros atómicos discontinuos
 El modelo de Rutherford
no era estable.
 Bohr aplica la hipótesis
de Planck al modelo de
Rutherford y postula:
1. Los electrones se mueven en órbitas y tienen
energías cuantizadas:
𝑬 = 𝒏𝒉𝝂

28. Espectros atómicos discontinuos
2. Sólo están permitidas aquellas órbitas que
tengan valores cuantizados del momento
angular:
ℎ
𝐿= 𝑛 = 𝑛ℏ
2𝜋
3. La energía de los electrones varía al cambiar de
nivel:
Δ𝐸 = ℎ𝜈
𝝂 se obtiene de la fórmula de Rydberg

29.  Halla la energía (eV) que debemos dar a un
electrón del nivel 2 para que salte hasta el
nivel 4.
 ℎ = 6′ 63 · 10−34 𝐽 · 𝑠
 𝑅 = 1′ 09677 · 107 𝑚−1
 𝑐 = 3 · 108 𝑚/𝑠
 1 𝑒𝑉 = 1′ 602 · 10−19 𝐽

30.  Calculamos primero la longitud de onda:
1 1 1
= 𝑅 2− 2
𝜆 𝑛1 𝑛2
1 ′ 7 −1
1 1
= 1 09677 · 10 𝑚 · − =
𝜆 4 16
𝜆 = 4′ 863 · 10−7 𝑚 ≈ 486 𝑛𝑚
Luz azul

31.  Calculamos ahora la energía de un fotón con
dicha longitud de onda:
𝑐
𝐸 = ℎ𝜈 = ℎ
𝜆
3 · 108 𝑚/𝑠
𝐸 = 6′ 63 · 10−34 𝐽· 𝑠· ′
4 863 · 10−7 𝑚
𝐸 = 4′ 09 · 10−19 𝐽 ≈ 2′ 55 𝑒𝑉

32. Dualidad onda – corpúsculo

33. Dualidad onda – corpúsculo
 De Broglie (Nobel en 1929):
 Dualidad onda – corpúsculo para todas las partículas.
Planck: 𝐸 = ℎ𝜈
ℎ𝜈 = 𝑚𝑐 2
Einstein: 𝐸 = 𝑚𝑐 2
𝑐 ℎ
𝜈= ⟶ 𝜆=
𝜆 𝑚· 𝑐

34. Dualidad onda – corpúsculo

35.  Halla la masa asociada a un fotón de luz roja,
con longitud de onda 7000 Å.
ℎ ℎ
𝜆= ⟶ 𝑚=
𝑚· 𝑐 𝜆· 𝑐
6′ 63 · 10−34 𝐽 · 𝑠
𝑚=
7 · 10−7 𝑚 · 3 · 108 𝑚/𝑠
𝑚 = 3′ 16 · 10−36 𝑘𝑔
Despreciable al lado de la longitud de onda.

36.  Calcula la longitud de onda asociada a una
persona de 70 𝑘𝑔 que se mueve a 1′ 4 𝑚/𝑠.
ℎ 6′ 63 · 10−34 𝐽 · 𝑠
𝜆= =
𝑚· 𝑣 70 𝑘𝑔 · 1′ 4 𝑚/𝑠
𝜆 = 6′ 77 · 10−36 𝑚
Despreciable frente a la masa de la persona.

37. Principio de incertidumbre

39. Principio de incertidumbre
 Heisenberg (Nobel 1932) determinó que no es
posible especificar para un 𝑒 − su posición y su
cantidad de movimiento simultáneamente.
 Una consecuencia inmediata es que ya no
podemos hablar de órbitas. Aparece el concepto
de orbital.

41. Principio de incertidumbre
 La imprecisión con que se pueden medir
ambas magnitudes es:
 También se aplica a la energía y al tiempo:

42.  Un 𝑒 − se mueve a 4000 𝑘𝑚/𝑠.
 La incertidumbre en su velocidad es del 3%.
 ¿Cuál es su incertidumbre en su posición?
 ℎ = 6′ 63 · 10−34 𝐽 · 𝑠
 𝑚 𝑒 = 9′ 11 · 10−31 𝑘𝑔

43.  De los datos del problema:
∆𝑣 = 0′ 03 · 4 · 105 𝑚/𝑠 = 1′ 2 · 105 𝑚/𝑠
 Aplicamos el Principio de Incertidumbre:
ℎ 6′ 63 · 10−34 𝐽 · 𝑠
∆𝑥 ≥ =
2𝜋 · ∆𝑝 2𝜋 · 9′ 11 · 10−31 𝑘𝑔 · 1′ 2 · 105 𝑚/𝑠
∆𝑥 ≥ 9′ 6 · 10−10 𝑚
Radio 𝑒 − ≈ 3 · 10−15 𝑚