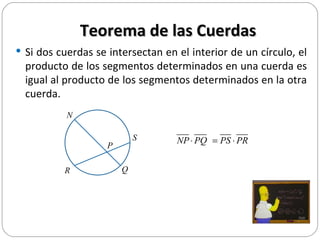
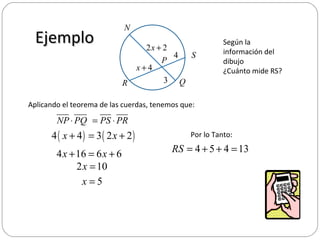
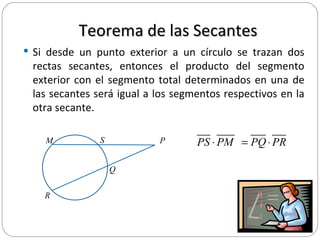
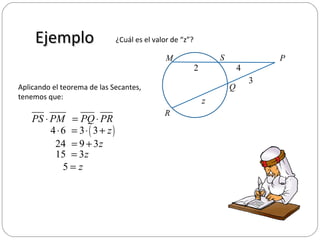
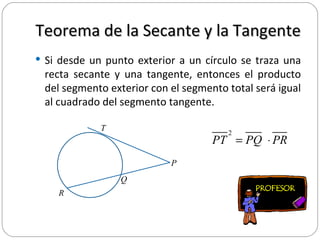
Este documento presenta tres teoremas relacionados con segmentos en una circunferencia: el teorema de las cuerdas, el teorema de las secantes y el teorema de la secante y la tangente. Explica cada teorema y proporciona un ejemplo numérico para ilustrar cómo aplicarlos para calcular longitudes desconocidas.

1. Profesor Practicante: Ignacio Espinoza Braz Segmentos en la Circunferencia Comunidad Educativa San Marcos Subsector de Matemática Arica

2. Hoy conoceremos: Teoremas relativos a segmentos en la circunferencia.

3. Teorema de las Cuerdas Si dos cuerdas se intersectan en el interior de un círculo, el producto de los segmentos determinados en una cuerda es igual al producto de los segmentos determinados en la otra cuerda.

4. Ejemplo Según la información del dibujo ¿Cuánto mide RS? Aplicando el teorema de las cuerdas, tenemos que: Por lo Tanto:

5. Teorema de las Secantes Si desde un punto exterior a un círculo se trazan dos rectas secantes, entonces el producto del segmento exterior con el segmento total determinados en una de las secantes será igual a los segmentos respectivos en la otra secante.

6. Ejemplo ¿Cuál es el valor de “z”? Aplicando el teorema de las Secantes, tenemos que:

7. Teorema de la Secante y la Tangente Si desde un punto exterior a un círculo se traza una recta secante y una tangente, entonces el producto del segmento exterior con el segmento total será igual al cuadrado del segmento tangente.

8. Ejemplo En la figura, el segmento PT, es un segmento tangente a la circunferencia que mide 6 cm. Si PQ mide 4 cm, entonces AB mide: Aplicando el teorema de la secante y la tangente, tenemos que: