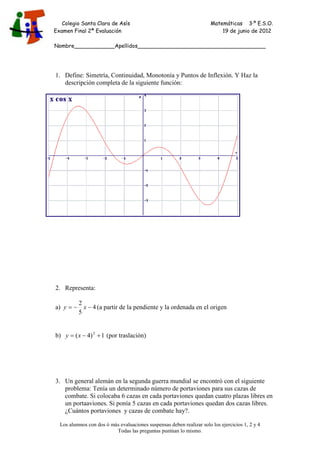
Este documento presenta un examen de matemáticas de 3er año de secundaria en España. Consiste en 6 preguntas que cubren temas como funciones, sistemas de ecuaciones, representación gráfica, y factorización de polinomios. Los estudiantes con dos o más evaluaciones suspendidas solo deben completar las preguntas 1, 2 y 4.

1. Colegio Santa Clara de Asís Matemáticas 3·º E.S.O.
Examen Final 2ª Evaluación 19 de junio de 2012
Nombre____________Apellidos______________________________________
Los alumnos con dos ó más evaluaciones suspensas deben realizar solo los ejercicios 1, 2 y 4
Todas las preguntas puntúan lo mismo.
1. Define: Simetría, Continuidad, Monotonía y Puntos de Inflexión. Y Haz la
descripción completa de la siguiente función:
2. Representa:
a) 4
5
2
 xy (a partir de la pendiente y la ordenada en el origen
b) 1)4( 2
 xy (por traslación)
3. Un general alemán en la segunda guerra mundial se encontró con el siguiente
problema: Tenía un determinado número de portaviones para sus cazas de
combate. Si colocaba 6 cazas en cada portaviones quedan cuatro plazas libres en
un portaaviones. Si ponía 5 cazas en cada portaviones quedan dos cazas libres.
¿Cuántos portaviones y cazas de combate hay?.

2. Colegio Santa Clara de Asís Matemáticas 3·º E.S.O.
Examen Final 2ª Evaluación 19 de junio de 2012
Nombre____________Apellidos______________________________________
Los alumnos con dos ó más evaluaciones suspensas deben realizar solo los ejercicios 1, 2 y 4
Todas las preguntas puntúan lo mismo.
4. Resuelve los siguientes sistemas y ecuaciones:
a)














0
2
2
3
21
0
3
1
2
1
yxy
yx
b) 0416 2
 xx
6. Factoriza el siguiente polinomio: P(x) = xx 1622 5
