Descargar para leer sin conexión
Más contenido relacionado
Camilo
- 1.
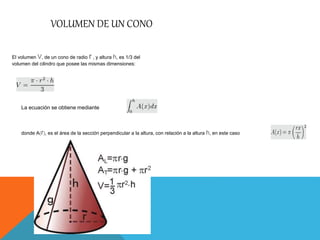
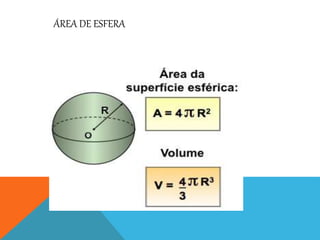
- 2. EL CONO En geometría,un cono recto es un sólido de revolución generado por el giro de un triángulo rectángulo alrededor de uno de sus catetos. Al círculo conformado por el otro cateto se denomina base y al punto donde confluyen las generatrices se llama vértice o cúspide.
- 3. VOLUMEN DE UNCONO El volumen V, de un cono de radio r , y altura h, es 1/3 del volumen del cilindro que posee las mismas dimensiones: La ecuación se obtiene mediante donde A(r), es el área de la sección perpendicular a la altura, con relación a la altura h, en este caso
- 4. ÁREA DE UNCONO
- 5. EJEMPLO DEL CONO Elvolumen de un cono se calcula haciendo: Vol. = 1/3 * área base * altura Al ser la base un círculo: Vol. = 1/3 * pi * r² * h Ejemplo: Encuentra el volumen de un cono que el radio de su base es 2,1cm y la altura 6cm, usando pi=22/7. Vol. = 1/3 * pi * r² * h Vol. = 1/3 * 22/7 * 2,1² * 6 Vol. = 27,72 cm³
- 6. EL CILINDRO En geometría,un cilindro es una superficie de las denominadas cuadrigas formada por el desplazamiento paralelo de una recta llamada generatriz a lo largo de una curva plana, que debe ser cerrada, denominada directriz del cilindro. Si la directriz es un círculo y la generatriz es perpendicular a él, entonces la superficie obtenida, llamada cilindro circular recto, será de revolución y tendrá por lo tanto todos sus puntos situados a una distancia fija de una línea recta, el eje del cilindro. El sólido encerrado por esta superficie y por dos planos perpendiculares al eje también es llamado cilindro. Este sólido es utilizado como una superficie Gaussiana.
- 7. VOLUMEN DE UNCILINDRO V = π R2 h V = Ab h donde V - cilindro volumen, Ab - área de las bases de la cilindro, R - radio de la cilindro, h - longitud de la altura de la cilindro, π = 3.141592.
- 8. ÁREA DE UNCILINDRO
- 9. EJEMPLO DE CILINDRO Elcilindro es un cuerpo geométrico que se caracteriza por su base circular. Por lo tanto, para el cálculo del volumen de un cilindro, es fundamental conocer la superficie de esa base y multiplicarla por la altura: Vol. = Superficie de la base * altura Vol. = pi * r² * h De este modo, si la altura del cilindro es de 25 cm y el radio de la base es de 3 cm, se verifica que: Vol = pi * r² * h Vol = 3.14 * (3 cm)² * 25 cm Vol = 3.14 * 9 cm² * 25 cm Vol = 706.5 cm³
- 10. LA ESFERA En geometría,una superficie esférica es una superficie de revolución formada por el conjunto de los puntos del espacio cuyos puntos equidistan de otro interior llamado centro. Los puntos cuya distancia es menor que la longitud del radio forman el interior de la superficie esférica. La unión del interior y la superficie esférica se llama bola cerrada.
- 11. VOLUMEN DE LAESFERA El volumen, V, de una esfera se expresa en función de su radio r, como: Se puede considerar el volumen de una esfera como 2/3 del volumen del cilindro circunscrito a la esfera. Su base es un círculo del mismo diámetro que la esfera. Su altura tiene la misma medida que dicho diámetro: Esta relación de volúmenes se adjudica a Arquímedes. Es posible calcular el volumen de una esfera con un margen de error aproximado al 0.03% sin utilizar el valor de π:
- 12.
- 13. EJEMPLO DE ESFERA Esposible demostrar que el volumen de una esfera es idéntico a las dos terceras partes del cilindro circunscrito en su interior. De forma simplificada, la fórmula para calcular el volumen de un esfera es: Vol. = 4/3 * pi * r³ Como ejemplo, si asumimos que la Tierra es esférica y que su radio en el Ecuador es de 6378 km, podemos calcular el volumen de nuestro planeta con la aplicación de esa fórmula: Vol = 4/3 * pi * r³ Vol = 4/3 * 3.14 * (6 378 km)³ Vol = 4/3 * 3.14 * 2.59 * 10¹¹ km³ Vol = 1.086 * 10¹² km³