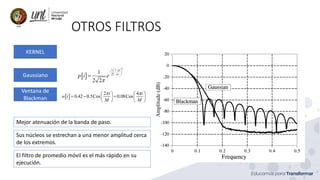
Este documento describe diferentes tipos de filtros digitales, incluyendo filtros de promedio móvil, filtros de ventana sinc y filtros personalizados. Explica que los filtros de promedio móvil son útiles para reducir ruido aleatorio y son fáciles de implementar mediante convolución. También describe cómo diseñar filtros de ventana sinc para separar bandas de frecuencia y cómo crear filtros personalizados.

2. PROCESAMIENTO DIGITAL DE
SEÑALES
SEÑALES Y SISTEMAS EN TIEMPO DISCRETO
Marcelo Fernando Valdiviezo Condolo
Quinto ‘A’
Carrera de Telecomunicaciones

3. FILTROS DIGITALES
JULIO - 2020

4. FILTROS DE PROMEDIO MÓVIL
Filtro mas común en
DSP
Óptimo para reducir
el ruido aleatorio
Fácil de entender y usar
Principal filtro para señales
en el dominio temporal
Gaussiano, Blackman
y Promedio Móvil de
Paso Múltiple

5. IMPLEMENTACIÓN POR
CONVOLUCIÓN
Funciona promediando un número de puntos de la señal de entrada para producir cada punto de la señal de
salida.
   
1
1
1 M
j
y i x i j
M
−
=
= + : Número de puntos a promediarM
 
         80 81 82 83 84
80
5
x x x x x
y
+ + + +
=
 
         78 79 80 81 82
80
5
x x x x x
y
+ + + +
=
Como alternativa, el grupo de puntos de la señal de entrada puede elegirse simétricamente alrededor del punto de salida
   
1
2
1
2
1
M
M
j
y i x i j
M
−
−
=−
= +
PROMEDIO
SIMÉTRICO
El filtro de promedio móvil es una convolución que utiliza un filtro con núcleo muy simple.

6. REDUCCIÓN DE RUIDO VS.
RESPUESTA AL ESCALÓN
Filtro de Promedio
Móvil

7. RESPUESTA EN FRECUENCIA
Respuesta en Frecuencia del Filtro de Promedio
Móvil
FFT
 
( )
( )
Sin
Sin
fM
H f
M f


= Respuesta en frecuencia de filtro de
promedio móvil de M puntos

8. FILTROS SEMEJANTES AL FILTRO DE
PROMEDIO VARIABLE
IDEAL REAL
Codificación
Dominio
Temporal
Codificación
Dominio
Frecuencial
Codificación
Dominio
Temporal -
Frecuencial
Señales de TV

9. FILTRO DE PROMEDIO VARIABLE DE
PASO MÚLTIPLE
Implican pasar la señal de entrada a través
de un filtro de promedio variable dos o
más veces.
En dos pasadas es el resultado de
convolucionar el pulso cuadrado consigo
mismo.
Cuatro o mas pasadas dan como resultado
algo parecido a un Gaussiano (Teorema del
Límite Central)
La respuesta al Escalón de múltiples pasos
se asemeja a una ‘S’
 
( )
( )
Sin
#
Sin
fM
H f Pasos
M f


= •
Respuesta en frecuencia

10. OTROS FILTROS
KERNEL
Gaussiano
Ventana de
Blackman  
2 4
0.42 0.5Cos 0.08Cos
i i
w i
M M
    
= − +   
   
 
2
1
21
2 2
i
p i e



− 
−  
 
=
Mejor atenuación de la banda de paso.
Sus núcleos se estrechan a una menor amplitud cerca
de los extremos.
El filtro de promedio móvil es el más rápido en su
ejecución.

11. APLICACIÓN RECURSIVA
 
             47 48 49 50 51 52 53
50
7
x x x x x x x
y
+ + + + + +
=
 
             48 49 50 51 52 53 54
51
7
x x x x x x x
y
+ + + + + +
=
 
     50 54 47
51
7
y x x
y
+ −
=
 
     1
7
y i x i p x i q
y i
− + + − −
=ECUACIÓN RECURSIVA
1
2
M
p
−
= 1q p= +

12. FILTROS DE ENVENTANADO-SINC
Se usan para separar
bandas de frecuencia
Pobre rendimiento en
el dominio del tiempo
Son muy estables con
increíbles niveles de
rendimiento.
Fáciles de programar
mediante convolución.
Se pude utilizar FFT
para mejorar la
velocidad.

13. ESTRATEGIA DE ENVENTANADO-SINC
 
( )Sin 2 cf i
h i
i


=
Se trunca a M + 1 puntos, elegidos simétricamente
alrededor del lóbulo principal, donde M es un
número par. Todas las muestras fuera de estos
puntos M + 1 se ponen a cero, o simplemente se
ignoran.
CASO IDEAL
Infinitos componentes positivos y negativos
diferentes de 0.
Efecto Gibbs

14. ESTRATEGIA DE ENVENTANADO-SINC
 
2 4
0.42 0.5Cos 0.08Cos
i i
w i
M M
    
= − +   
   
 
2
0.54 0.46Cos
i
w i
M
 
= −  
 

15. ESTRATEGIA DE ENVENTANADO-SINC
 
2 4
0.42 0.5Cos 0.08Cos
i i
w i
M M
    
= − +   
   
 
2
0.54 0.46Cos
i
w i
M
 
= −  
 
Ventana de Hamming
Ventana de Blackman

16. DISEÑANDO EL FILTRO SINC
Se deben seleccionar dos parámetros:
: Frecuencia de cortecf : Longitud del kernel del filtroM
4
cf
BW
=
BW es el ancho de la banda de transición, medido desde el punto en que la curva apenas sale de uno,
hasta el punto en que casi llega a cero (por ejemplo, del 99% al 1% de la curva).

17. DISEÑANDO EL FILTRO SINC
La forma de la respuesta en frecuencia
no depende de la frecuencia de corte
seleccionada.
La frecuencia de corte se mide en el
punto de media amplitud.
Simetría ideal para la inversión
espectral.

18. DISEÑANDO EL FILTRO SINC
Después de seleccionar la frecuencia de corte y M, el kernel del filtro se calcula a partir de:
 
Sin 2
2 2 4
0.42 0.5Cos 0.08Cos
2
c
M
f i
i i
h i K
M M Mi

 
  
−         = − +    
    −
Para que el filtro tenga ganancia unitaria en DC, la constante K debe ser elegida de tal manera que la suma de
todas las muestras sea igual a uno.

19. DISEÑOS DE FILTROS SINC
Las muestras al principio y fin del filtro aunque casi
imperceptibles son muy importantes
La representación de este tipo de filtro es punto
flotante para poder capturar la gran variación de
valores.

20. EJEMPLOS DE FILTROS SINC
Filtro de ondas alfa y beta de EEC
Filtro para aislar un tono de audio

21. FILTROS PERSONALIZADOS

22. FILTROS PERSONALIZADOS

23. DECONVOLUCIÓN

24. DECONVOLUCIÓN

25. PREGUNTAS

26. GRACIAS…