Descargar para leer sin conexión
Subido porJoe Arroyo Suárez
Clase21
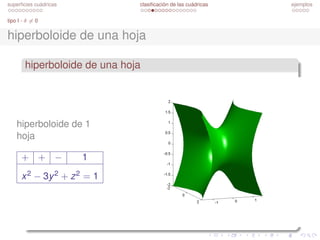
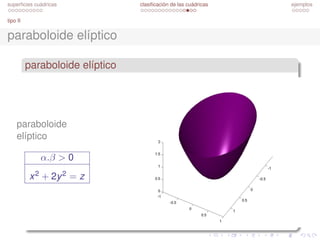
Este documento habla sobre las superficies cuádricas. Define una superficie cuádrica como una ecuación cuadrática en x, y y z. Explica que las superficies cuádricas se pueden clasificar en tipos I y II dependiendo de su forma reducida. Proporciona ejemplos de una esfera y el plano xy=0. Luego discute cómo llegar a la forma reducida de una cuádrica y clasificarla.
Más contenido relacionado
![La guerra del guano y el salitre todo[1]](https://cdn.slidesharecdn.com/ss_thumbnails/laguerradelguanoyelsalitretodo1-141205140249-conversion-gate02-thumbnail.jpg?width=640&height=640&fit=bounds)
Clase21
- 1. superficies cuádricas clasificaciónde las cuádricas ejemplos Superficies cuádricas Jana Rodriguez Hertz GAL2 IMERL 9 de noviembre de 2010
- 2. superficies cuádricas clasificaciónde las cuádricas ejemplos definición superficie cuádrica definición (forma cuadrática) una superficie cuádrica está dada por la ecuación:
- 3. superficies cuádricas clasificaciónde las cuádricas ejemplos definición superficie cuádrica definición (forma cuadrática) una superficie cuádrica está dada por la ecuación: a11x2+a22y2+a33z2+2a12xy+2a13xz+2a23yz+2b1x+2b2y+2b3z+c=0
- 4. superficies cuádricas clasificaciónde las cuádricas ejemplos definición superficie cuádrica definición (forma cuadrática) una superficie cuádrica está dada por la ecuación: a11x2+a22y2+a33z2+2a12xy+2a13xz+2a23yz+2b1x+2b2y+2b3z+c=0 o, equivalentemente, XtAX + 2BtX + c = 0
- 5. superficies cuádricas clasificaciónde las cuádricas ejemplos definición superficie cuádrica definición (forma cuadrática) una superficie cuádrica está dada por la ecuación: a11x2+a22y2+a33z2+2a12xy+2a13xz+2a23yz+2b1x+2b2y+2b3z+c=0 o, equivalentemente, XtAX + 2BtX + c = 0 con A matriz simétrica, B vector de R3, c constante.
- 6. superficies cuádricas clasificaciónde las cuádricas ejemplos definición ejemplo 1 ejemplo 1 la esfera unitaria x2 + y2 + z2 = 1 es una cuádrica
- 7. superficies cuádricas clasificaciónde las cuádricas ejemplos definición ejemplo 1 ejemplo 1 la esfera unitaria x2 + y2 + z2 = 1 es una cuádrica
- 8. superficies cuádricas clasificaciónde las cuádricas ejemplos definición ejemplo 2 ejemplo 2 la cuádrica xy = 0
- 9. superficies cuádricas clasificaciónde las cuádricas ejemplos definición ejemplo 2 ejemplo 2 la cuádrica xy = 0 es la unión del plano x = 0 con el plano y = 0
- 10. superficies cuádricas clasificaciónde las cuádricas ejemplos definición ejemplo 2 ejemplo 2 la cuádrica xy = 0 es la unión del plano x = 0 con el plano y = 0
- 11. superficies cuádricas clasificaciónde las cuádricas ejemplos forma reducida ecuación reducida Nuestro objetivo es hacer un cambio de variables para que la cuádrica quede en una forma reducida:
- 12. superficies cuádricas clasificaciónde las cuádricas ejemplos forma reducida ecuación reducida Nuestro objetivo es hacer un cambio de variables para que la cuádrica quede en una forma reducida: definición ecuación reducida de una cuádrica:
- 13. superficies cuádricas clasificaciónde las cuádricas ejemplos forma reducida ecuación reducida Nuestro objetivo es hacer un cambio de variables para que la cuádrica quede en una forma reducida: definición ecuación reducida de una cuádrica: se obtiene por un cambio de variables ortogonal
- 14. superficies cuádricas clasificaciónde las cuádricas ejemplos forma reducida ecuación reducida Nuestro objetivo es hacer un cambio de variables para que la cuádrica quede en una forma reducida: definición ecuación reducida de una cuádrica: se obtiene por un cambio de variables ortogonal y tiene uno de los siguientes tipos:
- 15. superficies cuádricas clasificaciónde las cuádricas ejemplos forma reducida ecuación reducida Nuestro objetivo es hacer un cambio de variables para que la cuádrica quede en una forma reducida: definición ecuación reducida de una cuádrica: se obtiene por un cambio de variables ortogonal y tiene uno de los siguientes tipos: 1 tipo I: x2 +
- 16. y2 + z2+ = 0
- 17. superficies cuádricas clasificaciónde las cuádricas ejemplos forma reducida ecuación reducida Nuestro objetivo es hacer un cambio de variables para que la cuádrica quede en una forma reducida: definición ecuación reducida de una cuádrica: se obtiene por un cambio de variables ortogonal y tiene uno de los siguientes tipos: 1 tipo I: x2 +
- 18. y2 + z2+ = 0 2 tipo II: x2 +
- 19. y2 + z= 0
- 20. superficies cuádricas clasificaciónde las cuádricas ejemplos forma reducida ejemplos ejemplo el ejemplo 1 (esfera) es de tipo I con =
- 21. = =1 y = 1
- 22. superficies cuádricas clasificaciónde las cuádricas ejemplos forma reducida ejemplos ejemplo el ejemplo 1 (esfera) es de tipo I con =
- 23. = =1 y = 1 el ejemplo 2 (xy = 0) no está en su forma reducida, ya veremos cuál es
- 24. superficies cuádricas clasificaciónde las cuádricas ejemplos forma reducida objetivos 1 ver cómo se llega a una ecuación reducida
- 25. superficies cuádricas clasificaciónde las cuádricas ejemplos forma reducida objetivos 1 ver cómo se llega a una ecuación reducida 2 ver cuál es el dibujo de la superficie en su forma reducida
- 26. superficies cuádricas clasificaciónde las cuádricas ejemplos centro de una cuádrica centro de una cuádrica definición XtAX + 2BtX + c = 0 cuádrica
- 27. superficies cuádricas clasificaciónde las cuádricas ejemplos centro de una cuádrica centro de una cuádrica definición XtAX + 2BtX + c = 0 cuádrica Q = (xQ; yQ; zQ) centro de la cuádrica si
- 28. superficies cuádricas clasificaciónde las cuádricas ejemplos centro de una cuádrica centro de una cuádrica definición XtAX + 2BtX + c = 0 cuádrica Q = (xQ; yQ; zQ) centro de la cuádrica si A 0 @ xQ yQ zQ 1 A + B = ~0
- 29. superficies cuádricas clasificaciónde las cuádricas ejemplos centro de una cuádrica observación puede haber un único centro (sistema compatible determinado)
- 30. superficies cuádricas clasificaciónde las cuádricas ejemplos centro de una cuádrica observación puede haber un único centro (sistema compatible determinado) puede haber infinitos centros (sistema compatible indeterminado)
- 31. superficies cuádricas clasificaciónde las cuádricas ejemplos centro de una cuádrica observación puede haber un único centro (sistema compatible determinado) puede haber infinitos centros (sistema compatible indeterminado) puede no haber centros (sistema incompatible)
- 32. superficies cuádricas clasificaciónde las cuádricas ejemplos teoremas centro y clasificación de cuádricas teorema 1 F(x; y; z) = XtAX + 2BtX + c = 0 cuádrica
- 33. superficies cuádricas clasificaciónde las cuádricas ejemplos teoremas centro y clasificación de cuádricas teorema 1 F(x; y; z) = XtAX + 2BtX + c = 0 cuádrica P1AP = diag(;
- 34. ; ) conP ortogonal
- 35. superficies cuádricas clasificaciónde las cuádricas ejemplos teoremas centro y clasificación de cuádricas teorema 1 F(x; y; z) = XtAX + 2BtX + c = 0 cuádrica P1AP = diag(;
- 36. ; ) conP ortogonal Si existe un centro Q = (xQ; yQ; zQ)t , entonces
- 37. superficies cuádricas clasificaciónde las cuádricas ejemplos teoremas centro y clasificación de cuádricas teorema 1 F(x; y; z) = XtAX + 2BtX + c = 0 cuádrica P1AP = diag(;
- 38. ; ) conP ortogonal Si existe un centro Q = (xQ; yQ; zQ)t , entonces haciendo el cambio de variables X = PX0 + Q
- 39. superficies cuádricas clasificaciónde las cuádricas ejemplos teoremas centro y clasificación de cuádricas teorema 1 F(x; y; z) = XtAX + 2BtX + c = 0 cuádrica P1AP = diag(;
- 40. ; ) conP ortogonal Si existe un centro Q = (xQ; yQ; zQ)t , entonces haciendo el cambio de variables X = PX0 + Q la cuádrica queda tipo I: x02 +
- 41. y02 + z02+ F(Q) = 0
- 42. superficies cuádricas clasificaciónde las cuádricas ejemplos teoremas cuando no hay centro teorema 2 Si la cuádrica XtAX + 2BtX + c = 0 no tiene centro
- 43. superficies cuádricas clasificaciónde las cuádricas ejemplos teoremas cuando no hay centro teorema 2 Si la cuádrica XtAX + 2BtX + c = 0 no tiene centro ) PtAP = diag(;
- 44.
- 45. superficies cuádricas clasificaciónde las cuádricas ejemplos teoremas cuando no hay centro teorema 2 Si la cuádrica XtAX + 2BtX + c = 0 no tiene centro ) PtAP = diag(;
- 46. ; 0) y la ecuación reducida es de tipo II: x02 +
- 47. y0z + z0= 0 con 6= 0
- 48. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I cuádricas de tipo I tipo I x2 +
- 49. y2 + z2+ = 0 cuádrica de tipo I
- 50. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I cuádricas de tipo I tipo I x2 +
- 51. y2 + z2+ = 0 cuádrica de tipo I hay dos casos importantes:
- 52. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I cuádricas de tipo I tipo I x2 +
- 53. y2 + z2+ = 0 cuádrica de tipo I hay dos casos importantes: 1 6= 0
- 54. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I cuádricas de tipo I tipo I x2 +
- 55. y2 + z2+ = 0 cuádrica de tipo I hay dos casos importantes: 1 6= 0 2 = 0
- 56. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I cuádricas de tipo I tipo I x2 +
- 57. y2 + z2+ = 0 cuádrica de tipo I hay dos casos importantes: 1 6= 0 ! 0x2 +
- 58. 0y2 + 0z2= 1 2 = 0
- 59. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I cuádricas de tipo I tipo I x2 +
- 60. y2 + z2+ = 0 cuádrica de tipo I hay dos casos importantes: 1 6= 0 ! 0x2 +
- 61. 0y2 + 0z2= 1 2 = 0 ! x2 +
- 62. y2 + z2= 0
- 63. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I clasificación de cuádricas de tipo I clasificación cómo se clasifican?
- 64. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I clasificación de cuádricas de tipo I clasificación cómo se clasifican? 1ero por 6= 0 o 6= 0
- 65. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I clasificación de cuádricas de tipo I clasificación cómo se clasifican? 1ero por 6= 0 o 6= 0 luego por signo de ;
- 66.
- 67. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I - 6= 0 elipsoide elipsoide elipsoide + + + 1 3x2 + y2 + 4z2 = 1
- 68. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I - 6= 0 elipsoide elipsoide elipsoide + + + 1 3x2 + y2 + 4z2 = 1
- 69. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I - 6= 0 hiperboloide de una hoja hiperboloide de una hoja hiperboloide de 1 hoja + + 1 x2 3y2 + z2 = 1
- 70. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I - 6= 0 hiperboloide de una hoja hiperboloide de una hoja hiperboloide de 1 hoja + + 1 x2 3y2 + z2 = 1
- 71. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I - 6= 0 hiperboloide de dos hojas hiperboloide de dos hojas hiperboloide de 2 hojas + 1 x2 + y2 z2 = 1
- 72. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I - 6= 0 hiperboloide de dos hojas hiperboloide de dos hojas hiperboloide de 2 hojas + 1 x2 + y2 z2 = 1
- 73. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I - 6= 0 cilindro elíptico cilindro elíptico cilindro elíptico + + 0 1 x2 + 2y2 = 1
- 74. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I - 6= 0 cilindro elíptico cilindro elíptico cilindro elíptico + + 0 1 x2 + 2y2 = 1
- 75. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I - 6= 0 cilindro hiperbólico cilindro hiperbólico cilindro elíptico + 0 1 x2 y2 = 1
- 76. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I - 6= 0 cilindro hiperbólico cilindro hiperbólico cilindro elíptico + 0 1 x2 y2 = 1
- 77. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I - 6= 0 dos planos paralelos dos planos paralelos dos planos paralelos + 0 0 1 4x2 = 1
- 78. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I - 6= 0 dos planos paralelos dos planos paralelos dos planos paralelos + 0 0 1 4x2 = 1
- 79. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I - 6= 0 otros casos 1 ! ; 0 1 ! ; 0 0 1 ! ;
- 80. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I - = 0 cono cono cono + + 0 + 0 x2 + 2y2 z2 = 0
- 81. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I - = 0 cono cono cono + + 0 + 0 x2 + 2y2 z2 = 0
- 82. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I - = 0 planos que se cortan planos que se cortan planos que se cortan + + 0 + 0 x2 y2 = 0
- 83. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I - = 0 planos que se cortan planos que se cortan planos que se cortan + + 0 + 0 x2 y2 = 0
- 84. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo I - = 0 otros casos 0 un punto 0 0 una recta 0 0 0 un plano
- 85. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo II tipo II tipo II x2 +
- 86. y2 + z= 0 con 6= 0
- 87. superficies cuádricas clasificaciónde las cuádricas ejemplos tipo II tipo II tipo II x2 +
- 88. y2 + z= 0 con 6= 0 cómo se clasifican: