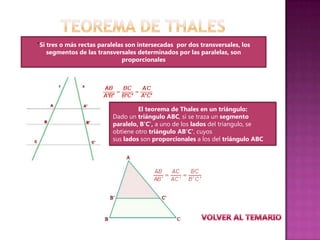
El documento resume conceptos matemáticos fundamentales como números reales, potenciación, porcentajes, notación científica, expresiones algebraicas, ecuaciones, funciones y proporcionalidad. Explica cada uno de estos temas de manera concisa definiendo sus características principales y proporcionando ejemplos ilustrativos.

2.  Números Reales
 Potenciación - Radicación
 Porcentaje
 Notación Científica
 Expresiones Algebraicas
 Ecuaciones e Inecuaciones
 Funciones
 Proporcionalidad Directa – Inversa
 Sistema de Ecuación Lineal
 Teorema de Thales
 Unidades de Longitud-Superficie-Volumen-
Capacidad

3. Se denomina así, a todo número que Un numero es irracional cuando no puede
puede representarse como ser expresado como cociente entre dos
el cociente de dos números enteros ,es números enteros, y su expresión decimal
decir, una fracción común a/b con tiene una cantidad de cifras decimales no
numerador a y denominador b distinto periódicas.
de cero. El conjunto de los números Ejemplo:
racionales se denota por Q, que deriva
=3.141592653589
de «cociente». Este conjunto de
números incluye a los números
enteros , y es un subconjunto de
los números reales.
Ejemplo:

4. Potencia de exponente 0: Un número distinto de 0 elevado al exponente 0 da como resultado la unidad , puesto
que:
Potencia de exponente 1: Toda potencia de exponente 1 es igual a la base:
Potencia de exponente negativo: Un número elevado a un exponente negativo, es igual al inverso de la misma
expresión pero con exponente positivo:
Multiplicación de potencias de igual base: El producto de dos potencias que tienen la misma base es igual a una
potencia de dicha base que tiene como exponente la suma de los exponentes, es decir:
División de potencias de igual base: El cociente de dos potencias que tienen la misma base es igual a una
potencia de dicha base que tiene como exponente el resultado de restar el exponente del divisor al del dividendo,
es decir:
Potencia de un producto: La potencia de un producto es igual al producto de cada uno de los factores elevado al
mismo exponente, es decir:
Potencia de una potencia: La potencia de una potencia de base a es igual a la potencia de base a y cuyo
exponente es el producto de ambos exponentes (la misma base y se multiplican los exponentes):
Debido a esto, la notación se reserva para significar ya que se puede escribir sencillamente como:
Potencia de un cociente: La potencia de un cociente es igual al cociente de cada uno de los números elevado al
mismo exponente.
Potencia de base 10: Desplazar la coma decimal tantas posiciones como indique el exponente, hacia la izquierda si
el exponente es negativo, o hacia la derecha si el exponente es positivo.

5.  Raíz de un producto: La raíz de un producto de factores es igual al
producto de las raíces de los factores. Con n distinto de cero (0).
Ejemplo:
 Raíz de un cociente: La raíz de una fracción es igual al cociente de la
raíz del numerador entre la raíz del denominador.
Cuando esta propiedad se hace con números no hace falta pasar la
raíz a potencia de exponente racional, aunque sí cuando se hace con
variables.
=
n distinto de cero (0).
 Raíz de una raíz: Para calcular la raíz de una raíz se multiplican los
índices de las raíces y se conserva el radicando.
=
n y m distintos de cero (0).

6. Un porcentaje es una forma de expresar un número como una fracción de 100 (por ciento, que
significa “de cada 100”).
El A% de B, es tomar A de las 100 partes en que se divide B: A . B/100 = B . A/100
Ej: el 15% de 180 es: 180. 15/100 = 180.0,15
Para determinar el porcentaje de un número sigue los siguientes pasos:
1. Multiplica el número por el porcentaje (ej. 87 * 68 = 5916)
2. Divide el resultado por 100 (Mueve el punto decimal dos lugares hacia la izquierda) (ej.
5916/100=59.16)
3. Redondea a la precisión deseada (ej. 59.16 redondeado al número entero más próximo=59)

7. La notación científica se utiliza en ciencias. Permite escribir de manera simplificada
números largos y cortos.
La notación científica debe estar escrito como el producto entre un numero mayor o igual
que 1 y menor que diez y una potencia de 10 con un exponente que equivale a la
cantidad de números existentes después del primer número entero.
Si el numero es decimal, el exponente será negativo y se contarán, la cantidad de ceros
hacia la izquierda que indicará el exponente, a partir del primer numero entero.
*Para realizar operaciones se utilizan las propiedades de la potenciación (producto de
potencia de igual base, cociente de potencia de igual base)
 Por ejemplo: Un número como:
156.234.000.000.000.000.000.000.000.000 puede ser escrito como
1,56234*1029
 Potencias de 10: 10=101 100=102 100=103 0,01=10-1 0,001=10-2
Por ejemplo: 3,5*105=350000
9,6*10-4=0,00096

8.  Una expresión algebraica es una expresión en la que se relacionan valores
indeterminados con constantes y cifras, todas ellas ligadas por un número finito de
operaciones de suma, resta, producto, cociente, potencia y raíz.
 Ejemplos
2
a) x 2 xy
2 3
b) 2x y x
x. y 2x
c) 2
x 1
Expresiones Algebraicas
Racionales Irracionales
Enteras Fraccionarias
Polinomios Racionales

9. Las expresiones algebraicas enteras son polinomios.
Cuando en algún polinomio haya términos semejantes (x elevada al mismo exponente) se
deben sumar o restar para obtener un polinomio reducido, con el cual se debe
trabajar siempre.
Ej: P(x) = 3x3 – 6x + 2x + 10x +3 – 7x = 3x3 – x
Los números que multiplican a la variable son los coeficientes
El grado (GR) es el mayor exponente de todas las variables (3)
El coeficiente principal (CP) es el mayor numero que multiplica a una variable(10)
El termino independiente es el q no esta multiplicado por ninguna variable (8)
Binomio Trinomio Cuatrinomio Polinomio de x
términos
2 términos 3 términos 4 términos Ej de 5 terminos
Ej: 1/4x2- 8 Ej:1/4x2- 8 + 1/4x2- 8+3x +
3x 5x3

10.  Una ecuación es una igualdad entre dos expresiones algebraicas, denominadas miembros, en las
que aparecen valores conocidos o datos, y desconocidos o incógnitas, relacionados mediante
operaciones matemáticas. Los valores conocidos pueden ser números, coeficientes o constantes; y
también variables cuya magnitud se haya establecido como resultado de otras operaciones. Las
incógnitas, representadas generalmente por letras, constituyen los valores que se pretende hallar. Por
ejemplo, en la ecuación:
 Las soluciones son los valores que deben tomar las letras para que la igualdad sea cierta.
2x − 3 = 3x + 2 Rta: x = −5 Verificación: -5*2-3=-5*3+2
-10-3=-15+2
-13=-13
Las ecuaciones se clasifican en enteras, fraccionarias e irracionales.
 Una ecuación es entera cuando las incógnitas están sometidas únicamente a las operaciones de suma,
resta y multiplicación:
x + 1/5 = 2x - √5
 Una ecuación es fraccionaria cuando por lo menos una de las incógnitas figura en el divisor:
y +1 = y+2
x-1 x x
 Una ecuación es irracional cuando por lo menos una incógnita figura bajo el signo del radical:
3√x +1 =3

11. Una inecuación es una expresión matemática la cual se caracteriza por tener los signos
de orden (<, >, ≤ o ≥). Siendo una expresión algebraica nos da como resultado
un conjunto en el cual la variable independiente puede tomar el valor cualquiera de
ese conjunto cumpliendo esta desigualdad. A este conjunto se le conoce
como intervalo. Una de las obligaciones de las (inecuaciones) es la de cumplir una
desigualdad.
 Características generales de las inecuaciones
Sea por ejemplo: 5x + 15 > 30
Miembros de una inecuación son las partes separadas por el signo de la desigual. La
parte que está a la izquierda se llama primer miembro (5x + 15) y el segundo
miembro (30). Términos de una inecuación son cada una de las
expresiones literales (5x) o numéricas (15 y 30)separadas por el signo + o el signo .
Resolver una inecuación es hallar el conjunto solución. En la inecuación dada el conjunto
solución es { x > 3 }. El grado de una inecuación está indicado por el mayor exponente
de la variable. En el ejemplo el exponente de la variable es 1.
Procedimiento para resolución de una inecuación
1)Suprimimos signos de colección.
2)Hacemos transposición de términos escribiendo los que son independientes en uno de
los miembros y los que no lo son en el otro miembro de la inecuación.
3)Efectuamos reducción de términos semejantes en cada miembro.
4)Despejamos la incógnita.
Ejemplo:
5x + 15 > 30
5x > 30 – 15
5x> 15
x > 15/5
x>3
Verificación:
4*5 + 15 > 30

12. Una función es la relación entre estas dos variables:
• Variable independiente: letra "X"
• Variable dependiente: letra "Y", depende de X
En una función a cada valor de la variable independiente le corresponde un único valor de la variable
dependiente
Las funciones se pueden expresar mediante un gráfico, una tabla de valores o una formula
Formula: Y=3.X X ES LA VARIABLE INDEPENDIENTE.
EL RESULTADO DE Y DEPENDE DE X

13. Y = MX
 Su gráfica es una línea recta que pasa por el origen de coordenadas.
y = 2x X 0 1 2 3 4 5
Y 0 2 4 6 8 10
M es la pendiente: m es la pendiente de la recta. La pendiente es la inclinación de la recta con respecto al eje
de abscisas.
 Si m > 0 la función es creciente y el ángulo que forma la recta con la parte positiva del eje OX es agudo.
 Si m < 0 la función es decreciente y el ángulo que forma la recta con la parte positiva del eje OX es obtuso.

14.  Directa:
 Dos variables x e y son directamente proporcionales si su razón y/x es constante. En este caso se dice que
las variables x e y son directamente proporcionales.
 Dicho de otra manera si una de las variables aumenta (x), la otra también aumenta (y); y si una de las
variables disminuye (x), la otra también disminuye (y).
Una lata de bebida cuesta 350 pesos. Tienes que comprar 10;
por lo tanto, necesitas 3500 pesos.
Cantidad de latas (X) Costo en dinero
Con estos datos tenemos siguiente tabla:
(Y)
Como se aprecia, tenemos dos variables la cantidad de latas y
el costo en dinero, en ambas los valores aumentan
1 350 y a cada valor le corresponde un valor y sólo uno en la otra.
2 700
3 1050
4 1400
5 1750
6 2100
7 2450
8 2800
9 3150
10 3500

15.  Indirecta:
 Dos variables x e y son inversamente proporcionales si su producto x por y es constante. En este
caso se dice que las variables x e y son inversamente proporcionales.
 Dicho de otra manera si una de las variables aumenta (x), la otra disminuye (y); y si una de las
variables disminuye (x), la otra variable aumenta (y).
Estás invitado a un cumpleaños y como es habitual, hay una torta para compartir con el festejado. A
la fiesta asisten 10 amigos. A la hora de repartir la torta (si se hace en partes iguales) le corresponde
una (1) parte de diez a cada uno, es decir, una décima parte de la torta o también el 10 % del total.
Invitados (personas) Trozos de torta Con estos datos tenemos siguiente tabla:
(%) Como se aprecia, tenemos dos variables invitados ( personas) y Trozos
de torta (%), en una los valores aumentan y en la otra los valores
1 100,00
disminuyen.
2 50,00 y a cada valor le corresponde un valor y sólo uno en la otra.
3 33,33
4 25,00
5 20,00
6 16,66
7 14,28
8 12,50
9 11,11
10 10,00
11 9,09
12 8,33

16. En las matemáticas, un sistema de ecuaciones es un conjunto de dos o más ecuaciones. con varias incógnitas
que conforman un problema matemático consistente en encontrar las incógnitas que satisfacen dichas
ecuaciones.
Un sistema lineal con dos ecuaciones y dos incógnitas está formado por dos ecuaciones lineales y dos
indeterminadas, generalmente x e y. Resolverlo consiste en determinar los valores de x e y que hacen ciertas
simultáneamente las dos igualdades.
Un sistema de este tipo puede no tener solución (sistema incompatible), tener una solución (sistema
compatible determinado) o tener infinitas soluciones (sistema compatible indeterminado)
TIPOS:
 Sistema incompatible cuando no admite ninguna solución.
 Sistema compatible cuando admite alguna solución que a su vez pueden dividirse en:
 Sistemas compatibles indeterminados cuando existe un número infinito de soluciones que forman
una variedad continua.
 Sistemas compatibles determinados cuando admiten un conjunto finito de soluciones, o un
conjunto infinito de soluciones aisladas con a lo sumo un número finito de puntos de acumulación.
Ejemplo de un sistema de ecuación : 3 x - y = 5 / x+y=7
Analíticamente podemos resolverlo por varios métodos. Probamos con el método de igualación donde
despejaremos la variable y:
y=3x-5 e y=-x+7
Igualando ambas ecuaciones:
3 x - 5 = -x + 7
3x+x=7+5
4 x = 12
x=3
Entonces si x = 3 ; y = 4 Es decir que la solución del sistema es (3 , 4 )

17. "Si tres o más rectas paralelas son intersecadas por dos transversales, los
segmentos de las transversales determinados por las paralelas, son
proporcionales
El teorema de Thales en un triángulo:
Dado un triángulo ABC, si se traza un segmento
paralelo, B'C', a uno de los lados del triangulo, se
obtiene otro triángulo AB'C', cuyos
sus lados son proporcionales a los del triángulo ABC

18. La unidad de longitud: metro (M)
 Sus submúltiplos se obtienen dividiéndola por 10
 Mientras que sus múltiplos se obtienen multiplicándola por 10
Km hm dam m dm cm mm
0,001 0,01 0,1 1 10 100 1000
La unidad de capacidad: litro (l)
 Sus submúltiplos se obtienen dividiéndola por 10
 Mientras que sus múltiplos se obtienen multiplicándola por 10
Kl hl dla l dl cl ml
0,001 0,01 0,1 1 10 100 1000
La unidad de peso: gramo (g)
 Sus submiltiplos se obtienen dividiéndola por 10
 Mientras que sus múltiplos se obtienen multiplicándola por 10
kg hg dag g dg cg mg
0,001 0,01 0,1 1 10 100 1000
 La unidad de volumen: metro cúbico (m3)
 Sus submúltiplos se obtienen dividiéndola por 100
 Mientras que sus múltiplos se obtienen multiplicándola por 100
km3 hm3 dam3 m3 dm3 cm3 mm3
0,000000001 0,000001 0,001 1 100 100.000 1.000.000.000

19. Trabajo realizado por:
 José Cancinos
 Leandro Altobelli
 Francisco Villagra Segura.
Alumnos de 3° 1° de Economía
Profesora Juliana Isola
Año: 2012

20.  Libro de 9no año. “Matemáticas 3/9” Ed.
Kapelusz
 Internet:
 www.wikipedia.com
 www.vitutor.com