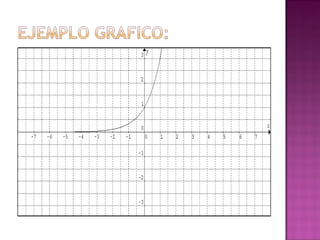
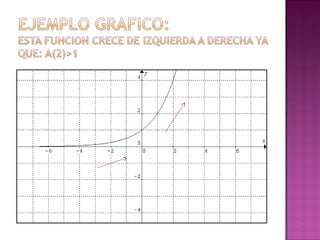
Este documento describe la función exponencial, cuyo dominio son los números reales y cuya imagen son los números reales positivos. Explica que la función crece cuando el exponente es mayor que 1 y decrece cuando es entre 0 y 1. También indica que la función exponencial es biyectiva porque no hay dos valores de x que tengan la misma imagen ni elementos de y que no sean imagen de algún x.

1. Por: Nadim Romano, Agustina Martinez,
Luciana Mirabella, Simón Jerez

2.  Se llama función exponencial a aquella
cuya forma genérica es F(x)= a^x siendo
“a” un numero mayor a 1. También se
considera como función exponencial a la
expresión y= a^x

3.  El dominio de esta función son todos los
elementos de la variable independiente x,
perteneciente al campo de los números
reales.
 La imagen son todos los valores
pertenecientes a Y, que solo
corresponden a los números reales
positivos

4.  F(X)= a^x
 Y= 3ⁿ
 DOMINIO:
 {1;2;0;-1;-2}
 IMAGEN:
 {3;9;1;0;3;0;1}
X Y
1 3^1=3
2 3^2=9
0 3^0=1
-1 3^-1=0,3
-2 3^-2=0,1

6.  El crecimiento de
la función crece
cuando a>1
 Por ejemplo:
 F(X)= a^x
 Y= 2^x
X Y
2 2^2=4
1 2^1=2
0 2^0=1
-1 2^-1=0.5
-2 2^-2=0,25

8.  El decrecimiento
de la función se
produce cuando:
 0<a<1
 Por ejemplo:
 Y=1/2^X
X Y
1 1/2^1
2 1/2^2
0 1/2^0
-1 1/2^-1
-2 1/2^-2

10.  Es una recta tal que la distancia de un
punto de una curva a esta recta tiene a 0
cuando el punto se aleja hacia el infinito
sobre la curva.

11. Inyectivas Sobneyectivas Biyectiva
CUANDO NO HAY DOS
VALORES DE x
DISTINTOS QUE
TENGAN LA MISMA
IMAGEN Y
CUANDO NO HAY
NINGUN ELEMENTO
DE Y QUE NO SEA
IMAGEN DE NINGUNO
DE X
CUANDO SON
INYECTIVAS Y
BIYECTIVAS A LA VEZ

12.  La función exponencial es biyectiva porque
no hay dos valores distintos para x que
tengan la misma imagen (y) y no hay ningún
elemento de y que no sea imagen de alguno
de x.
Otras formas de la funcion exponencial:

13. F(X)= K x a ^ x-b + c
 Funciones de la forma f(x) = K x a ^ x: K
modifica el valor de la ordenada
 Funciones de la forma f(X) = k x a ^ x-b : B
indica en corrimiento sobre el eje X
B CORRIMIENTO
0 NO TIENE
-1 1 HACIA LA IZQUIERDA
1 1 HACIA LA DERECHA

14.  Funciones de la forma f(x) = a ^ x + c : C
indica el corrimiento sobre el eje Y
C CORRIMIENTO
0 NO TIENE
1 Hacia arriba, 1.
-1 Hacia abajo, 1.

15.  Para graficar tener en cuenta las funciones
de K, B Y C. Además de las intersecciones
con el eje X (y=0) y con el eje y (x=0)
 El punto C es el que determina la asíntota
horizontal