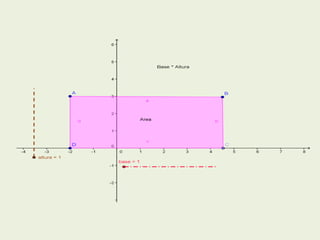
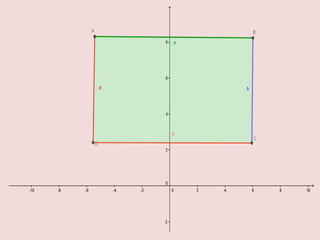
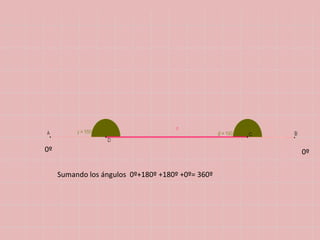
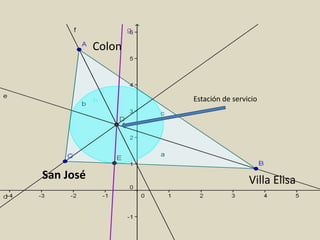
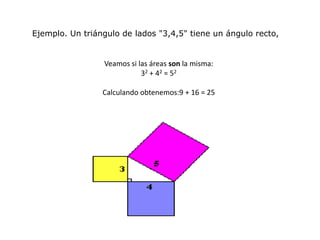
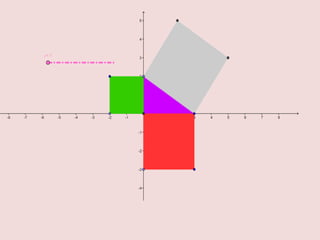
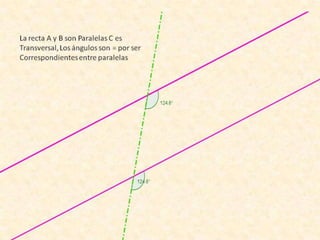
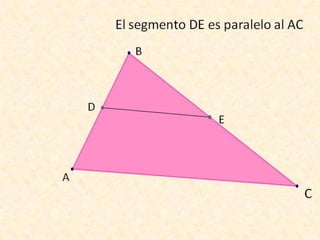
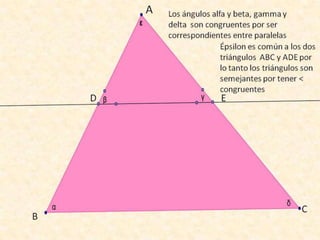
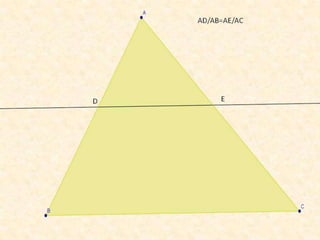
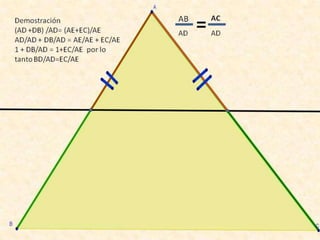
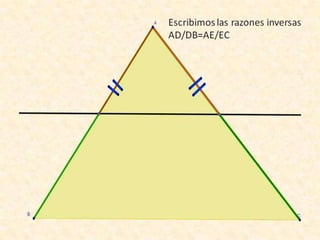
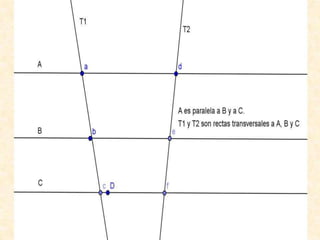
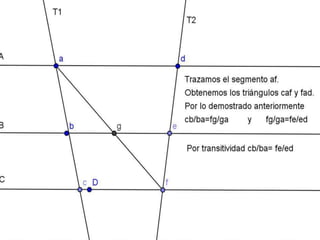
Este documento resume varios conceptos y demostraciones de geometría presentados en un taller, incluyendo el área del rectángulo, la suma de los ángulos interiores de un cuadrilatero que es igual a 360°, la demostración del teorema de Pitágoras, y aplicaciones prácticas de bisectrices e incentro para encontrar el centro de un triángulo.

1. Resumen de actividades Taller de GeometríaOctubre 2011Cursante : Silveyra AdrianaÁrea del Rectángulo

2. Este Appet esta pensado para hallar el área del rectángulo cuando su altura y base son medidas variables que oscilan entre 1 y 25 respectivamente

4. Suma de los ángulos interiores deUn cuadrilatero

5. Suma de los ángulos interiores de un cuadrilatero

6. Demostración : los ángulos interiores de un rectángulo es igual a 360ºSe traza un rectángulo y se marcan sus ángulosLos lados laterales se pintan de rojo y azul.Al moverlos desarmando el rectángulo de modo que queden todos los lados alineados en línea recta se vera que los ángulos que quedan son, dos de 180º y dos de 0ºSi se Mueve los puntos azules de manera que los lados queden en línea recta, se formaran dos ángulos llanos que sumados dan 360º

8. 0º0ºSumando los ángulos 0º+180º +180º +0º= 360º

9. Bisectrices -Incentro

10. Aplicación Practica de bisectrices-Incentro Partiendo de este problema : por ejemplo que hay 3 ciudades (vértices del triángulo) y se quiere establecerse una estación de servicio en el medio de tal manera que se encuentre a la misma distancia de las rutas que las unen. Dado el triángulo buscar el incentroa partir de las propiedadesEl ejemplo lo tome prestado del foro. su autora es Saint Lary, Yesica Andrea

11. ColonEstación de servicioSan JoséVilla Elisa

12. Teorema de Pitagoras

13. El lado más largo del triángulo se llama "hipotenusa", así que la definición formal es:En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (llamamos "triángulo rectángulo" a un triángulo con un ángulo recto) Teorema de PitágorasEl lado más largo del triángulo se llama "hipotenusa", así que la definición formal es:En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (llamamos "triángulo rectángulo" a un triángulo con un ángulo recto)

14. Ejemplo. Un triángulo de lados "3,4,5" tiene un ángulo recto, Veamos si las áreas son la misma:32 + 42 = 52Calculando obtenemos:9 + 16 = 25

29. Este trabajo es una recopilación de los trabajos presentados en el foroDel Taller de Geometría- del programa: