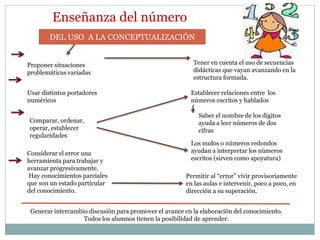
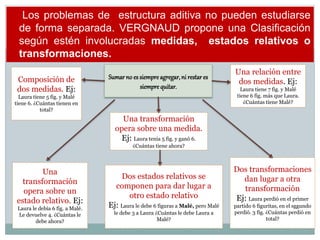
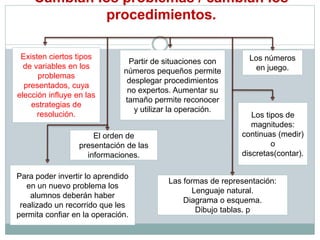
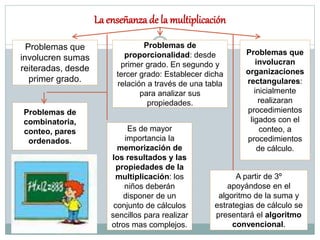
El documento presenta orientaciones didácticas para la enseñanza de los números y operaciones en la educación primaria, enfatizando la importancia de abordar el error como una oportunidad de aprendizaje y el uso de secuencias didácticas. Se destacan diversas estrategias para la resolución de problemas, incluyendo el cálculo mental y el uso de calculadoras, y se subrayan los conceptos de suma, resta, multiplicación y división, junto con sus aplicaciones en contextos reales. Se propone fomentar espacios de discusión activa en el aula, donde tanto las respuestas correctas como las incorrectas se analicen para promover un aprendizaje significativo.

1. NÚMEROS Y OPERACIONES
EN EL PRIMER CICLO.
Orientaciones didácticas
para el trabajo en el aula

2. Enseñanza del número
DEL USO A LA CONCEPTUALIZACIÓN
Proponer situaciones
problemáticas variadas
Usar distintos portadores
numéricos
Comparar, ordenar,
operar, establecer
regularidades
Considerar el error una
herramienta para trabajar y
avanzar progresivamente.
Hay conocimientos parciales
que son un estado particular
del conocimiento.
Tener en cuenta el uso de secuencias
didácticas que vayan avanzando en la
estructura formada.
Establecer relaciones entre los
números escritos y hablados
Saber el nombre de los dígitos
ayuda a leer números de dos
cifras
Los nudos o números redondos
ayudan a interpretar los números
escritos (sirven como apoyatura)
Permitir al “error” vivir provisoriamente
en las aulas e intervenir, poco a poco, en
dirección a su superación.
Generar intercambio discusión para promover el avance en la elaboración del conocimiento.
Todos los alumnos tienen la posibilidad de aprender.

3. Los problemas de estructura aditiva no pueden estudiarse
de forma separada. VERGNAUD propone una Clasificación
según estén involucradas medidas, estados relativos o
transformaciones.
Sumar no es siempre agregar, ni restar es
siempre quitar.
Composición de
dos medidas. Ej:
Laura tiene 5 fig. y Malé
tiene 6. ¿Cuántas tienen en
total?
Una transformación
opera sobre una medida.
Ej: Laura tenia 5 fig. y ganó 6.
¿Cuántas tiene ahora?
Una relación entre
dos medidas. Ej:
Laura tiene 7 fig. y Malé
tiene 6 fig. más que Laura.
¿Cuántas tiene Malé?
Dos transformaciones
dan lugar a otra
transformación
Ej: Laura perdió en el primer
partido 6 figuritas, en el sggundo
perdió. 3 fig. ¿Cuántas perdió en
total?
Una
transformación
opera sobre un
estado relativo. Ej:
Laura le debía 6 fig. a Malé.
Le devuelve 4. ¿Cuántas le
debe ahora?
Dos estados relativos se
componen para dar lugar a
otro estado relativo
Ej: Laura le debe 6 figuras a Malé, pero Malé
le debe 3 a Laura ¿Cuántas le debe Laura a
Malé?

4. Cambian los problemas / cambian los
procedimientos.
Existen ciertos tipos
de variables en los
problemas
presentados, cuya
elección influye en las
estrategias de
resolución.
Partir de situaciones con
números pequeños permite
desplegar procedimientos
no expertos. Aumentar su
tamaño permite reconocer
y utilizar la operación.
Para poder invertir lo aprendido
en un nuevo problema los
alumnos deberán haber
realizado un recorrido que les
permita confiar en la operación.
Los números
en juego.
Los tipos de
magnitudes:
continuas (medir)
o
discretas(contar).
El orden de
presentación de las
informaciones.
Las formas de representación:
Lenguaje natural.
Diagrama o esquema.
Dibujo tablas. p

5. ESTRATEGIAS DE CÁLCULO
 El aprendizaje de las diversas estrategias de cálculo incluye muchos otros aspectos.
Además del dominio del algoritmo se plantea la enseñanza del “cálculo
reflexionado”.
 En el proceso de aprendizaje de las operaciones, los alumnos deben tener la
posibilidad de: estimar previamente, controlar posteriormente los resultados, utilizar
diversos procedimientos de cálculo, tomar decisiones para un cálculo aproximado o
exacto.
 Se enfoca la enseñanza del cálculo mental: Conjunto de procedimientos no
algorítmicos. Estos se apoyan en las propiedades del sistema de numeración y de
las operaciones.
 Se puede resolver problemas aun cuando no se haya aprendido un algoritmo.
 Para hacer cálculos mentales hace falta disponer de algunos conocimientos.

6. El uso de la calculadora
PLANTEAR PROBLEMAS
DONDE SE UTILICE EL
CÁLCULO MENTAL EN
VARIADAS SITUACIONES.
DEBE SER UTILIZADA PARA
INVESTIGAR RELACIONES
ENTRE NÚMEROS Y ADEMÁS
PARA CONTROLAR Y
CORREGIR EL RESULTADO DE
LAS CUENTAS.

7. La enseñanza de la multiplicación
Problemas que
involucren sumas
reiteradas, desde
primer grado.
Problemas de
proporcionalidad: desde
primer grado. En segundo y
tercer grado: Establecer dicha
relación a través de una tabla
para analizar sus
propiedades.
Problemas que
involucran
organizaciones
rectangulares:
inicialmente
realizaran
procedimientos
ligados con el
conteo, a
procedimientos
de cálculo.
Problemas de
combinatoria,
conteo, pares
ordenados.
Es de mayor
importancia la
memorización de
los resultados y las
propiedades de la
multiplicación: los
niños deberán
disponer de un
conjunto de cálculos
sencillos para realizar
otros mas complejos.
A partir de 3º
apoyándose en el
algoritmo de la suma y
estrategias de cálculo se
presentará el algoritmo
convencional.

8. La enseñanza de la división ( lo que sobra
no siempre se reparte)
 Los niños podrán resolver problemas a través del conteo, del reparto uno a
uno, de sumas y restas.
 Producir una estrategia propia de resolución a partir de lo que saben.
 Las particiones no siempre son muy justas. Proponer situaciones de
particiones no equitativas y otras que exijan una distribución en partes iguales.
Repartos equivalentes.
 No es lo mismo repartir que averiguar las partes.
 A veces lo que sobra cambia todo el problema. Este tipo de problema permite
poner en juego el análisis del resto.
 Problemas de proporcionalidad. No todos los problemas de división son
problema de reparto.
 Problemas de organizaciones rectangulares.
 Diversos problemas para construir los significados de división.

9. ORGANIZAR ESPACIOS DE DISCUSIÓN
La act ividad por parte del alumno debe haber
sido “ g e n u i n a ” para poder ref lexionar sobre el la.
La intervención del docente debe ser variada y
centrada en el objet ivo de enseñanza.
Aceptar las respuestas correctas así como las
incorrectas .
Formular algunas expl icaciones para que
comprenda “ t o d o ” el grupo. Cuidar que toda la
clase comprenda.
Pedir just i f icaciones . Encontrar semejanzas y
di ferencias .
Tomar como objeto de discusión las soluciones
erróneas .
Promover la apropiación de procedimientos mas
económicos y conf iables en forma progresiva.

10. ESPACIOS DE DISCUSIÓN
Abrir, guiar y
sostener estos
momentos en las
clases.
Es un modelo costoso y
genera incertidumbre
pero es el camino
inevitable en la
construcción de los
conocimientos.
Espacios
indispensables de los
procesos didácticos
como herramientas
para ayudar a los
alumnos en su
aprendizaje.

11. “Paso a paso y acabadamente”
debe ser sustituido por
“compleja y provisoriamente”.
MAESTRA DE APOYO: SANDRA NAVARRO