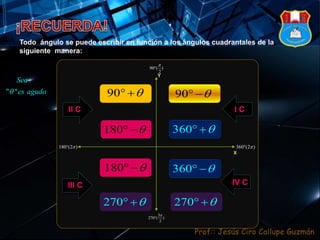
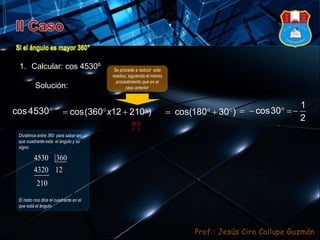
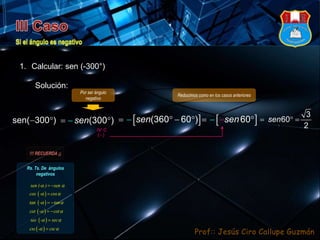
1) El documento explica cómo se pueden escribir cualquier ángulo en función de los ángulos cuadrantales de 90°, 180° y 270° mediante la adición o sustracción de múltiplos de 360°. 2) Además, muestra cómo reducir los ángulos resultantes a su forma canónica mediante división entre 360° y considerando el cuadrante y signo apropiados. 3) Finalmente, presenta fórmulas para trabajar con ángulos negativos.

1. Prof:: Jesús Ciro Callupe Guzmán

2. Prof:: Jesús Ciro Callupe Guzmán
X
Y
360 (2 )
90 ( )
2


180 (2 )
3
270 ( )
2


Todo ángulo se puede escribir en función a los ángulos cuadrantales de la
siguiente manera:
90  
360  
90  
180  
180  
270  
360  
270  
II C
III C
I C
IV C
:
" "
Sea
es agudo

3. Prof:: Jesús Ciro Callupe Guzmán
Pueden ser reducidos siguiendo el siguiente esquema:
180
. .
180
RT


 
 
 
90
. .
270
RT


 
 
 
 . .( )RT 
. . .( )Co RT 

4. Prof:: Jesús Ciro Callupe Guzmán
Se busca el cuadrante al que
pertenece el ángulo y el signo
que debe llevar.
1. Calcular: tan 300º
Solución:
Escribimos al ángulo en
función al ángulo cuadrantal
(360°-).
tan300    tan(360 60 )   tan60 3
Reducir siguiendo la siguiente relación:
180
. . . .( )
180
RT RT



 
  
 
( )
IV C
Se busca el cuadrante al que
pertenece el ángulo y el signo
que debe llevar.
2. Calcular: sen 240º
Solución:
Escribimos al ángulo en
función al ángulo cuadrantal
(360°-).
240sen    (270 30 )sen    
3
cos30
2
Reducir siguiendo la siguiente relación:
90
. . . .( )
270
RT Co RT



 
   
 
( )
III C

5. Prof:: Jesús Ciro Callupe Guzmán
1. Calcular: cos 4530º
Solución:
Se procede a reducir este
residuo, siguiendo el mismo
procedimiento que en el
caso anterior.
cos4530    cos(360 12 210 )x    cos(180 30 )
Dividimos entre 360 para saber en
que cuadrante esta el ángulo y su
signo.
El resto nos dice el cuadrante en el
que está el ángulo .
4530 360
4320 12
210
   
1
cos30
2
( )
III C

6. Prof:: Jesús Ciro Callupe Guzmán
1. Calcular: sen (-300°)
Solución:
Por ser ángulo
negativo
 sen( 300 )   (300 )sen      (360 60 )sen   
3
60
2
sen
( )
IV C
Rs. Ts. De ángulos
negativos
 )
 )
 )
 )
 )
sen (- ) sen
cos - cos
tan - tan
cot - cot
sec - sec
csc - csc
 
 
 
 
 
 
 

 
 


   60sen
!!! RECUERDA ¡¡
Reducimos como en los casos anteriores